МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––

Казанский государственный энергетический университет

Утверждено учебным управлением КГЭУ

Р.А.Ишмуратов

Методические указания к самостоятельной работе по курсу

“Преобразование измерительных сигналов”

Казань 2004

2

УДК 621.37 ББК 32.811.3 И 97

Ишмуратов Р.А. Методические указания к самостоятельной работе по курсу «Преобразование измерительных сигналов». Казань: Казан. гос. энерг.

ун-т, 2004.

Приведен перечень индивидуальных заданий для самостоятельного выполнение студентами типового расчета по курсу «Преобразование измерительных сигналов». Темой типового расчета выбрано аналитическое вычисление спектра заданного периодического сигнала и обратное восстановление сигнала по конечному числу гармоник с использованием вычисленных коэффициентов ряда Фурье.

Операции спектрального разложения и последующего синтеза сигнала широко используются при цифровой обработке сигналов. В данных методических указаниях приведено краткое изложение теории по рассматриваемой теме и подробный пример выполнения одного варианта расчетного задания. Данный типовой расчет служит для проверки знаний и освоения навыков проведения как аналитических выкладок, так и практического моделирования на компьютере. В предлагаемом расчетном задании компьютерное моделирование предполагает знание студентами одного из универсальных языков программирования, таких как QBasic или Visual Basic, в объеме не превышающей стандартной вузовской программы ГОС по курсу «Информатика». Для удобства выполнения заданий в Приложениях 1 и 2 приведены основные обозначения и полезные тригонометрические формулы. В Приложении 3 приведены варианты заданий для индивидуального выполнения.

Данные методические указания предназначены для студентов специальности «Информационно-измерительная техника и технологии» и служат дополнением к лекционному курсу «Преобразование измерительных сигналов».

________________

© Казанский государственный энергетический университет, 2004

3

Цель работы

Целью работы служит ознакомление студентов с такими понятиями «Теории сигналов», как ряд Фурье и спектр периодического сигнала, восстановление (синтез) сигнала по конечному числу составных гармоник сигнала, эффект Гиббса. Работа помогает получению навыков аналитического вычисления коэффициентов ряда Фурье, способности проведения модельных расчетов с использованием универсальных языков программирования. Операции спектрального разложения и последующего синтеза сигнала широко используется при цифровой обработке сигналов.

Краткое изложение теории по теме

Любой сигнал – это некоторая функция от времени s(t). Если сигнал s(t) периодический с периодом T (рис.1), то для полного математического описания сигнала нам достаточно знание сигнала на интервале одного периода [0,

T] (или [–T/2, T/2] ).

τи

A

t

T

Рис.1. Пример периодического сигнала

Из математики известно, что любую периодическую функцию, т.е. функцию, заданную на интервале периода, можно разложить в ряд Фурье

где ωk = k ω0 , ω0 = 2π/T – основная частота ряда (иногда в литературе основная частота записывается также как ω1, имея в виду, что это первая гар-

Таким образом, любой периодический сигнал можно представить как сумму постоянной составляющей и бесконечную сумму гармонических сигналов (гармоник) с частотами ωk = k ω0 , k = 1, 2, 3,… , кратными основной частоте ряда ω0. Каждая k-я гармоника представляет собой сумму синусного и косинусного колебаний. Например, 1-я гармоника – это сумма двух гармонических колебаний с одинаковой частотой ω0 и амплитудами a1 и b1 , 2-я

гармоника – с частотой ω2 и амплитудами a2 и b2 и т.д.

1-я гармоника: a1 cos ω0t + b1 sin ω0t , 2-я гармоника: a2 cos ω2t + b2 sin ω2t , 3я гармоника: a3 cos ω3t + b3 sin ω3t и т. д.

Каждую гармонику можно представить другим способом (это следует из тригонометрических соотношений) – как одно гармоническое колебание (синусоиду или косинусоиду) с некоторой амплитудой Ak и начальной фазой ϕk

Поскольку, как известно из тригонометрии, арктангенс угла всегда лежит в диапазоне от –π/2 , до π/2 , для правильного восстановления фазы необходимо провести дополнительные преобразования:

Итак, любой периодический сигнал можно представить как сумму бесконечного числа составных гармоник с частотами, кратными основной частоте ряда ω0. Каждую k-ю гармонику ряда можно представить двумя способами: как сумму двух гармонических колебаний – синусного и косинусного, или как одно гармоническое колебание с амплитудой Ak и начальной фазой ϕk . Распределение амплитуд Ak по номерам гармоник называют амплитудной спектральной диаграммой периодического сигнала или просто амплитудным спектром сигнала, а график зависимости ϕk от номеров гармоник – фазовой спектральной диаграммой или фазовым спектром. Для иллюстрации на рис.2 приведен пример амплитудного и фазового спектров некоторого периодического сигнала.

Ak ϕk

A1

A2A3

a0

2

Рис.2. Амплитудный (а) и фазовый (б) спектры некоторого периодического сигнала

6

Пример вычисления спектра для прямоугольного сигнала

Найдем амплитудный спектр (в дальнейшем просто спектр) сигнала, представляющего собой последовательность однополярных прямоугольных импульсов с длительностью импульсов τ, периодом T и амплитудой U (рис.3). Скважность импульсов q = T / τ .

s(t)

U

T

Рис.3. Последовательность однополярных прямоугольных импульсов

Решение

Так как сигнал периодический, то он полностью задан на интервале [0, T] (или [–T/2, T/2 ] ). Поскольку сигнал (импульс) симметричный, поместим ось ординат по центру импульса (рис.4). В результате мы получим четную функцию, отличную от нуля на интервале [–τ/2, τ/2 ] .

s(t)

U

Рис.4. Сдвиг оси ординат для центрированного расположения симметричного импульса

Математическое описание данного сигнала:

7

+Вычисляем коэффициенты ряда Фурье (2):

В последней формуле bk = 0 поскольку s(t) – это четная функция, а си-

нус – нечетная функция, следовательно интеграл произведения этих функций равен нулю.

Подставляя теперь формулы, полученные для коэффициентов a0 , ak и bk в формулу (1), и задаваясь определенным количеством гармоник

k = 1,… M , мы получим искомый синтезированный сигнал sсинт(t). Точность приближения sсинт(t) к s(t) будет зависеть от значения M : чем больше M, тем точнее приближение. При этом восстановленный сигнал будет испытывать небольшие волнообразные флуктуации. Эти небольшие искажения сигнала есть следствие ограниченного количества гармоник при суммировании (эффект Гиббса).

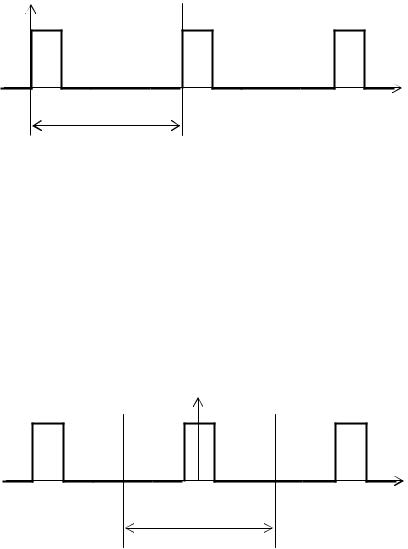
Результаты проведенного на компьютере моделирования (копия экрана монитора) прямоугольного сигнала для скважности q = 2 при различном количестве M составных гармоник, участвующих в синтезе сигнала, представлены на рис.5. Из сравнения двух графиков видно, что действительно с увеличением M точность приближения синтезированного сигнала к заданному исходному виду возрастает. Волнообразные флуктуации кривой графика отражают эффект Гиббса, обусловленный конечным числом составных гармоник.

8

а)

б)

Рис.5. График восстановленного (синтезированного) прямоугольного сигнала (для скважности q = 2) при различном количестве M составных гармоник: (а)

– M = 11, (б) M = 31

В Приложении 1 для справки приведены обозначения основные переменных, а в Приложении 2 – основные тригонометрические формулы, необходимые при расчетах.

Задание на выполнение типового расчета

1. Дан периодический измерительный сигнал s(t) (конкретный вид сигнала задается преподавателем индивидуально для каждого студента – см. Приложение 3) с параметрами: амплитуда U, длительность импульса τ и скважность q.

9

2.Привести математическое описание заданного сигнала s(t).

3.Рассчитать аналитически амплитудный спектр – получить формулы для коэффициентов ряда Фурье a0 , ak и bk для заданного периодического

сигнала. Построить в тетради график амплитудного спектра сигнала до 10-й гармоники включительно.

4. Разработать программу моделирования синтеза измерительного сигнала по конечному числу составных гармоник M с использованием полученных формул для коэффициентов ряда Фурье. В разработанной программе предусмотреть вывод графика синтезированного сигнала на экран монитора.

При моделировании задаться следующими значениями параметров сиг-

нала:

U = 1, τ = 50, q = 2. Интервал времени задания сигнала t от 1 до N,

N = 500.

__________________

Литература

Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа.

2002.

10

Приложение 2

Полезные тригонометрические формулы

Основная пара соотношений – это формулы для синуса (косинуса) суммы и разности двух углов:

sin(α ±β) = sin α cosβ ± cos α sin β; cos(α ± β) = cos α cosβ m sin α sin β;

Из этой пары соотношений вытекают следующие дополнительные формулы:

sin 2α = 2 sin α cos α ;

cos 2α = cos2 α − sin 2 α;