diskretka

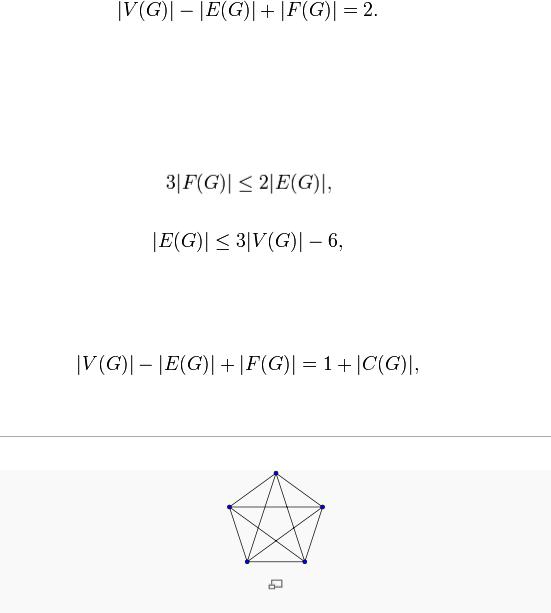
5) Планарность. Основные понятия.

Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер.

Граф называется планарным, если он изоморфен некоторому плоскому графу.

Т. Понтрягина-Куратовского.

Формула Эйлера

Для связного плоского графа справедливо следующее соотношение между количеством вершин , ребер и граней (включая внешнюю грань):

Оно было найдено Эйлером в 1736 г.[1] при изучении свойств выпуклых многогранников. Это соотношение справедливо и для других поверхностей с

точностью до коэффициента, называемого эйлеровой характеристикой. Это инвариантповерхности, для плоскости или сферы он равен двум. Формула

имеет множество полезных следствий. Если каждая грань ограничена не менее чем тремя ребрами (при условии, что в графе больше двух ребер), а каждое ребро разделяет две грани, то

следовательно,

то есть, при большем числе ребер такой граф заведомо непланарен. Обратное утверждение не верно, например, граф Петерсена. Отсюда следует, что в планарном графе всегда можно найти вершину степени не более 5.

Общая формула также легко обобщается на случай несвязного графа:

где — количество компонент связности в графе. [править]Два примера непланарных графов

[править]Полный граф с пятью вершинами

K5, полный граф с 5 вершинами

Лемма. Полный граф с пятью вершинами (К5) нельзя уложить на плоскость.

Доказательство. Для него не выполняется .

[править]«Домики и колодцы»

Граф «домики и колодцы» (K3,3)

Задача о тр х колодцах. Есть три дома и три колодца. Можно ли так проложить дорожки между домами и колодцами, чтобы от каждого дома к каждому колодцу вела дорожка, и никакие две дорожки не пересекались бы. Мосты строить нельзя.

Лемма. Полный двудольный граф с тремя вершинами в каждой из долей (К3,3) нельзя уложить на плоскость.

Доказательство. По формуле Эйлера граф имеет 5 граней.

С другой стороны: любая грань (включая внешнюю) содержит не менее 4 рёбер. Поскольку каждое ребро включается в ровно две грани, получается соотношение , F — количество граней, E — количество рёбер. Подставляем в это неравенство F=5 и E=9 и видим, что оно не выполняется.

Теорема Понтрягина-Куратовского

В общем случае найти K5 или K3,3 довольно сложно. На первый взгляд кажется, что граф Петерсена содержит K5. Оказывается, нет — в нём есть подграф, стягивающийся в K3,3.

Очевидно утверждение: если граф G содержит под-

граф, гомеоморфный K5 или K3,3, его невозможно разложить на плоскости. Оказывается, верно и обратное.

Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных полному графу из пяти вершин (K5) или

графу «домики и колодцы» (K3,3).

Теорему также можно сформулировать в следующем варианте (иногда его называют «теорема Вагнера»).

Граф планарен тогда и только тогда, когда не содержит подграфов, стягивающихся в K5 или K3,3.

6 Раскраски. Основные понятия.

Хроматическое число

графа называется отображение множества вершин графа на конечное множество (множество цветов); n-раскраска графа - раскраска с использованием n цветов. Раскраска называется правильной, если никакие две вершины одного цвета не смежны. Очевидно, что для графа без петель всегда существует правильная раскраска в |V| цветов.

Хроматическим числом графа G называется минимальное число n=c(G), такое, что существует правильная n-раскраска.

. Т. о пяти красках.

Теорема о пяти красках.

Каждый планарный граф без петель и кратных ребер является не более чем 5- хроматическим.

Гипотеза четырех красок.

Теорема о четырех красках.

Каждый планарный граф без петель и кратных ребер является не более чем 4- хроматическим.

7 Критические графы.