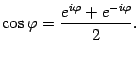№1

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей

Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу, а коэффициент при мнимой части – ординату точки.

Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.

На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi, где y № 0 – точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной.

№2

Тригонометрическая форма записи комплексного числа.

   Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е.  и полярные , то они связаны соотношением (1):

                             .

По определению,  и из (1) получаем:

                             .                                   (9)

Подставляя в алгебраическую форму записи числа z получаем: . Или

                                             (10)

Определение. Запись комплексного числа в виде (3) называется еготригонометрической формой.

Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:

                          ,                                (11)

где .

Теорема. (О равенстве комплексных чисел в тригонометрической форме.)

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.

   Доказательство. Так как между всеми комплексными числами и всемиточками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.

Теорема доказана.

   Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.

   Пусть , т.е. , . Тогда

                                    ,                               (12)

, если точка z лежит в первой или четвертой четверти или , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где .

Пример. Найти тригонометрическую форму записи комплексного числа z, если:

а) ;  б) ;  в) ;  г) ;  д) .

Решение. а) , .

 , .

Ответ: .

б) , , , .

Ответ: .

в) , , , .

Ответ: .

г) , , , .

Ответ: .

д) , , ,

.

Ответ: , где .

Замечание. В некоторых случаях удобнее не пользоваться формулами, а изображать на чертеже соответствующую точку на комплексной плоскости и находить модуль и аргумент комплексного числа пользуясь чертежом. Например, найдем тригонометрическую форму комплексного числа .

   Число  соответствует на комплексной плоскости точке . Отметим ее на координатной плоскости:

                    

                                       рис.5.

   Из рис.5 мы сразу же видим, что  и . Отсюда, .

Найдем, далее тригонометрическую форму числа комплексно сопряженного числу , т.е. .

Из рис.5 мы видим, что ,  и

 или .

   Замечание. Несмотря на то, что , а , форма записи комплексного числа z с аргументом  в виде  не является тригонометрической, т.к. . В этом случае правильной записью тригонометрической формы комплексного числа будет:

 или .

Умножение комплексных чисел в тригонометрической форме записи. Свойства модуля комплексных чисел.

Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)

 Пусть , где  и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

.                 (13)

   Доказательство. 

, ч.т.д.

Теорема доказана.

Отсюда вытекает правило умножения комплексных чисел в тригонометрической форме записи.

Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи нужно перемножить их модули, а аргументы сложить.

Следствие 1. Пусть k натуральное число и . Пусть далее , где  – произвольные n комплексных чисел записанных в тригонометрической форме записи. Тогда

.

   Доказательство проводится индукцией по числу сомножителей и предоставляется читателю.

Следствие 2. Пусть n натуральное число и  – произвольное комплексное число в тригонометрической форме записи. Тогда

.

   Доказательство сразу же следует из Следствия 1.

Теорема. (Свойства модуля комплексного числа.)

Пусть  – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:

1)  и . Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;

2) расстояние между точками  и  комплексной плоскости равно модулю разности соответствующих комплексных чисел:  ;

3) ;

4) ;

   Доказательство. 1) По предыдущей теореме имеем:

, где  и ,

т.е. .

   Таким образом, равенства  и  есть тригонометрическая форма записи числа , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем , ч.т.д.

   Далее, т.к. , то по только что доказанному свойству , ч.т.д.

   Заметим, что последнее равенство можно получить и из других соображений.

   Противоположные числа на комплексной плоскости изображаютсяточками симметричными относительно начала координат. Действительно, пусть . Тогда  и точки ,  имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е. , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.

2). Пусть , . Тогда  и по формуле (12) имеем:

            .                      (14)

   С другой стороны, рассмотрим числа  и  как точки на комплексной плоскости. Тогда точка  имеет декартовые координаты ,  а  и искомое расстояние между ними вычисляется по формуле (14), ч.т.д.

3) Рассмотрим на комплексной плоскости точки ,  и начало координат О. В общем случае эти три точки являются вершинами треугольника :

                      

                                          рис.6.

   Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.

   Мы только что доказали, что длина стороны  этого треугольника равна , а длины сторон  и  равны по определению модулям чисел  и : , . Отсюда и получаем, что .

   Заменим в последнем  неравенстве число  на противоположное число , тогда получаем:

, ч.т.д.

   Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда треугольник вырождается в отрезок прямой, т.е. когда все три точки О,  и  лежат на одной прямой.

4) , откуда следует

. Поменяв местами  и , получаем

, откуда и следует доказываемое неравенство.

Теорема доказана.

   Теория комплексных чисел имеет много приложений в различных областях математики. Не могу удержаться от искушения привести хотя бы один такой пример, относящийся к области теории чисел.

Определение. Говорят, что натуральное число n представимо в виде суммы двух квадратов, если существуют такие целые числа х и у, что выполняется равенство:

                                       .

Теорема. Если два числа представимы в виде суммы двух квадратов, то их произведение также представимо в виде суммы двух квадратов.

   Доказательство. Пусть  и , где .

   Нам нужно доказать, что найдутся два целых числа а и b такие, что .

   С этой целью рассмотрим два комплексных числа  и .

   Тогда  и по формуле (12) имеем: .

   С другой стороны, , . Так как , то  или , то отсюда получаем равенство: , где , ч.т.д.

Теорема доказана.

Деление комплексных чисел в тригонометрической форме записи.

Теорема. (О делении комплексных чисел в тригонометрической форме)

Пусть , где  и , где  – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

             .                (2)

   Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:

 

, ч.т.д.

Пример 1. Запишите комплексные числа  и  в тригонометрической форме и найдите их произведение  и частное .

Решение. 1) Комплексное число  на комплексной плоскостинаходится во второй четверти, поэтому

, .

2) Комплексное число  на комплексной плоскости находится во четвертой четверти, поэтому

, .

3) 

.

Ответ: , .

Пример 2. Вычислить .

Решение. Комплексное число  на комплексной плоскостинаходится в третьей четверти, поэтому , 

Применим формулу Муавра:

.

№3

Два комплексных числа a + b•i и a - b•i называются сопряженными. Сопряженные комплексные числа в сумме дают действительное число2a

Свойства комплексно сопряженных чисел.

1.   .

2.  .

3.   .

4.  .

5.   

6.  .

7.  .

8.  

9. Для любого многочлена  с действительными коэффициентами от комплексной переменной z

    .

Доказательство. 1) Пусть  – произвольное комплексное число. Тогда по определению комплексно сопряженного числа  и , ч.т.д.

2) Пусть . Тогда  и . С другой стороны,  и , откуда и следует, что .

3) Докажем с помощью метода математической индукции, что равенство  верно для любого числа слагаемых n.

а) База индукции.

При ,  равенство   только что доказано.

б) Индукционная гипотеза.

Предположим, что утверждение верно, если число слагаемых равно :.

в) Индукционный переход.

Так как утверждение верно для двух слагаемых, то

. Далее используем индукционное предположение:

, откуда и следует доказываемое равенство.

4) Пусть . Тогда  и . С другой стороны, , откуда и следует, что .

5) Доказывается аналогично пункту 3) методом математической индукции.

6) Пусть  и k – произвольное натуральное число. Тогда по определению натуральной степени числа , ч.т.д.

7) Пусть а – действительное число. Тогда  и по определению комплексно сопряженного числа , ч.т.д.

8) Пусть . По уже доказанным в пунктах 4) и 7) свойствах  , ч.т.д.

9) Пусть z – комплексная переменная и  – многочлен от комплекснойпеременной z с действительными коэффициентами:, где

– действительные числа. Тогда, используя уже доказанные свойства, получаем:

, ч.т.д.

Теорема доказана.

Пример. Вычислить .

Решение. Обозначим . Тогда , , . Отсюда, .

№4

Формула Эйлера устанавливает взаимосвязь между экспоненциальной функцией  мнимого аргумента с одной стороны и тригонометрическими функциями  и  - с другой:   (1)         Доказательство формулы Эйлера основано на разложении вышеуказанных функций в ряд Тейлора:   (2)     (3)     (4)         Преобразуем формулу (2), выполнив подстановку :   (5)         Перегруппируем слагаемые, выделив вещественную и мнимую части:   (6)         В соответствии с формулами(3) и (4) вещественная часть функции  exp(iφ)  равна  cos φ, а мнимая часть этой функции равна sin φ. Следовательно,   (7)   что и устанавливает формула Эйлера.       Формула Эйлера позволяет обобщить понятие показательной функции вещественного аргумента на случай его комплексных значений:   (8)         Отметим, что показательные функции с комплексными и вещественными степенями имеют одинаковые свойства:   (9)     (10)     (11)

Извлечение корня из комплексного числа

Заголовок этого раздела является не совсем точным. Дело в том, что корень из ненулевого комплексного числа однозначно определить нельзя. Он всегда имеет столько значений, какова его степень. Поэтому в данном разделе мы будем говорить о решении уравнения

(17.14)

где неизвестным служит  , а   -- известное комплексное число. Но поскольку в школе решение этого уравнения записывалось в виде  , то, не слишком соблюдая математическую строгость, можно говорить, что мы будем извлекать корень  -ой степени из комплексного числа  . Итак, решаем уравнение (17.14).

Если  , то  . Пусть  . Запишем число  в тригонометрической форме:  . Здесь  и   -- известные величины. Запишем неизвестное число  в тригонометрической форме:  . Здесь  и   -- неизвестны. По формуле Муавра

Таким образом,

Если два комплексных числа равны, то их модули должны быть равны. Поэтому  . В этом соотношении  и   -- положительные числа, следовательно  , где справа стоит обычный арифметический корень из положительного числа.

Если два комплексных числа равны, то аргументы у них могут различаться только на величину, кратную  . Поэтому  ,  . Отсюда находим, что

В итоге получили:

(17.15)

Значения  , отличные от указанных в этой формуле, дадут те же значения  , которые можно получить при 

        Пример 17.9   Найдите корни уравнения  .

Решение. Запишем число  в тригонометрической форме:

то есть  ,  . Тогда

При  получим:

При  получим:

При  получим:

При  получим:

Ответ:  ,  ,  ,  .     

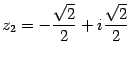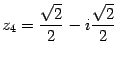№5

Показательная форма комплексного числа

Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой

(17.10)

которая носит название формулы Эйлера. Обосновать ее можно с помощью теории степенных рядов. Эта теория будет изложена в курсе математического анализа.

Пусть комплексное число  в тригонометрической форме имеет вид  . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим

Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь  ,  .

        Пример 17.7   Пусть  . Напишите показательную форму числа  .

Решение. Находим модуль и аргумент числа:

Следовательно, показательная форма комплексного числа такова:

        

        Пример 17.8   Комплексное число записано в показательной форме

Найдите его алгебраическую форму.

Решение. По формуле Эйлера

Итак, алгебраическая форма числа:  .         

С помощью формулы Эйлера можно определить показательную функцию комплексного аргумента. Пусть  . Тогда

Например,

Заменим в формуле Эйлера  на  . Получим:

С учетом свойств тригонометрических функций имеем:

Сложив последнюю формулу с формулой Эйлера, получим:

Откуда

(17.11)

Аналогично, с помощью вычитания, можно получить формулу

(17.12)

С помощью формулы для косинуса вычислим, например,  :

Таким образом, в комплексной области модуль косинуса может быть и больше 1. Более того, в комплексной области функции  и  , определяемые с помощью формул (17.11) и (17.12), являются неограниченными функциями. Действительно, из этих формул мы получаем:

(17.13)

Так как гиперболические косинус и синус являются неограниченными функциями, то и тригонометрические функции косинус и синус являются неограниченными функциями (в комплексной области).

Отметим также, что формулы (17.13) объясняют, почему для гиперболических функций многие соотношения очень похожи на соотношения между тригонометрическими функциями, например, основное тригонометрическое тождество, формулы двойного аргумента.

№6

Вектор — это элемент векторного пространства (некоторого множества с двумя операциями на нём, которые подчиняются восьми аксиомам). С точки зрения математики, после выбора базиса пространства, вектор представляет собой набор величин (координат вектора), которые меняются строго определённым образом при изменении базиса и системы координат, причём изменившиеся величины полагаются координатами того жесамого вектора в новом базисе и новой системе координат. Благодаря этому свойству вектор представляет собой объект, не зависящий от выбора базиса и связанной с ним системы координат. Точнее, координаты вектора являются разновидностью тензора — это тензор первого ранга типа (1,0).

Два вектора называются равными, если они:

1. коллинеарны

2. равны по длине

3. одинаково направлены

Или же — если они имеют одинаковые координаты в некотором (и тогда любом) базисе.

Операции над векторами

В этом разделе мы вспомним известные из школьного курса математики операции сложения векторов и умножения вектора на число, а также свойства этих операций.

        Определение 10.6   Суммой векторов a и b называется такой третий вектор c, что при совмещенных началах этих трех векторов, векторы a и b служат сторонами параллелограмма, а вектор c -- его диагональю (рис. 10.2).         

Рис.10.2.Сложение векторов

Сложение векторов в соответствии с рисунком 10.2 называется сложением по правилу параллелограмма. Однако бывает более удобным использовать для сложения правило треугольника, которое становится ясным из рисунка 1.3. Из того же рисунка видно, что результаты сложения по правилу параллелограмма и по правилу треугольника одинаковы.

Рис.10.3.Правило треугольника

        Определение 10.7   Вектор b называется противоположным вектору a, если a и b коллинеарные, имеют противоположные направления и  .         

Вектор, противоположный вектору a, обозначается  , то есть  .

        Определение 10.8   Разностью векторов a и b называется сумма  .         

Разность обозначается  , то есть  . 

        Определение 10.9   Произведением вектора a на вещественное число  называется вектор b, определяемый условием

1)   и, если  , то еще двумя условиями:

2) вектор b коллинеарен вектору a;

3) векторы b и a направлены одинаково, если  , и противоположно, если  .         

Произведение вектора a на число  обозначается  (рис 1.4).

Рис.10.4.Умножение вектора на число

        Замечание 10.1   Когда речь идет о связи векторов с числами, то иногда числа называют скалярами. Таким образом,  определение 10.9 задает умножение вектора на скаляр.         

Рассмотрим некоторые свойства операций сложения и умножения вектора на число. Часть из них, которые будут особенно важны при обобщении понятия вектора, выделим в отдельную теорему.

        Теорема 10.1   Для любых векторов  и любых вещественных чисел  выполняются следующие свойства:  1)  (свойство коммутативности операции сложения);  2)  (свойство ассоциативности операции сложения);  3)  ;  4)  ;  5)  (свойство ассоциативности по отношению к числам);  6)  (свойство дистрибутивности по отношению к умножению на число);  7)  (свойство дистрибутивности по отношению к умножению на вектор;  8)  .

        Доказательство.     Свойство 1 следует из того, что при сложении векторов по правилу параллелограмма (рис. 10.2) порядок слагаемых не влияет на построение параллелограмма. Доказательство свойства 2 следует из рисунка 10.5.

Рис.10.5.Ассоциативность сложения

Свойства 3 и 4 очевидны при сложении векторов по правилу треугольника.

Докажем свойство 5. Векторы, стоящие в обеих частях доказываемого равенства, имеют одинаковую длину  . Если это произведение равно нулю, то векторы в правой и левой частях доказываемого равенства нулевые и, следовательно, равны друг другу. В противном случае векторы  и  коллинеарны вектору a и имеют с ним одинаковое направление, если числа  и  одного знака, и направление, противоположное вектору a, если  и  разного знака. Следовательно,  .

Свойство 6 очевидно, если  . Если  и векторы a и b неколлинеарны, то это свойство вытекает из подобия треугольников на рисунке 10.6.

Рис.10.6.Свойство дистрибутивности

Случаи, когда  или a и b коллинеарны, предоставляем проанализировать читателю самостоятельно.

Для доказательства свойства 7 заметим, что векторы  и  коллинеарны. Без ограничения общности можно считать, что  (в противном случае поменяем местами  и  в доказываемом равенстве).

Пусть  и  одного знака. Тогда  ,  .

Пусть  и  имеют разные знаки. Тогда  ,  . Получили, что  в обоих случаях.

Векторы f и g имеют одно направление. Оно совпадает с направлением a при  и противоположно при  . Следовательно,  . Свойство 7 доказано.

Свойство 8 очевидным образом вытекает из  определения 10.9 произведения вектора на число.      

Из свойства ассоциативности следует, что в сумме векторов, содержащей три и более слагаемых, можно скобки не ставить. Как найти сумму нескольких слагаемых, не используя попарных сумм, видно из рисунка 10.7.

Рис.10.7.Сумма нескольких слагаемых

Сформулируем еще несколько очевидных свойств операций сложения и умножения вектора на число:  9) равенство  верно тогда и только тогда, когда или  , или  ;  10) вектор, противоположный вектору a, равен  , то есть  ;  11) для любых векторов a и b существует такой вектор x, что  .

№7

Основные сведения из векторной алгебры. Различают два рода величин: скалярные и векторные.

1. Если некоторая величина вполне определяется ее числовым значением, то ее называют скалярной. Примерами скалярных величин могут служить: масса, плотность, работа, сила тока, температура. Скаляры являются алгебраическими величинами и с ними можно производить любые алгебраические действия: сложение, вычитание, умножение, деление, возведение в степень и т. д.

2. Если при определении некоторой величины для ее полной характеристики, кроме числового значения, надо знать и ее направление, то такая величина называется векторной, или вектором. Примерами векторных величин являются скорость, ускорение, сила. Длина вектора называется также его модулем, или абсолютной величиной.

3. Вектор обозначается графически отрезком прямой, на котором ставится стрелка, указывающая направление вектора (см. рисунок).

Будем обозначать вектор одной буквой с черточкой над ней, например, , а модуль этого вектора - той же буквой, только без черточки над ней, т. е. a. Модуль вектора a часто обозначается .

Вектор будем также обозначать , где A - начало и B - конец вектора, а его модуль - теми же буквами, но без черточки наверху.

4. Вектор равен нулю, если его модуль равен нулю. Такой вектор называется нулевым.

5. Два вектора  и  называются равными, если: 1) равны их модули, 2) они параллельны и 3) направлены в одну и ту же сторону.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными. Вектор, противоположный вектору , обозначается через .

6. Сложение векторных величин производится по правилу параллелограмма: сумма двух векторов  и , приведенных к общему началу, есть третий вектор , длина которого равна длине параллелограмма, построенного на векторах  и , а направлен он от точки A к точке B (см. рисунок):

Модуль вектора  вычисляется по формуле

     (1)

7. Сумму нескольких векторов, например , ,  и , строят так: берут произвольную точку O плоскости и из нее строят вектор , равный вектору ; из точки A проводят вектор , равный вектору , из точки B - вектор , равный вектору  и, наконец, из точки C строят вектор , равный вектору . Вектор , замыкающий полученную ломаную линию OABCD, и будет суммой векторов , ,  и  (см. рисунок ниже):

По такому же правилу строится и сумма любого числа векторов.

8. Разностью двух векторов  и  называется такой третий вектор , который равен сумме векторов  и  (см. рисунок). Вектор  параллелен вектору , равен ему по модулю, но противоположно направлен:

9. При умножении вектора  на скаляр k получается вектор , модуль которого равен модулю вектора , умноженному на k, т. е.b = ak. Направления векторов  и  совпадают, если k > 0, и они противоположны, если k < 0. Имеем

, или .

10. Два вектора, лежащие на параллельных прямых, независимо от того, направлены они одинаково или противоположно, называются коллинеарными.

11. Единичным вектором, или ортом данного вектора, называется вектор, совпадающий по направлению с данным вектором и имеющий модуль, равный единице.

12. Проекцией вектора  на ось  называется длина отрезка A'B', заключенного между проекциями конца и начала вектора на эту ось. Этой длине приписывается знак плюс, если направление отрезка A'B' совпадает с направлением оси, и знак минус, если его направление противоположно направлению оси.

Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

Проекция вектора  на ось  обозначается через a_l или , а угол между осью  и вектором  будем обозначать так: . Таким образом,

     (2)

Если  - углы, образованные вектором  с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора  на координатные оси будут равны

     (3)

В дальнейшем предполагается, что система координат - прямоугольная.

Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле

     (4)

т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.

Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).

Если векторы  и  равны, то равны и их проекции:

a_1x = a_2x; a_1y = a_2y; a_1z = a_2z.     (5)

Если для вектора  известны координаты его начала A(x₁, y₁, z₁) и координаты его конца B(x₂, y₂, z₂), то проекции вектора  на координатные оси определяются по формулам

a_x = x₂ - x₁; a_y = y₂ - y₁; a_z = z₂ - z₁,     (6)

а модуль вектора в этом случае определится по формуле

     (7)

Очевидно, что по формуле (7) следует вычислять и расстояние между точками A(x₁, y₁, z₁) и B(x₂, y₂, z₂).

13. Проекция суммы векторов на какую-нибудь ось равна алгебраической сумме проекций этих векторов на ту же ось.

Из векторного равенства

     (8)

следуют такие три скалярные равенства:

a_x = a_1x + a_2x + a_3x + ... + a_nx;           a_y = a_1y + a_2y + a_3y + ... + a_ny;     (9) a_z = a_1z + a_2z + a_3z + ... + a_nz.          

14. Если  - векторы, по модулю равные единице и направленные по координатным осям Ox, Oy и Oz, то разложение вектора  по трем координатным осям выражается формулой

     (10)

где a_x, a_y и a_z - проекции вектора a на координатные оси - называются координатами вектора (если вектор  имеет координаты a_x, a_y,a_z, то это обозначается так: {a_x, a_y, a_z}). Если вектор  имеет начало в начале координат, а его конец A имеет координаты x, y и z, то тогда его проекции на координатные оси равны координатам его конца:

a_x = x; a_y = y; a_z = z.

В этом случае вектор  называется радиусом-вектором точки A. Радиус-вектор точки обозначается обыкновенно через  (см. рисунок):

     (11)

а модуль радиуса-вектора точки A(x, y, z) вычисляется по формуле

     (12)

15. Углы, образуемые вектором  с координатными осями Ox, Oy и Oz, определяются из формул (3) и (4):

           

     (13)

           

Косинусы, определяемые по этим формулам, называются направляющими косинусами вектора .

Для направляющих косинусов вектора имеет место формула

     (14)

т. е. сумма квадратов косинусов углов, образуемых вектором с тремя взаимно перпендикулярными осями, равна единице.

Если , т. е. если  - единичный вектор, обозначаемый обыкновенно , то его проекции на координатные оси вычисляются по формулам

     (15)

т. е. проекции единичного вектора  на оси прямоугольной системы координат Ox, Oy и Oz равны соответственно направляющим косинусам этого вектора. Имеет место формула

     (16)

16. Если даны два вектора

то 

и

     (17)

17. Скалярным произведением двух векторов  и  называется число, равное произведению их модулей на косинус угла между ними. Скалярное произведение векторов  и  обозначается символом . Если обозначить угол между векторами  и  через , для скалярного произведения будем иметь

     (18)

Из формулы (8) следует, что скалярное произведение двух векторов  и  - это произведение модуля одного из них на проекцию второго на направление первого вектора (см. рисунок):

     (19)

откуда .

Скалярное произведение двух перпендикулярных векторов равно нулю, так как в этом случае .

Скалярное произведение имеет свойства, аналогичные свойствам произведений чисел:

(переместительное свойство умножения);

(распределительное, или дистрибутивное свойство произведения).

Если векторы  и  заданы проекциями на координатные оси

то их скалярное произведение вычисляется по формуле

     (20)

а косинус угла  между этими векторами определяется по формуле

     (21)

Если углы, образуемые вектором  с координатными осями, обозначить через , а углы, образуемые вектором  с координатными осями, - через , то косинус угла  между векторами  и  определяется по формуле

     (22)

Если векторы  и  перпендикулярны, то их скалярное произведение равно нулю, и тогда

a_xb_x + a_yb_y + a_zb_z = 0,     (23)

или

     (24)

18. Векторным произведением векторов  и  называется вектор , который определяется следующими условиями:

1) Его модуль равен  где  - угол между векторами  и .

2) Вектор  перпендикулярен к плоскости, определяемой перемножаемыми векторами  и .

3) Вектор  направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы  и , кажется, что для кратчайшего совмещения первого сомножителя со вторым первый сомножитель нужно вращать против часовой стрелки (см. рисунок).

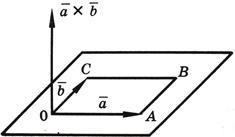
Векторное произведение векторов  и  обозначается символом :

     (25)

или

     (26)

Основные свойства векторного произведения:

1) Векторное произведение  равно нулю, если векторы  и  коллинеарны или какой-либо из перемножаемых векторов является нулевым.

2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):

Векторное произведение не обладает свойством переместительности.

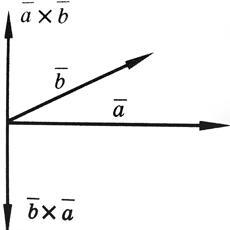
3)  (распределительное свойство).

Выражение векторного произведения  через проекции векторов  и  на координатные оси прямоугольной системы координат дается формулой

     (27)

которую можно записать с помощью определителя

     (28)

Проекции векторного произведения на оси прямоугольной системы координат вычисляются по формулам

     (29)

и тогда на основании (4)

     (30)

Механический смысл векторного произведения состоит в следующем: если вектор  - сила, а вектор  есть радиус-вектор точки приложения силы, имеющий свое начало в точке O, то момент силы  относительно точки O  есть вектор, равный векторному произведению радиуса-вектора  точки приложения силы на силу , т. е.

19. Векторно-скалярное произведение трех векторов ,  и  или смешанное их произведение вычисляется по формуле

     (31)

Абсолютная величина векторно-скалярного произведения равна объему параллелепипеда, построенного на векторах ,  и . Объем пирамиды, построенной на векторах ,  и , получим по формуле

     (32)

причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы ,  и  не лежат в одной плоскости).

20. Три вектора ,  и  называются компланарными, если они лежат в одной плоскости или параллельны одной и той же плоскости. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение было равно нулю.

Ба́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

Линейные комбинации

Конечная сумма вида

называется^[3] линейной комбинацией элементов  с коэффициентами .

В действительности данное определение (и приводимые ниже) приложимо не только к комбинациям векторов, но и к комбинациям любых других объектов, для которых подобные суммы вообще имеют смысл (например, к комбинациям точек аффинного пространства).

Линейная комбинация называется нетривиальной, если хотя бы один из её коэффициентов отличен от нуля.

Линейная комбинация называется^[4] барицентрической, если сумма её коэффициентов равна 1, и сбалансированной, если эта сумма равна 0.

Линейная зависимость векторов

Введем еще одно очень важное понятие, которое используется не только в алгебре, но и во многих других разделах математики.

        Определение 10.14   Система векторов  называется линейно зависимой, если существует такой набор коэффициентов  , из которых хотя бы один отличен от нуля, что  .         

Система векторов, которая не является линейно зависимой, называется линейно независимой. Но последнее определение лучше сформулировать по другому.

        Определение 10.15   Система векторов  называется линейно независимой, если равенство  возможно только при  .         

Кто плохо понял два последних определения, может получить дополнительные объяснения здесь.

        Предложение 10.6   Система векторов  линейно зависима тогда и только тогда, когда один из векторов системы является линейной комбинацией остальных векторов этой системы.

        Доказательство.     Пусть система векторов линейно зависима. Тогда существует такой набор коэффициентов  , что  , причем хотя бы один коэффициент отличен от нуля. Предположим, что  . Тогда

то есть  является линейной комбинацией остальных векторов системы.

Пусть один из векторов системы является линейной комбинацией остальных векторов. Предположим, что это вектор  , то есть  . Очевидно, что  . Получили, что линейная комбинация векторов системы равна нулю, причем один из коэффициентов отличен от нуля (равен  ).      

        Предложение 10.7   Если система векторов содержит линейно зависимую подсистему, то вся система линейно зависима.

        Доказательство.    

Пусть в системе векторов  подсистема  ,  , является линейно зависимой, то есть  , и хотя бы один коэффициент отличен от нуля. Тогда составим линейную комбинацию  . Очевидно, что эта линейная комбинация равна нулю, и что среди коэффициентов есть ненулевой.      

№8

Декартова система координат

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

№9