Матрицы

1. Матрицы и их типы

Матрица – это совокупность чисел или объектов другой природы, расположенных в виде прямоугольной таблицы.

.

mстрок nстолбцов

Размер матрицы .

.

Мы будем рассматривать конечные матрицы с числовыми элементами.

Классификация по размеру

1) – матрица-столбец.

2) – матрица-строка.

3) , т.е.– квадратная матрица.

Элементы , где– образуют главную диагональ.

4) Квадратная матрица, все элементы которой вне главной диагонали равны нулю, называется диагональной.

.

5) Если в диагональной матрице все , то такая матрица называетсяединичной.

.

Единичную матрицу удобно обозначать с помощью символа Кронекера

.

6) Нулеваяматрица

.

У нее все элементы равны нулю.

Транспонированиематрицы – это преобразование, состоящее в замене строк столбцами. Получим транспонированную матрицу.

Например.

.

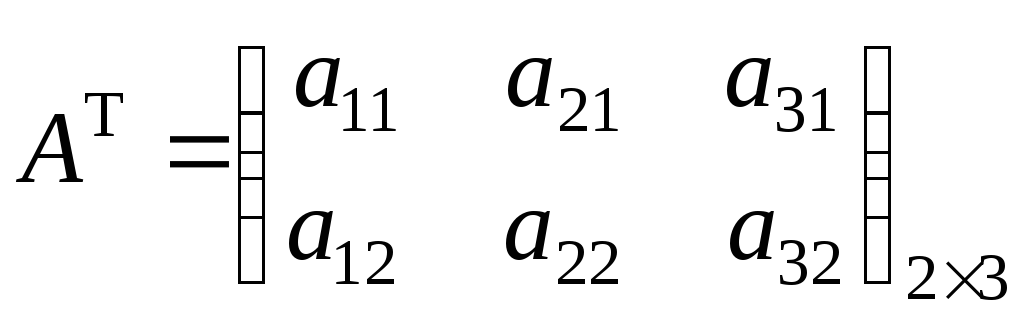Очевидно свойство

.

Если , то матрица называетсясимметричной. И у нее

,

т.е. равны элементы, симметричные относительно главной диагонали.

Если , то матрица называетсякососимметричной. У нее

.

Очевидно, что у такой матрицы элементы главной диагонали равны нулю.

Для равенстваматриц необходимо и достаточно, чтобы они были одинакового размера и чтобы элементы, стоящие на одинаковых местах были равными.

2. Операции над матрицами

1. Сумма матриц.

Матрицы одинаковых размеров можно складывать, при этом получаем матрицу того же размера, что и слагаемые, а элементы ее образуются сложением элементов, стоящих на одинаковых местах

.

Пример.

.

Эта операция обладает свойствами:

1. Коммутативность

.

2. Ассоциативность

.

3. .

4. ,;

,.

2. Произведение матрицы на число.

Любую матрицу можно умножить на число (скаляр), при этом получаем матрицу того же размера, а элементы ее получаются умножением на заданное число всех элементов данной матрицы.

.

Пример.

.

Свойства этой операции:

1. Дистрибутивность относительно матричной суммы

.

2. Дистрибутивность относительно скалярной суммы

.

3. Ассоциативность относительно произведения скаляров

.

4. Существование элемента нейтрального относительно умножения на скаляр

.

3. Умножение матриц.

а) Умножение строки на столбец.

Это возможно, если число элементов в строке равно числу элементов в столбце.

.

Пример.

.

б) Умножение произвольных матриц.

Произведением матрицы на матрицуявляется матрицаразмера, элементкоторой равен результату умноженияi^ойстроки матрицыАнаk^ыйстолбец матрицыВ

.

Пример.

.

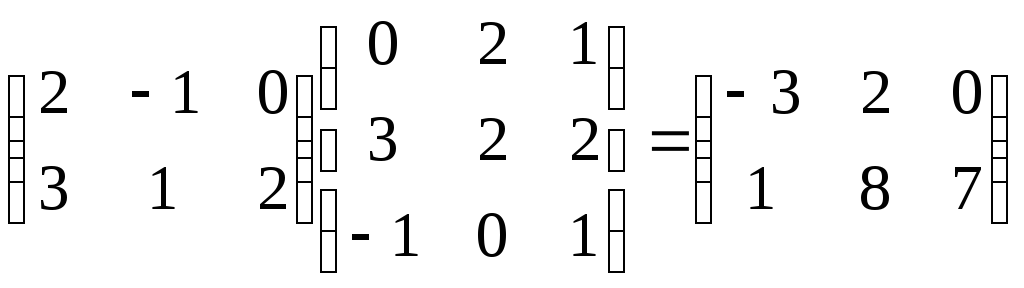Ясно, что умножать матрицы можно не всегда, а с точки зрения их размеров.

Правило размеров:

.

Поэтому в общем случае произведение матриц не коммутативно.

.

Если же , то такие матрицы называютсякоммутирующими. Однако, если операция произведения осуществима, то будут справедливы следующие свойства:

1. Ассоциативность

.

2. Дистрибутивность.

или

.

Рассмотрим выполнение заданий на действие с матрицами.

Задание 1

Найти матрицу C= 3A+ 4B, если

.

Решение

Используя свойства сложения и умножения матриц на число, получим

Задание 2

Показать, что матрица S= 3A– 2B – симметрическая, если

.

Решение

Используя свойства сложения и умножения матриц на число, получим

Полученная матрица S– симметрическая, так как при транспонировании она не изменяется.

Задание 3

Показать, что матрица K= 5A–B – кососимметрическая, если

.

Решение

Используя свойства сложения и умножения матриц на число, получим

Полученная матрица K– кососимметрическая, так как при транспонировании она меняет знак на противоположный:

Задание 4

Найти матрицу C=AB, если

.

Решение

Данные матрицы удовлетворяют правилу размеров (4), а следовательно, их можно перемножить. Найдем элементы первой строки матрицы С, используя формулу (3) и схему:

===

===

===

Аналогично находим все остальные элементы матрицы С:

Следовательно, матрица Симеет вид:

Задание 5

Найти матрицу C=AB, если

.

Решение

Данные матрицы удовлетворяют правилу размеров (4), а следовательно, их можно перемножить. Умножая по очереди строки матрицы Ана столбцы матрицыВ, получим матрицу

Задание 6

Показать, что произведение матрицы на транспонированную является симметрической матрицей.

Решение

Транспонируем матрицу A:

.

Матрицы AиA^Tудовлетворяют правилу размеров (4), а следовательно, их можно перемножить. Умножая по очереди строки матрицыАна столбцы матрицыA^T, получим матрицу

Матрица S является симметрической, так как при транспонировании она не меняется, т.е.S = S^Т, что и требовалось доказать.

Задание 7

Показать, что матрицы A и B перестановочны.

.

Решение

Данные матрицы удовлетворяют правилу размеров (4), а, следовательно, их можно перемножить в любом порядке.

Найдем произведение АВ. Умножая по очереди строки матрицыАна столбцы матрицыВ, получим матрицу

Теперь перемножим эти же матрицы в другом порядке, т.е. найдем произведение ВА:

Так как АВ=ВА, то исходные матрицы перестановочны, что и требовлось показать.

Задание 8

Выполнить действия:

.

Решение

Данные матрицы удовлетворяют правилу размеров (4), а следовательно, их можно перемножить и затем сложить:

Следующее задание выполните самостоятельно:

Задание 9

Выполнить действия

.

Если у Вас получился результат отличный от матрицы

, то рассмотрите решение этого задания.

Решение задания 9.

Данные матрицы удовлетворяют правилу размеров (4), а, следовательно, их можно перемножить и затем сложить:

3. Ранг матрицы

Для квадратной матрицы Аможно записать определитель, состоящий из тех же элементов. Обозначается

detA.

Если , то матрица называетсянеособенной(вырожденной). Если–вырожденная (особенная).

Пусть дана прямоугольная матрица размера . Образуем минорk^гопорядка этой матрицы. Для этого возьмемkстрок иkстолбцов и выберем элементы, стоящие на их пересечениях. Из этих элементов составим определитель. Порядок его будетk. Это и есть минорk^гопорядка матрицыА.

Например.

;;

.

Ясно, что таких миноров можно образовать несколько.

Будем образовывать такие миноры, начиная с порядка , затеми т.д. При некотором порядкехотя бы один из миноров этого порядка не равен нулю, а при, т.е. повышении порядка на единицу, уже все миноры будут равны нулю.

Такое число rи называется рангом матрицыА.

или

.

Минор порядка r, который отличен от нуля, называетсябазисным минором, а строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками или столбцами.

Естественно, что таких базисных миноров может быть несколько.

Пример.

. Найти ранг этой матрицы.

Решение. Среди всех миноров 1^гопорядка (отдельные элементы) есть ненулевые. Значит ранг не меньше 1.

Среди всех миноров 2^гопорядка есть ненулевые. Например.

Значит ранг не меньше 2.

Переберем все миноры третьего порядка.

;;;.

Все миноры третьего порядка нулевые.

Ранг равен 2.

Для вычисления ранга матрицы очень часто пользуются приемом проведения ее к виду, позволяющему дать ответ о ранге исследуемой матрицы. Для этого применяют операции, не изменяющие ранг матрицы, но упрощающие ее вид.

Эти операции называются элементарными, и они вытекают из свойств определителей:

1. Транспонирование матрицы.

2. Перестановка строк (столбцов).

3. Умножение всех элементов строки (столбца) на какое-либо число.

4. Прибавление к одному столбцу (строке) другого, умноженного на отличное от нуля число.

Пример. Найти ранг матрицы.

~~

~~

.

Каноническойназывается матрица, у которой в начале главной диагонали стоят несколько единиц, а все остальные равны нулю.

Например

.

Очевидно .

При помощи элементарных преобразований любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Рассмотрим выполнение заданий на нахождение ранга матрицы.

Задание 1

Вычислить ранг матрицы .

Решение

Все элементы данной матрицы, т.е. миноры первого порядка, отличны от нуля. Следовательно, ранг матрицы Ане меньше 1.

Вычислим определитель данной матрицы (единственный минор второго порядка):

Так как определитель матрицы А, т.е. ее минор второго порядка, отличен от нуля, то ранг данной матрицыr(A) = 2. Определитель матрицыАбудет ее единственным базисным минором.

Ответ: r(A) = 2.

Задание 2

Вычислить ранг матрицы .

Решение

Все элементы матрицы А, т.е. миноры первого порядка, отличны от нуля. Следовательно, ранг матрицыАне меньше 1. Однако определитель ее, т.е. ее минор второго порядка, равен нулю:

Следовательно, ранг данной матрицы r(A) = 1. Данная матрица имеет четыре базисных минора :

Ответ: r(A) = 1.

Задание 3

Вычислить ранг матрицы .

Решение

Один элемент матрицы А, т.е. один минор первого порядка, отличен от нуля. Следовательно, ранг матрицыАне меньше 1. Однако определитель ее, т.е. ее минор второго порядка, равен нулю:

Следовательно, ранг данной матрицы r(A) = 1. Данная матрица имеет один базисный минор

Ответ: r(A) = 1.

Задание 4

Вычислить ранг матрицы.

Решение

Так как все элементы матрицы А, т.е. миноры первого порядка, равны нулю, то ранг данной матрицыr(A) = 0.

Ответ: r(A) = 0.

Задание 5

Вычислить ранг матрицы .

Решение

Все элементы данной матрицы, т.е. миноры первого порядка, отличны от нуля. Следовательно, ранг матрицы Ане меньше 1.

Среди миноров второго порядка есть ненулевые. Например, .

Значит, ранг не меньше 2.

Вычислим определитель данной матрицы (единственный минор третьего порядка):

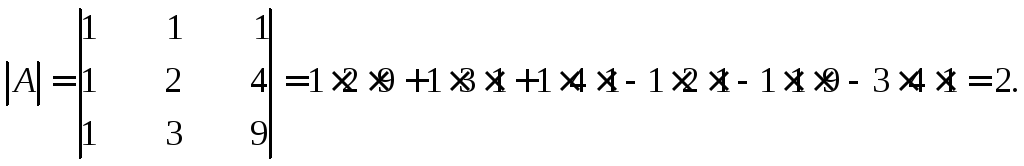
Так как определитель матрицы А, т.е. ее минор третьего порядка, отличен от нуля, то ранг данной матрицыr(A) = 3. Определитель данной матрицыАбудет так же ее единственным базисным минором.

Ответ: r(A) = 3.

Задание 6

Вычислить ранг матрицы .

Решение

Все элементы данной матрицы, т.е. миноры первого порядка, отличны от нуля. Следовательно, ранг матрицы Ане меньше 1.

Среди миноров второго порядка есть ненулевые. Например, .

Значит, ранг не меньше 2.

Вычислим определитель данной матрицы (единственный минор третьего порядка):

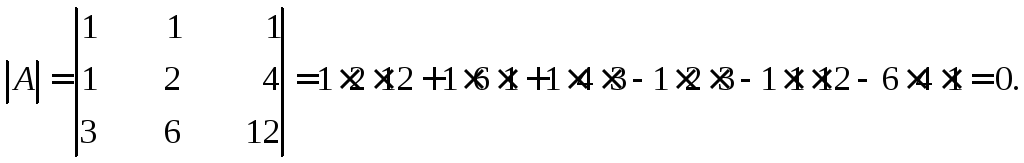
Определитель матрицы А, ее минор третьего порядка, равен нулю. Значит ранг данной матрицыr(A) = 2. Данная матрица имеет шесть базовых миноров:

Ответ: r(A) = 2.

Задание 7

Найти ранг матрицы .

Решение

Посредством последовательных элементарных преобразований над данной матрицей получим следующую систему эквивалентных матриц:

~~~

~ ~~~.

Следовательно, ранг данной матрицы равен двум.

Ответ:r(A)= 2.

Задание 8

Найти ранг матрицы .

Решение

Посредством последовательных элементарных преобразований над данной матрицей получим следующую систему эквивалентных матриц:

~~~

~ ~~.

Следовательно, ранг данной матрицы равен двум.

Ответ:r(A)= 2.

Задание 9

Найти ранг матрицы .

Решение

Посредством последовательных элементарных преобразований над данной матрицей получим следующую систему эквивалентных матриц:

~~

~~~

~ ~~

~ ~~

~ ~.

Следовательно, ранг данной матрицы равен двум.

Ответ:r(A)= 2.

Следующее задание выполните самостоятельно

Задание 10

Найти ранг матрицы .Если у Вас получился иной результат чем r(A)= 3, то рассмотрите решение задания 10.

Решение задания 10.

Посредством последовательных элементарных преобразований над данной матрицей получим следующую систему эквивалентных матриц:

~~

~ ~~

~ ~~

~ ~.

Следовательно, ранг данной матрицы равен трем.

Ответ:r(A)= 3.

4. Матричная запись систем линейных уравнений. Обратная матрица

Первоначально матрицы были введены для упрощения записи систем линейных уравнений. Это и обусловило определение основных матричных операций.

Пусть дана система тлинейных уравнений сnнеизвестными.

(1)

В матричной форме:

(2)

|| || ||

А ∙ Х = В

А– матрица системы;

Х– матрица неизвестных;

В– матрица свободных членов.

Получим сокращенную запись системы:

(3)

Будем рассматривать систему n-линейных уравнений сnнеизвестными. В этом случаеА– квадратная матрица размера. Если эта матрица невырожденная, то ее ранг равенn.

Введем понятие обратной матрицы.

В алгебре два числа, произведение которых равно 1, называются взаимно обратными.

.

Имеет место некоторая аналогия и для матричной алгебры.

Определение.

Две квадратные матрицы, произведение которых равно единичной матрице, называются взаимно обратными.

Обозначение .

По определению

.

Теперь, используя обратную матрицу, решим матричное уравнение (3). Для этого умножим обе части (3) на .

;

;

. (4)

Это и есть матричное решение системы уравнений.

Значит решение системы сводится к отысканию обратной матрицы и ее умножению на матрицу свободных членов.

Теорема(существования и единственности обратной матрицы).

Если А– квадратная невырожденная матрица, т.е., то для нее существует единственная обратная матрица.

Доказательство.

Будем рассматривать для простоты матрицу .

.

1. Запишем для Атранспонированную матрицу

.

2. Запишем в каждый элемент дополнением. Получим так называемую союзную (присоединенную) матрицу.

.

3. Вычислим произведение .

∆

∆

∆

0

0

0

0

0

0

где .

Аналогично проверим и другое произведение

.

Итак, имеем

,

откуда, т.к. ,

.

Сравнивая это равенство с определением обратной матрицы, можем сказать, что

.

Мы доказали существование обратной матрицы при условии, что . Покажем ее единственность.

От противного:

Предположим, что существуют две различные обратные матрицы для матрицы А. Этои.

Тогда

.

Умножаем обе части на

.

Применяя сочетательное свойство, получим

,

откуда

.

Что противоречит предположению о том, что имеются две различные обратные матрицы.

Из доказанной теоремы следует алгоритм построения обратной матрицы:

1. Вычисляем . Если, то.

2. Транспонируем .

3. Строим заменой.

4. .

Пример. Найти для.

Решение: 1) .

2) .

3) .

4) .

Проверка.

.

Обратная матрица обладает свойствами:

1с) .

Доказательство:

.

2с) .

3с) .

4с) .

Эти свойства доказываются аналогично свойству 1с) и путем вычисления.

Существует и другой способ вычисления обратной матрицы, основанный на элементарных преобразованиях вспомогательной матрицы, которая получается путем приписывания к данной матрице единичной матрицы того же размера.

.

Пример.

.

5. Теорема Кронекера-Капелли

Рассмотрим систему mлинейных уравнений сnнеизвестными:

Матрица системы:

.

Расширенная матрица системы:

.

Очевидно .

Теорема Кронекера-Капелли утверждает, что

1)система имеет единственное решение (определенна).

2)система имеет бесконечное множество решений (неопределенна)

3)система не имеет решений (несовместна)

Примеры.

1)

~.

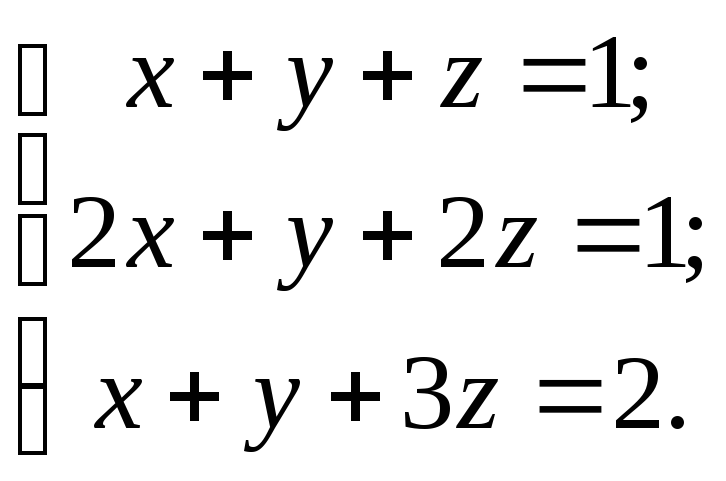
А

определенна.

Решение ,,.

2)

.

,.

.

3)

.

,.

бесконечное множество решений.

.

,,.

Рассмотрим выполнение заданий на нахождение обратной матрицы и решение систем линейных уравнений с помощью обратной матрицы.

Задание1

Найти матрицу, обратную матрице .

Решение