
Тема 12 Корреляционный анализ
Функциональная зависимость и корреляция. Еще Гиппократ в VI в. до н. э. обратил внимание на наличие связи между телосложением и темпераментом людей, между строением тела и предрасположенностью к тем или иным заболеваниям. Определенные виды подобной связи выявлены также в животном и растительном мире. Так, существует зависимость между телосложением и продуктивностью у сельскохозяйственных животных; известна связь между качеством семян и урожайностью культурных растений и т.д. Что же касается подобных зависимостей в экологии, то существуют зависимости между содержанием тяжелых металлов в почве и снежном покрове от их концентрации в атмосферном воздухе и т.п. Поэтому естественно стремление использовать эту закономерность в интересах человека, придать ей более или менее точное количественное выражение.
Как
известно, для описания связей между
переменными величинами применяют
математические понятие функции f,
которая ставит в соответствие каждому
определенному значению независимой
переменной x
определенное значение зависимой
переменной y,
т.е.
 .
Такого рода однозначные зависимости
между переменными величинамиx
и
y
называют
функциональными.
Однако такого рода связи в природных
объектах встречаются далеко не всегда.
Поэтому зависимость между биологическими,
а также и экологическими признаками
имеет не функциональный, а статистический
характер, когда в массе однородных
индивидов определенному значению одного
признака, рассматриваемого в качестве
аргумента, соответствует не одно и то
же числовое значение, а целая гамма
распределяющихся в вариационный ряд
числовых значений другого признака,
рассматриваемого в качестве зависимой
переменной, или функции. Такого рода
зависимость между переменными величинами
называется корреляционной
или корреляцией..
.
Такого рода однозначные зависимости
между переменными величинамиx
и
y
называют
функциональными.
Однако такого рода связи в природных
объектах встречаются далеко не всегда.
Поэтому зависимость между биологическими,
а также и экологическими признаками
имеет не функциональный, а статистический
характер, когда в массе однородных
индивидов определенному значению одного
признака, рассматриваемого в качестве
аргумента, соответствует не одно и то
же числовое значение, а целая гамма
распределяющихся в вариационный ряд
числовых значений другого признака,
рассматриваемого в качестве зависимой
переменной, или функции. Такого рода
зависимость между переменными величинами
называется корреляционной
или корреляцией..
Функциональные связи легко обнаружить и измерить на единичных и групповых объектах, однако этого нельзя проделать с корреляционными связями, которые можно изучать только на групповых объектах методами математической статистики. Корреляционная связь между признаками бывает линейной и нелинейной, положительной и отрицательной. Задача корреляционного анализа сводится к установлению направления и формы связи между варьирующими признаками, измерению ее тесноты и, наконец, к проверке достоверности выборочных показателей корреляции.
Зависимость
между переменными X
и Y
можно выразить аналитически (с помощью
формул и уравнений) и графически (как
геометрическое место точек в системе
прямоугольных координат). График
корреляционной зависимости строят по
уравнению функции
 или
или ,
которая называетсярегрессией.
Здесь
,
которая называетсярегрессией.
Здесь
 и
и – средние арифметические, найденные
при условии, чтоX
или Y
примут некоторые значения x
или y.
Эти средние называются условными.
– средние арифметические, найденные
при условии, чтоX
или Y
примут некоторые значения x
или y.
Эти средние называются условными.
11.1. Параметрические показатели связи
Коэффициент корреляции. Сопряженность между переменными величинами x и y можно установить, сопоставляя числовые значения одной из них с соответствующими значениями другой. Если при увеличении одной переменной увеличивается другая, это указывает на положительную связь между этими величинами, и наоборот, когда увеличение одной переменной сопровождается уменьшением значения другой, это указывает на отрицательную связь.
Для характеристики связи, ее направления и степени сопряженности переменных применяют следующие показатели:
линейной зависимость – коэффициент корреляции;
нелинейный – корреляционной отношение.
Для определения эмпирического коэффициента корреляции используют следующую формулу:
 .
(1)
.
(1)
Здесь sx и sy – средние квадратические отклонения.
Коэффициент корреляции можно вычислить, не прибегая к расчету средних квадратических отклонений, что упрощает вычислительную работу, по следующей аналогичной формуле:
 . (2)
. (2)
Коэффициент
корреляции – безразмерное число, лежащее
в пределах от –1 до +1. При независимом
варьировании признаков, когда связь
между ними полностью отсутствует,
 .
Чем сильнее сопряженность между
признаками, тем выше значение коэффициента
корреляции. Следовательно, при
.
Чем сильнее сопряженность между
признаками, тем выше значение коэффициента
корреляции. Следовательно, при этот показатель характеризует не только
наличие, но и степень сопряженности
между признаками. При положительной
или прямой связи, когда большим значениям
одного признака соответствуют большие
же значения другого, коэффициент
корреляции имеет положительный знак и
находится в пределах от 0 до +1, при
отрицательной или обратной связи, когда
большим значениям одного признака
соответствуют меньшие значения другого,
коэффициент корреляции сопровождается
отрицательным знаком и находится в
пределах от 0 до –1.
этот показатель характеризует не только
наличие, но и степень сопряженности
между признаками. При положительной
или прямой связи, когда большим значениям
одного признака соответствуют большие
же значения другого, коэффициент
корреляции имеет положительный знак и
находится в пределах от 0 до +1, при
отрицательной или обратной связи, когда
большим значениям одного признака
соответствуют меньшие значения другого,
коэффициент корреляции сопровождается
отрицательным знаком и находится в
пределах от 0 до –1.
Коэффициент корреляции нашел широкое применение в практике, но он не является универсальным показателем корреляционных связей, так как способен характеризовать только линейные связи, т.е. выражаемые уравнением линейной регрессии (см. тему 12). При наличии нелинейной зависимости между варьирующими признаками применяют другие показатели связи, рассмотренных ниже.
Вычисление коэффициента корреляции. Это вычисление производят разными способами и по-разному в зависимости от числа наблюдений (объема выборки). Рассмотрим отдельно специфику вычисления коэффициента корреляции при наличии малочисленных выборок и выборок большого объема.
Малые
выборки.
При наличии малочисленных выборок
коэффициент корреляции вычисляют
непосредственно по значениям сопряженных
признаков, без предварительной группировки
выборочных данных в вариационные ряды.
Для этого служат приведенные выше
формулы (1) и (2). Более удобными, особенно
при наличии многозначных и дробных
чисел, которыми выражаются отклонения
вариант хi
и yi
от средних
 и
и ,
служат следующие рабочие формулы:
,
служат следующие рабочие формулы:
 ,
(3)
,
(3)
где
 ;
;
 ;
;
 .
.
Здесь
xi
и yi
– парные варианты сопряженных признаков
x
и
y;
 и
и
 –средние арифметические;
–средние арифметические; – разность между парными вариантами
сопряженных признаковx
и
y;
n
– общее число парных наблюдений, или
объем выборочной совокупности.
– разность между парными вариантами
сопряженных признаковx
и
y;
n
– общее число парных наблюдений, или
объем выборочной совокупности.
Эмпирический коэффициент корреляции, как и любой другой выборочный показатель, служит оценкой своего генерального параметра ρ и как величина случайная сопровождается ошибкой:
 . (4)
. (4)
Отношение
выборочного коэффициента корреляции
к своей ошибке служит критерием для
проверки нулевой гипотезы – предположения
о том, что в генеральной совокупности
этот параметр равен нулю, т.е.
 .
Нулевую гипотезу отвергают на принятом
уровне значимостиα,
если
.
Нулевую гипотезу отвергают на принятом
уровне значимостиα,
если
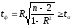 . (5)
. (5)
Значения
критических точек tst
для
разных уровней значимости α
и
чисел степеней свободы
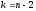 приведены в табл.1 Приложений.
приведены в табл.1 Приложений.
Установлено, что при обработке малочисленных выборок (особенно когда n < 30) расчет коэффициента корреляции по формулам (1) – (3) дает несколько заниженные оценки генерального параметра ρ, т.е. необходимо внести следующую поправку:
 . (6)
. (6)
z-преобразование Фишера. Правильное применение коэффициента корреляции предполагает нормальное распределение двумерной совокупности сопряженных значений случайных величин x и y. Из математической статистики известно, что при наличии значительной корреляции между переменными величинами, т.е. когда Rxy > 0,5 выборочное распределение коэффициента корреляции для большего числа малых выборок, взятых из нормально распределяющейся генеральной совокупности, значительно отклоняются от нормальной кривой.
Учитывая это обстоятельство, Р. Фишер нашел более точный способ оценки генерального параметра по значению выборочного коэффициента корреляции. Этот способ сводится к замене Rxy преобразованной величиной z, которая связана с эмпирическим коэффициентом корреляции, следующим образом:
 . (7)
. (7)
Распределение величины z является почти неизменным по форме, так как мало зависит от объема выборки и от значения коэффициента корреляции в генеральной совокупности, и приближается к нормальному распределению.
Критерием достоверности показателя z является следующее отношение:
 . (7)
. (7)
Нулевая
гипотеза отвергается на принятом уровне
значимости α
и числе степеней свободы
 .
Значения критических точекtst
приведены
в табл.1 Приложений.
.
Значения критических точекtst
приведены
в табл.1 Приложений.
Применение
z-преобразования
позволяет с большей уверенностью
оценивать статистическую значимость
выборочного коэффициента корреляции,
а также и разность между эмпирическими
коэффициентами
 ,
когда в этом возникает необходимость.
,
когда в этом возникает необходимость.
Минимальный объем выборки для точной оценки коэффициента корреляции. Можно рассчитать объем выборки для заданного значения коэффициента корреляции, который был бы достаточен для опровержения нулевой гипотезы (если корреляция между признаками Y и X действительно существует). Для этого служит следующая формула:
 ,
(8)
,
(8)
где n – искомый объем выборки; t – величина, заданная по принятому уровню значимости (лучше для α = 1%); z – преобразованный эмпирический коэффициент корреляции.
Большие выборки. При наличии многочисленных исходных данных их приходится группировать в вариационные ряды и, построив корреляционную решетку, разность по ее клеткам (ячейкам) общие частоты сопряженных рядов. Корреляционная решетка образуется пересечением строк и столбцов, число которых равно числу групп или классов коррелируемых рядов. Классы располагаются в верхней строке и в первой (слева) столбце корреляционной таблицы, а общие частоты, обозначаемые символом fxy, – в клетках корреляционной решетки, составляющей основную часть корреляционной таблицы.
Классы, помещенные в верхней строке таблицы, обычно располагаются слева направо в возрастающем порядке, а в первом столбце таблицы – сверху вниз в убывающем порядке. При таком расположении классов вариационных рядов их общие частоты (при наличии положительной связи между признаками Y и X) будут распределяться по клеткам решетки в виде эллипса по диагонали от нижнего левого угла к верхнему правому углу решетки или (при наличии отрицательной связи между признаками) в направлении от верхнего левого угла к нижнему правому углу решетки. Если же частоты fxy распределяются по клеткам корреляционной решетки более или менее равномерно, не образуя фигуры эллипса, это будет указывать на отсутствие корреляции между признаками.
Распределение частот fxy по клеткам корреляционной решетки дает лишь общее представление о наличии или отсутствии связи между признаками. Судить о тесноте или менее точно лишь по значению и знаку коэффициента корреляции. При вычислении коэффициента корреляции с предварительной группировки выборочных данных в интервальные вариационные ряды не следует брать слишком широкие классовые интервалы. Грубая группировка гораздо сильнее сказывается на значении коэффициента корреляции, чем это имеет место при вычислении средних величин и показателей вариации.
Напомним, что величина классового интервала определяется по формуле
 ,
(9)
,
(9)
где xmax, xmin – максимальная и минимальная варианты совокупности; К – число классов, на которые следует разбить вариацию признака. Опыт показал, что в области корреляционного анализа величину К можно поставить в зависимость от объема выборки примерно следующим образом (табл.1).
Таблица 1
|
Объем выборки |
Значение К |
|
50 ≥ n > 30 |
|
|
100 ≥ n > 50 |
|
|
200 ≥ n > 100 |
|
|
300 ≥ n > 200 |
|
Как и другие статистические характеристики, вычисляемые с предварительной группировкой исходных данных в вариационные ряды, коэффициент корреляции определяют разными способами, дающими совершенно идентичные результаты.
Способ
произведений.
Коэффициент корреляции можно вычислить
используя основные формулы (1) или (2),
внеся в них поправку на повторяемость
вариант в димерной совокупности. При
этом, упрощая символику, отклонения
вариант от их средних обозначим через
а,
т.е.
 и
и .
Тогда формула (2) с учетом повторяемости
отклонений примет следующее выражение:
.
Тогда формула (2) с учетом повторяемости
отклонений примет следующее выражение:
 .
(10)
.
(10)
Достоверность этого показателя оценивается с помощью критерия Стьюдента, который представляет отношение выборочного коэффициента корреляции к своей ошибке, определяемой по формуле
 . (11)
. (11)
Отсюда
 и если эта величина превышает стандартное
значение критерия Стьюдентаtst
для степени свободы
и если эта величина превышает стандартное
значение критерия Стьюдентаtst
для степени свободы
 и уровне значимостиα
(см.
Таблицу 2 Приложений), то нулевую гипотезу
отвергают.
и уровне значимостиα
(см.
Таблицу 2 Приложений), то нулевую гипотезу
отвергают.
Способ
условных средних.
При вычислении коэффициента корреляции
отклонения вариант (“классов”)
можно находить не только от средних
арифметических
 и
и ,
но и от условных средних Ах
и Ay.
При этом способе в числитель формулы
(2) вносят поправку и формула приобретает
следующий вид:
,
но и от условных средних Ах
и Ay.
При этом способе в числитель формулы
(2) вносят поправку и формула приобретает
следующий вид:
 , (12)
, (12)
где
fxy
– частоты классов одного и другого
рядов распределения;
 и
и ,
т.е. отклонения классов от условных
средних, отнесенные к величине классовых
интерваловλ;
n
– общее число парных наблюдений, или
объем выборки;
,
т.е. отклонения классов от условных
средних, отнесенные к величине классовых
интерваловλ;
n
– общее число парных наблюдений, или
объем выборки;
 и
и – условные моменты первого порядка,
гдеfx
– частоты ряда Х,
а
fy
– частоты ряда Y;
sx
и
sy
– средние квадратические отклонения
рядов X
и
Y,
вычисляемые по формуле
– условные моменты первого порядка,
гдеfx
– частоты ряда Х,
а
fy
– частоты ряда Y;
sx
и
sy
– средние квадратические отклонения
рядов X
и
Y,
вычисляемые по формуле
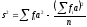 .
.
Способ условных средних имеет преимущество перед способом произведений, так как позволяет избегать операции с дробными числами и придавать один и тот же (положительный) знак отклонениям ax и ay, что упрощает технику вычислительной работы, особенно при наличии многозначных чисел.
Оценка разности между коэффициентами корреляции. При сравнении коэффициентов корреляции двух независимых выборок нулевая гипотеза сводится к предположению о том, что в генеральной совокупности разница между этими показателями равна нулю. Иными словами, следует исходить из предположения, что разница, наблюдаемая между сравниваемыми эмпирическими коэффициентами корреляции, возникла случайно.
Для проверки нулевой гипотезы служит t-критерий Стьюдента, т.е. отношение разности между эмпирическими коэффициентами корреляции R1 и R2 к своей статистической ошибке, определяемой по формуле:
 , (13)
, (13)
где sR1 и sR2 – ошибки сравниваемых коэффициентов корреляции.
Нулевая
гипотеза опровергается при условии,
что
 для принятого уровне значимостиα
и числе степеней свободы
для принятого уровне значимостиα
и числе степеней свободы
 .
.
Известно, что более точную оценку достоверности коэффициента корреляции получают при переводе Rxy в число z. Не является исключением и оценка разности между выборочными коэффициентами корреляции R1 и R2, особенно в тех случаях, когда последние вычислены на выборках сравнительно небольшого объема (n < 100) и по своему абсолютному значению значительно превышают 0,50.
Разность
 оценивают с помощью t-критерия Стьюдента,
который строят по отношению этой разности
к своей ошибке, вычисляемой по формуле
оценивают с помощью t-критерия Стьюдента,
который строят по отношению этой разности
к своей ошибке, вычисляемой по формуле
 . (14)
. (14)
Нулевую
гипотезу отвергают, если
 для
для и принятого уровня значимостиα.
и принятого уровня значимостиα.
Корреляционное
отношение.
Для измерения нелинейной зависимости
между переменными x
и
y
используют показатель, который называют
корреляционным
отношением,
который описывает связь двусторонне.
Конструкция корреляционного отношения
предполагает сопоставление двух видов
вариации: изменчивости отдельных
наблюдений по отношению к частным
средним и вариации самих частных средних
по сравнению с общей средней величиной.
Чем меньшую часть составит первый
компонент по отношению ко второму, тем
теснота связи окажется большей. В
пределе, когда никакой вариации отдельных
значений признака возле частных средних
не будет наблюдаться, теснота связи
окажется предельно большой. Аналогичным
образом, при отсутствии изменчивости
частных средних теснота связи окажется
минимальной. Так как это соотношение
вариации может быть рассмотрено для
каждого из двух признаков, получается
два показателя тесноты связи – hyx
и hxy.
Корреляционное отношение является
величиной относительной и может принимать
значения от 0 до 1. При этом коэффициенты
корреляционного отношения обычно не
равны друг другу, т.е.
 .
Равенство между этими показателями
осуществимо только при строго линейной
зависимости между признаками.
Корреляционное отношение является
универсальным показателем: оно позволяет
характеризировать любую форму
корреляционной связи – и линейную, и
нелинейную.
.
Равенство между этими показателями
осуществимо только при строго линейной
зависимости между признаками.
Корреляционное отношение является
универсальным показателем: оно позволяет
характеризировать любую форму
корреляционной связи – и линейную, и
нелинейную.
Коэффициенты корреляционного отношения hyx и hxy определяют рассмотренными выше способами, т.е. способом произведений и способом условных средних.
Способ произведений. Коэффициенты корреляционного отношения hyx и hxy определяют по следующим формулам:
 и
и
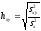 , (15)
, (15)
где
 и
и – групповые дисперсии,
– групповые дисперсии,
а
 и
и – общие дисперсии.
– общие дисперсии.
Здесь
 и
и – общие средние арифметические, а
– общие средние арифметические, а и
и – групповые средние арифметические;fyi
– частоты ряда Y,
а fxi
–
частоты ряда X;
k
– количество классов; n
– количество варьирующих признаков.
– групповые средние арифметические;fyi
– частоты ряда Y,
а fxi
–
частоты ряда X;
k
– количество классов; n
– количество варьирующих признаков.
Рабочие формулы для расчета коэффициентов корреляционного отношения следующие:
 и
и
 . (16)
. (16)
Способ
условных средних.
Определяя коэффициенты корреляционного
отношения по формулам (15), отклонения
классовых вариант xi
и yi
можно брать не только от средних
арифметических
 и
и ,
но и от условных средних Ах
и Ay.
В таких случаях групповые и общие девиаты
рассчитываются по формулам
,
но и от условных средних Ах
и Ay.
В таких случаях групповые и общие девиаты
рассчитываются по формулам
 и
и ,
а также,
,
а также, и
и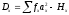 ,
где
,
где и
и .
.
В развернутом виде формулы (15) выглядят следующим образом:
 ;
;
 . (17)
. (17)
В
этих формулах
 и
и – отклонения классов от условных
средних, сокращенные на величину
классовых интервалов; значенияay
и ax
выражаются
числами натурального ряда: 0, 1, 2, 3, 4, …
.Остальные символы объяснены выше.
– отклонения классов от условных
средних, сокращенные на величину
классовых интервалов; значенияay
и ax
выражаются
числами натурального ряда: 0, 1, 2, 3, 4, …
.Остальные символы объяснены выше.
Сравнивая способ произведений со способом условных средних, нельзя не заметить преимущество первого способа, особенно в тех случаях, когда приходится иметь дело с многозначными числами. Как и другие выборочные показатели, корреляционное отношение является оценкой своего генерального параметра и, как величина случайная, сопровождается ошибкой, определяемой по формуле
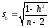 . (12)
. (12)
Достоверность оценки корреляционного отношения можно проверить по t-критерию Стьюдента. H0-гипотеза исходит из предположения, что генеральный параметр равен нулю, т.е. должно выполнятся следующее условие:
 (13)
(13)
для
числа степеней свободы
 и уровня значимостиα.
и уровня значимостиα.
Коэффициент
детерминации.
Для истолкования значений, принимаемых
показателями тесноты корреляционной
связи, используют коэффициенты
детерминации,
которые показывают, какая доля вариации
одного признака зависит от варьирования
другого признака. При наличии линейной
связи коэффициентом детерминации служит
квадрат коэффициента корреляции R2xy,
а при нелинейной зависимости между
признаками y
и x
– квадрат корреляционного отношения
h2yx.
Коэффициенты детерминации дают основание
построить следующую примерную шкалу,
позволяющую судить о тесноте связи
между признаками: при
 связь считается средней;
связь считается средней; указывает на слабую связь и лишь при
указывает на слабую связь и лишь при можно судить о сильной связи, когда
около 50 % вариации признакаY
зависит от вариации признака X.
можно судить о сильной связи, когда
около 50 % вариации признакаY
зависит от вариации признака X.
Оценка
формы связи.
При строго линейной зависимости между
переменными величинами y
и x
осуществляется равенство
 .
В таких случаях коэффициенты корреляционного
отношения совпадают со значением
коэффициента корреляции. Совпадут при
этом по своему значению и коэффициенты
детерминации, т.е.
.
В таких случаях коэффициенты корреляционного
отношения совпадают со значением
коэффициента корреляции. Совпадут при
этом по своему значению и коэффициенты
детерминации, т.е. .
Следовательно, по разности между этими
величинами можно судить о форме
корреляционной зависимости между
переменнымиy
и x:
.
Следовательно, по разности между этими
величинами можно судить о форме
корреляционной зависимости между
переменнымиy
и x:
 . (14)
. (14)
Очевидно, что при линейной связи между переменными y и x показатель γ будет равен нулю; если же связь между переменными y и x нелинейная, γ > 0.
Показатель γ является оценкой генерального параметра и, как величина случайная, нуждается в проверке достоверности. При этом исходят из предположения о том, что связь между величинами y и x линейна (нулевая гипотеза). Проверить эту гипотезу позволяет F-критерий Фишера:
 , (15)
, (15)
где
a
– численность групп, или классов
вариационного ряда; N – объем выборки.
Нулевую гипотезу отвергают, если
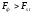 для
для (находят по горизонтали табл.2 Приложений),
(находят по горизонтали табл.2 Приложений), (находят в первом столбце той же таблицы)
и принятого уровня значимостиα.
(находят в первом столбце той же таблицы)
и принятого уровня значимостиα.
