
Лекция 2 конспект
.docxЛекция 2. Умножение вектора на число. Теорема о коллинеарных векторах. Линейная зависимость векторов и ее свойства.
Литература. [1] § 5, 6.
Определение 3.
Под произведением ненулевых числа
и вектора
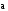 понимается такой вектор
понимается такой вектор ,
который удовлетворяет следующим
условиям:
,
который удовлетворяет следующим
условиям:
-
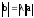 , где
, где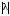 - абсолютная величина .
- абсолютная величина . -
Если > 0 , то векторы
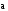 и
и
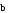 сонаправлены; если
< 0 , то
сонаправлены; если
< 0 , то
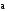 и
и
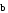 противоположно направлены.
противоположно направлены.
В случае, когда
= 0,или
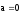 ,произведение
,произведение
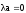 .
.
Рассмотрим свойства операции произведения вектора на число.
Свойство
1. Пусть
 - произвольный вектор, тогда
- произвольный вектор, тогда
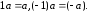
Первое
равенство непосредственно следует из
определения 1. Для доказательства второго
достаточно проверить, что векторы
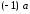 и
и
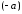 имеют равные модули и одинаковые
направления. Проверьте самостоятельно.
имеют равные модули и одинаковые
направления. Проверьте самостоятельно.
Свойство
2. Для любых чисел
и и любого
вектора
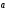 справедливо равенство:
справедливо равенство:
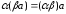 .
.
Доказательство.
Если среди чисел
и есть хотя бы одно,
равное нулю, либо вектор
 - нулевой, то
- нулевой, то
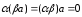 .
В этом случае равенство истинно.
Предположим, что
.
В этом случае равенство истинно.
Предположим, что
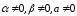 .
Введем обозначения:
.
Введем обозначения:
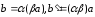 .
Для доказательства свойства достаточно
проверить, что
.
Для доказательства свойства достаточно
проверить, что
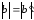 и
и
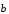
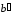 .
.
Из
определения следует:
 ,
,
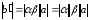 ,
поэтому
,
поэтому
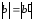 .
Пусть числа и
имеют одинаковые знаки. Тогда
> 0, поэтому
.
Пусть числа и
имеют одинаковые знаки. Тогда
> 0, поэтому

 .
С другой стороны, если
> 0 и > 0, то
.
С другой стороны, если
> 0 и > 0, то
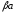
 и
и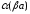
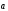 .
При условии, когда
.
При условии, когда
 ,
получим
,
получим
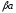
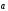 и
и
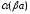
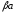 ,
т.е.
,
т.е.
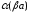
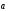 .
Мы показали, что в этом случае
.
Мы показали, что в этом случае
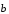
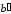 .
.
Если
числа и
имеют разные знаки, то
< 0. Отсюда следует, что
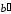
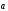 .
Пусть <0, а >0.
Тогда
.
Пусть <0, а >0.
Тогда
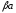
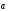 ,
,
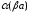
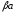 ,
т.е.
,
т.е.
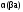
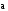 .
Если >0, а <0,
то
.
Если >0, а <0,
то
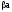
 ,
,
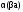
 .
Отсюда вытекает, что
.
Отсюда вытекает, что

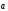 .
Таким образом, и вектор
.
Таким образом, и вектор
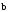 ,
и вектор
,
и вектор
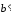 противоположно направлены вектору
противоположно направлены вектору
 ,
поэтому они сонаправлены. Свойство
доказано.
,
поэтому они сонаправлены. Свойство
доказано.
Свойство
3. Для любых чисел
и и любого
вектора
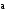 справедливо равенство:
справедливо равенство:
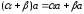 .
.
Доказательство.
Пусть
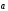 =
=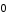 .
Тогда и левая, и правая части равенства
равны нулевому вектору. Если
= 0 или = 0, то, очевидно,
равенство выполнено, Будем предполагать,
что
.
Тогда и левая, и правая части равенства
равны нулевому вектору. Если
= 0 или = 0, то, очевидно,
равенство выполнено, Будем предполагать,
что
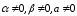 .
.
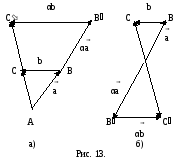
1. Пусть
> 0, > 0. В этом
случае
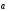 ,
,
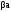
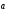 .
Отложим от точки А вектор
.
Отложим от точки А вектор
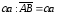 ,
затем от точки В - вектор
,
затем от точки В - вектор
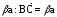 (рис. 13, а). Тогда
(рис. 13, а). Тогда
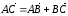 .
Так как > 0 и
> 0, то точка В лежит между А и
С. Поэтому
.
Так как > 0 и
> 0, то точка В лежит между А и
С. Поэтому
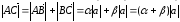 ,
,

 .
С другой стороны, +
> 0, отсюда
.
С другой стороны, +
> 0, отсюда

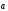 .
Таким образом, вектор
.
Таким образом, вектор
 равен
по длине и сонаправлен с
равен
по длине и сонаправлен с
 .
Следовательно,
.
Следовательно,
 =
=
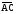 =
=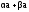 .
В этом случае равенство (2.2) доказано.
.
В этом случае равенство (2.2) доказано.
2. Пусть
< 0, < 0. Тогда

 ,
,

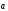 .
Отложим от точки А вектор
.
Отложим от точки А вектор
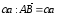 ,
затем от точки В отложим вектор
,
затем от точки В отложим вектор
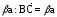 (рис.13, б). Тогда
(рис.13, б). Тогда
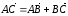 и
и
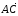
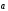 .
Так как векторы
.
Так как векторы
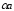 и
и
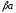 сонаправлены, то точка В лежит между
А и С. Поэтому
сонаправлены, то точка В лежит между
А и С. Поэтому
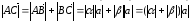 .
В силу того, что и
отрицательные
числа,
.
В силу того, что и
отрицательные
числа,
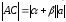 .
Определим длину и направление вектора
.
Определим длину и направление вектора
 .
В рассматриваемом случае +
< 0, следовательно,
.
В рассматриваемом случае +
< 0, следовательно,

 ,
,
 .
Таким образом, длины и направления
векторов
.
Таким образом, длины и направления
векторов
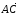 и
и
 совпадают.
совпадают.
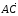 =
=
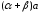 =
= .
В этом случае равенство (2.2) доказано.
.
В этом случае равенство (2.2) доказано.
Предположим, что и имеют различные знаки. Без ограничения общности можно считать, что > 0, а < 0.
3. Пусть
> 0, < 0, и
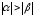 .
Тогда
.
Тогда
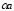
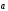 ,
,
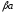
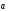 .
Отложим от точки А вектор
.
Отложим от точки А вектор
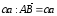 ,
затем от точки В отложим вектор
,
затем от точки В отложим вектор
 (рис.13, в).
(рис.13, в).
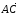 =
= .
Так как
.
Так как
 ,
то точка С лежит между А и В.
Поэтому
,
то точка С лежит между А и В.
Поэтому
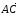
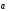 ,
,
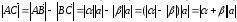 .
С другой стороны, +
> 0, следовательно,
.
С другой стороны, +
> 0, следовательно,

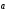 .
.
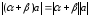 .
Векторы
.
Векторы
 и
и
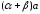 имеют одинаковые длины и направления.
Равенство (2.2) для этого случая также
доказано.
имеют одинаковые длины и направления.
Равенство (2.2) для этого случая также
доказано.
4. Пусть
> 0, < 0, и
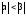 .
Отложим от точки А вектор
.
Отложим от точки А вектор
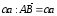 ,
затем от точки В отложим вектор
,
затем от точки В отложим вектор
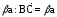 (рис.13, г).
(рис.13, г).
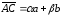 .
В этом случае точка А лежит между
точками В и С. Поэтому
.
В этом случае точка А лежит между
точками В и С. Поэтому
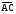
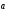 ,
,
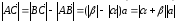 .
Но в рассматриваемом случае +<0.
Следовательно,
.
Но в рассматриваемом случае +<0.
Следовательно,
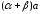
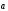 .
Так как
.
Так как
 ,
то длины и направления векторов
,
то длины и направления векторов
 и
и
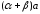 совпадают. Таким образом, для данного
случая
совпадают. Таким образом, для данного
случая
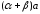 =
=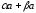 .
.
5. В последнем
случае осталось лишь предположить, что
> 0,
< 0 и +
= 0. Тогда
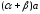 =
=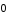 .
Покажем, что
.
Покажем, что
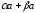 также совпадает с нулевым вектором.
Действительно, =
-, поэтому векторы
также совпадает с нулевым вектором.
Действительно, =
-, поэтому векторы
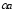 и
и
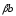 противоположные и их сумма равна нулевому
вектору. Таким образом, и в этом последнем
случае равенство (2.2) доказано.
противоположные и их сумма равна нулевому
вектору. Таким образом, и в этом последнем
случае равенство (2.2) доказано.
Прежде чем приступить к изложению последнего, четвертого свойства операции произведения вектора на число, докажем теорему о коллинеарных векторах.
Теорема
1. (теорема о коллинеарных
векторах). Пусть даны векторы
 и
и
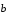 ,
причем
,
причем
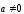 .
Они коллинеарны в том и только в том
случае, когда существует такое число
., для которого
.
Они коллинеарны в том и только в том
случае, когда существует такое число
., для которого
 .
Число
определяется единственным образом.
.
Число
определяется единственным образом.
Доказательство.
Если
 ,
то коллинеарность векторов
непосредственно следует из определения
3.
,
то коллинеарность векторов
непосредственно следует из определения
3.
Обратно.
Пусть

 .
Докажем, что существует требуемое число
. В случае
сонаправленности векторов
.
Докажем, что существует требуемое число
. В случае
сонаправленности векторов
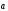 и
и
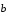 положим
положим
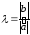 .
В частности, если
.
В частности, если
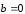 ,
то =0. Если
,
то =0. Если
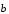
 ,
то будем считать, что:
,
то будем считать, что:
 .
Легко показать, что
удовлетворяет требуемому условию.
Действительно,
.
Легко показать, что
удовлетворяет требуемому условию.
Действительно,
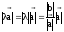 .
Если =0, то
.
Если =0, то
 .
Если > 0, то
.
Если > 0, то

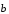 ,
поэтому векторы
,
поэтому векторы
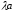 и
и
 сонаправлены и имеют одинаковую длину,
следовательно, они совпадают. Если <0,
то
сонаправлены и имеют одинаковую длину,
следовательно, они совпадают. Если <0,
то
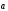
 .
Но
.
Но
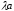
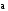 ,
отсюда вытекает, что
,
отсюда вытекает, что

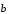 .
В этом случае векторы
.
В этом случае векторы
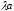 и
и
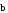 также имеют одинаковые длины и направления.
Таким образом,
также имеют одинаковые длины и направления.
Таким образом,
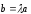 .
.
Докажем
единственность существования числа .
Пусть существуют два числа
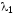 и
и
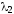 ,
удовлетворяющие условию
,
удовлетворяющие условию
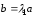 и
и
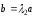 .
Тогда
.
Тогда
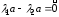 .
Используя соотношения (2.1) и (2.2), получаем:
.
Используя соотношения (2.1) и (2.2), получаем:
 .
Таким образом,
.
Таким образом,
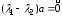 .
Так как
.
Так как
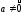 ,
то
,
то
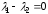 ,
т.е.
,
т.е.
 .
Теорема доказана.
.
Теорема доказана.
Если
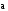 и
и
 нулевые векторы, то при любом
справедливо равенство:
нулевые векторы, то при любом
справедливо равенство:
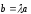 .
.
Докажем последнее свойство операции произведения вектора на число.
Свойство
4. Для любого числа
и любых векторов
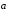 и
и
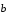 справедливо равенство:
справедливо равенство:
 .
.
Доказательство.
Если = 0, то равенство
(2.3) очевидно. В дальнейшем будем
предполагать, что
0. Пусть
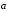
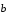 .
Тогда из теоремы о коллинеарных векторах
следует, что
.
Тогда из теоремы о коллинеарных векторах
следует, что
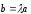 .
Преобразуем правую и левую части
равенства:
.
Преобразуем правую и левую части
равенства:
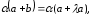

В
этом случае
 .
.
Далее
будем предполагать, что вектор
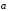 не коллинеарен
не коллинеарен
 .
Пусть >0. Тогда
векторы
.
Пусть >0. Тогда
векторы 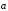 и
и 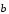 сонаправлены с
сонаправлены с
 и
и
 .
Отложим от точки А векторы
.
Отложим от точки А векторы
 и
и  :
:
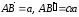 ,
а от точек В и В
векторы
,
а от точек В и В
векторы
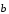 и
и  :
:
 (рис.13, а). Докажем, что треугольники АВС
и AВC
подобны между собой. Действительно,
ABC=ABC,
так как вектор
(рис.13, а). Докажем, что треугольники АВС
и AВC
подобны между собой. Действительно,
ABC=ABC,
так как вектор
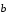 сонаправлен с
сонаправлен с
 ,
то
,
то
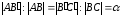 .
Треугольники подобны, так как равны их
углы и прилежащие стороны пропорциональны.
Отсюда следует, что
.
Треугольники подобны, так как равны их
углы и прилежащие стороны пропорциональны.
Отсюда следует, что
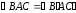 ,
т.е. точки А, С и Сʹ лежат на
одной прямой. Получим:
,
т.е. точки А, С и Сʹ лежат на
одной прямой. Получим:
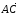
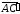 .
Кроме того, из подобия треугольников
вытекает
.
Кроме того, из подобия треугольников
вытекает
 .
Таким образом,
.
Таким образом,
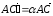 .
Но
.
Но
 ,
поэтому
,
поэтому
 .
Для рассматриваемого случая равенство
(2.3) доказано.
.
Для рассматриваемого случая равенство
(2.3) доказано.
Предположим
теперь, что <0.
Тогда
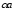
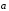 ,
,

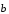 .
Отложим векторы
.
Отложим векторы
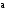 и
и
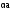 от точек А и А:
от точек А и А:
 ,
а от точек В и В
векторы
,
а от точек В и В
векторы
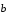 и
и 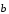 :
:
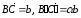 (рис.14, б). Так же, как и в предыдущем
случае, доказывается подобие треугольников
АВС и АВC.
Из их подобия следует, что BAC
= BAC.
Так как векторы
(рис.14, б). Так же, как и в предыдущем
случае, доказывается подобие треугольников
АВС и АВC.
Из их подобия следует, что BAC
= BAC.
Так как векторы
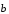 и
и
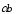 противоположно направлены, то углы ВАС
и BAC
вертикальные. Поэтому точки C,
A и С лежат на одной прямой. Из
подобия треугольников следует, что
противоположно направлены, то углы ВАС
и BAC
вертикальные. Поэтому точки C,
A и С лежат на одной прямой. Из
подобия треугольников следует, что
 .
Векторы
.
Векторы
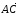 и
и
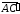 противоположно направлены, следовательно
противоположно направлены, следовательно
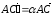 .
С другой стороны,
.
С другой стороны,
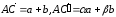 .
Таким образом,
.
Таким образом,
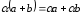 .
Равенство (2.3) доказано полностью.
.
Равенство (2.3) доказано полностью.
Условимся вектор
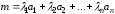 называть линейной комбинацией векторов
называть линейной комбинацией векторов
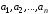 с коэффициентами
с коэффициентами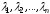 .
В этом случае будем также говорить, что
вектор
.
В этом случае будем также говорить, что
вектор
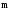 линейно выражается через векторы
линейно выражается через векторы
 с коэффициентами
с коэффициентами
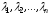 или линейно раскладывается по этим
векторам с указанными коэффициентами.
или линейно раскладывается по этим
векторам с указанными коэффициентами.
Определение
1. Система векторов
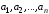 называется линейно зависимой, если
существуют такие числа
называется линейно зависимой, если
существуют такие числа
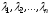 ,
среди которых, по крайней мере, одно
отлично от нуля, что линейная комбинация
,
среди которых, по крайней мере, одно
отлично от нуля, что линейная комбинация
 равна нулевому вектору.
равна нулевому вектору.
Если
система векторов не является линейно
зависимой, то она называется линейно
независимой. Таким образом, система
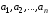 линейно независима в том и только в том
случае, когда из равенства
линейно независима в том и только в том
случае, когда из равенства
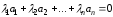 следует:
следует:

Докажем некоторые свойства линейно зависимых систем векторов,
Свойство 1. Если система содержит нулевой вектор, то она линейно зависима.
Доказательство.
Без ограничения общности можно
считать, что
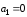 .
Положим
.
Положим
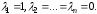 Тогда
Тогда
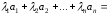
 Мы получили нулевую линейную комбинацию
векторов
Мы получили нулевую линейную комбинацию
векторов
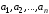 ,
среди коэффициентов которых
,
среди коэффициентов которых
 отлично от нуля. Утверждение доказано.
отлично от нуля. Утверждение доказано.
Свойство
2. Если в системе векторов
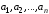 содержится линейно зависимая подсистема,
то вся система также линейно зависима.
содержится линейно зависимая подсистема,
то вся система также линейно зависима.
Доказательство.
Перенумеруем векторы системы так, чтобы
линейно зависимую подсистему составляли
первые k векторов. Таким образом,
существуют числа
 ,
среди которых находится по, крайней
мере, одно отлично от нуля, такие, что
,
среди которых находится по, крайней
мере, одно отлично от нуля, такие, что
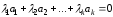 .
Положим
.
Положим
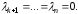 Тогда линейная комбинацию векторов
Тогда линейная комбинацию векторов
 с коэффициентами
с коэффициентами
 равна нулевому вектору:
равна нулевому вектору:
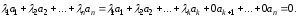 Утверждение доказано.
Утверждение доказано.
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из ее векторов линейно выражается через остальные.
Доказательство.
Необходимость. Пусть система векторов
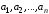 линейно зависима. Тогда существуют
числа
линейно зависима. Тогда существуют
числа
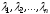 ,
среди которых содержится, по крайней
мере, одно, отличное от нуля, для которых
,
среди которых содержится, по крайней
мере, одно, отличное от нуля, для которых
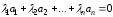 .
Перенумеруем векторы и числа так, чтобы
.
Перенумеруем векторы и числа так, чтобы
 .
Тогда
.
Тогда
 Разделим обе части этого равенства на
ненулевое число
Разделим обе части этого равенства на
ненулевое число
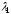 :
:
 Вектор
Вектор
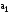 представлен как линейная комбинация
векторов
представлен как линейная комбинация
векторов
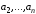 с коэффициентами
с коэффициентами
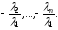 Необходимость доказана.
Необходимость доказана.
Достаточность. Пусть один из векторов
системы, например
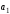 ,
линейно выражается через остальные:
,
линейно выражается через остальные:
 Тогда
Тогда
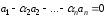 .
Мы получили нулевую линейную комбинацию
векторов
.
Мы получили нулевую линейную комбинацию
векторов
 с коэффициентами
с коэффициентами
 ,
среди которых содержится число 1, отличное
от нуля Система
,
среди которых содержится число 1, отличное
от нуля Система
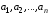 линейно зависима. Утверждение доказано.
линейно зависима. Утверждение доказано.
Из рассмотренных свойств вытекает, что линейно независимая система векторов не содержит нулевого вектора, любая ее подсистема также линейно независима, и ни один из ее векторов линейно не выражается через остальные.
Понятие линейной зависимости было введено нами «алгебраическим» способом. Но в аналитической геометрии с каждым «алгебраическим» свойством геометрических объектов имеет геометрический смысл. Установим его для линейно зависимых систем векторов. Теорема о коллинеарных векторах позволяет выяснить этот смысл для линейной зависимой системы, состоящей из двух векторов.
Теорема 1. Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство.
Пусть
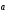 ||
||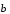 .
Тогда из теоремы о коллинеарных векторах
(см. § 2) следует,
что один из векторов, например
.
Тогда из теоремы о коллинеарных векторах
(см. § 2) следует,
что один из векторов, например
 ,
линейно выражается через вектор
,
линейно выражается через вектор
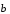 :
:
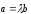 .
Из свойства 3 настоящего параграфа
следует, что система
.
Из свойства 3 настоящего параграфа
следует, что система
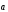 ,
,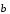 линейно зависима.
линейно зависима.
Обратно.
Пусть
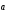 ,
,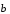 линейно зависимая система векторов.
Тогда из того же свойства 3 имеем: один
из векторов, например
линейно зависимая система векторов.
Тогда из того же свойства 3 имеем: один
из векторов, например
 ,
линейно выражается через второй:
,
линейно выражается через второй:
 .
Поэтому векторы коллинеарны. Теорема
доказана.
.
Поэтому векторы коллинеарны. Теорема
доказана.
Следствие. Система, состоящая из двух неколлинеарных векторов, линейно независима.
Будем
говорить, что вектор
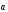 параллелен плоскости
параллелен плоскости
 ,
если его представитель параллелен или
лежит в этой плоскости. Ясно, что это
определение не зависит от выбора
представителя вектора.
,
если его представитель параллелен или
лежит в этой плоскости. Ясно, что это
определение не зависит от выбора
представителя вектора.
Определение
2. Система векторов называется компланарной, если существует
плоскость, которой параллельны все
векторы системы.
называется компланарной, если существует
плоскость, которой параллельны все
векторы системы.
Приведем примеры компланарных систем векторов.
1.
Если система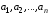 .
состоит из коллинеарных векторов, то
она компланарная.
.
состоит из коллинеарных векторов, то
она компланарная.
Действительно, согласно определению коллинеарных векторов, существует прямая а, параллельная представителям данных векторов. Возьмем произвольную плоскость, параллельную прямой а. Тогда векторы параллельны выбранной плоскости.
2. Система, состоящая из двух векторов, всегда является компланарной.
В самом деле,
рассмотрим векторы
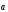 и
и
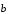 .
Если
.
Если
 ||
||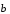 ,
то справедливость утверждения вытекает
из предыдущего примера. Если они
неколлинеарны, то отложим их от некоторой
точки А:
,
то справедливость утверждения вытекает
из предыдущего примера. Если они
неколлинеарны, то отложим их от некоторой
точки А:
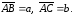 Точки А, В и С не лежат на
одной прямой, поэтому существует
проходящая через них плоскость. Векторы
Точки А, В и С не лежат на
одной прямой, поэтому существует
проходящая через них плоскость. Векторы
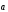 и
и
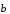 параллельны этой плоскости.
параллельны этой плоскости.
