Теория множеств задания(1,4)

В качестве проверки изученного материала необходимо выполнить задания:

Задание 1. Определите результат операции:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

Задание 2. Докажите тождество

Докажите тождество AUB=AU(B\A).

РЕШЕНИЕ: Чтобы доказать это тождество, нужно показать, что каждый элемент первого

множества принадлежит второму и наоборот, то есть эти множества совпадают.

Пусть x∈AUB, то есть x∈A или x∈B. Если x∈A, то x∈AU(B\A). Если x∉A, но x∈B, то

x∈B\A, следовательно, x∈AU(B\A).

Пусть x∈AU(B\A), то есть x∈A или x∈B\А. Если x∈A, то x∈AUB. Если x∈В, но x∉A

(x∈B\А), то x∈AUB.

Задание 3. Определите свойства следующих отношений:

1. «прямая x пересекает прямую y» (на множестве прямых)

2. «число x больше числа y на 2» (на множестве натуральных чисел)

3. «число x делится на число y без остатка» (на множестве натуральных чисел)

4. «x - сестра y» (на множестве людей).

РЕШЕНИЕ:

1. xRy=«прямая x пересекает прямую y» (на множестве прямых).

Это отношение:

Рефлексивное, так как «прямая x пересекает прямую x» выполняется для любой прямой

(она пересекает себя в каждой точке);

Симметрическое, так как из того, что «прямая x пересекает прямую y» следует, что

«прямая y пересекает прямую x» для любых прямых x,y;

Также можно заметить, что это отношение не является тождественным, транзитивным и

полным.

2. xRy=«число x больше числа y на 2» (на множестве натуральных чисел).

Это отношение:

Антирефлексивное, так как ни для одного элемента из множества натуральных чисел не

выполняется «число x больше числа x на 2»;

Антисимметрическое, так как для любых элементов x,y из множества натуральных чисел

из того, что «число x больше числа y на 2» следует невыполнение того, что «число y

больше числа x на 2»;

Также можно заметить, что это отношение не является тождественным, транзитивным и

полным.

3. xRy=«число x делится на число y без остатка» (на множестве натуральных чисел).

Это отношение:

Рефлексивно, так как для любого элемента x из множества натуральных чисел

выполняется «число x делится на число x без остатка»;

Тождественно, так как для любых элементов x,y из множества натуральных чисел из

того, что «число x делится на число y без остатка» и «число y делится на число x без

остатка», следует, что x=y;

Транзитивное, так как для любых элементов x,y,z из множества натуральных чисел из

того, что «число x делится на число y без остатка» и «число y делится на число z без

остатка», следует, что «число x делится на число z без остатка»;

Также можно заметить, что это отношение не является симметрическим,

антисимметрическим и полным. Это отношение является отношением порядка.

4. xRy=«x – сестра y» (на множестве людей)

Это отношение:

Антирефлексивно, так как для любого человека x неверно, что «x – сестра x»;

Транзитивно, так как для любых людей x, y, z таких что «x – сестра y» и «y – сестра z»

следует, что «x – сестра z» .

Также можно заметить, что это отношение не является симметрическим,

антисимметрическим, тождественным и полным.

Задание 4. Дано множество и его подмножества , , . Докажите, что такое разбиение соответствует некому отношению эквивалентности на этом множестве, т.е. данные подмножества можно назвать классами эквивалентности. Постройте факто-множество (множество, состоящее их классов эквивалентности).

Решения оформить в электронном виде и отправить по адресу: MAEjova@mesi.ru

Если возникают вопросы, то задавайте их на форуме в Виртуальном Кампусе или отсылайте на почту.

Множество (определение, конечность, мощность, пример)

Множество – это совокупность элементов объединенных некоторым признаком или свойствами.

Конечное множество состоит из конечного числа элементов.

например, множество страниц в книге…

Бесконечное множество состоит из бесконечного числа элементов, т.е. это множество, которое не является ни конечным, ни пустым.

Например: множество действительных чисел, множество точек плоскости, множество атомов во Вселенной и т.д.

Мощностью конечного множества называется количество его элементов. Мощность множества Aобозначается m (A).

Способы задания множеств

1. Перечисление элементов. Элементы заключаются в фигурные скобки.

M = {a1, a2, . . . , ak}

2. Порождающей процедурой. Указывается способ получения новых элементов из уже

имеющихся.

3. С помощью характеристического предиката. Предикат описывает свойство всех эле-

ментов, входящих в множество.M = {x : P(x)} или M = {x|P(x)}

Пример

1. N = {0, 1, 2, 3, . . . }

2. 1 ∈ M; если a ∈ M, то 2 · a ∈ M

3. M = {x : x ∈ N ∧ x < 10}

Операции над множествами (описание, примеры)

Суммой, или объединением произвольного конечного или бесконечного множества множеств

называется множество,состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множествА,В.

Пересечением любого конечного или бесконечного множества множеств

называется множество, состоящее из тех и только тех элементов, которые принадлежат множествам А и В одновременно.

Разностью между множеством В и множеством А

называется множество всех элементов из В , не являющихся элементами из А .

Дополнением множества А в В

называется разность А\В, если В является подмножеством множества А.

1. Объединение A ∪ B = {x|x ∈ A ∨ x ∈ B}

2. Пересечение A ∩ B = {x|x ∈ A ∧ x ∈ B}

3. Разность A \ B = {x|x ∈ A ∧ x 6∈ B}

4. Дополнение A = {x|x ∈ U ∧ x 6∈ A}

5. Симметрическая разность

A 4 B = {x|(x ∈ A ∧ x 6∈ B) ∨ (x ∈ B ∧ x 6∈ A)}

Прямое (декартовое) произведение (определение, пример)

Прямое или декартово произведение — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только втеории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры существующие на перемножаемых множествах.

Бинарные отношения (определение, бинарное отношение на множестве, отношение к декартовому произведению)

В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется непустое множество упорядоченных пар элементов этого множества.

В математике большую роль играют бинарные отношения, т.е. отношения, заданные на декартовом произведении двух множеств .

•  называют бинарным отношением на множестве , если . При этом вместо записи  часто используют запись 

• Если  то говорят, что  определено на паре множеств 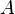 и .

• Множество всех первых элементов пар из  называется областью определения отношения  и обозначается как .

• Множество всех вторых элементов пар из  называется областью значения отношения  и обозначается как .

• Инверсия(Обратное отношение)  — это множество  и обозначается, как .

• Композиция (суперпозиция) бинарных отношений  и  — это множество  и обозначается, как .

Свойства бинарных отношений

Бинарные отношения могут обладать различными свойствами, такими как

• Рефлексивность .

• Антирефлексивность (иррефлексивность): .

• Симметричность: .

• Антисимметричность: .

• Транзитивность: .

• Асимметричность: . Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Матрица бинарного отношения (определение, пример)

Бинарная матрица (двоичная матрица, (0, 1)-матрица) — матрица, элементами которой являются 0 или 1.

 — бинарная матрица 

• Матрица перестановки — бинарная матрица, в каждом столбце и строке которой лишь одна единица, а все остальные элементы — 0.

• В теории графов, матрицей смежности простого графа называется бинарная матрица, на пересечении -ой строки и 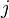-го столбца которой стоит 1, если вершины  соединены ребром (или дугой) и 0 в противном случае. Матрица достижимости орграфа также является бинарной матрицей.

Отношение эквивалентности (определение, класс эквивалентности)

Отношение  на множестве  называетсяотношением эквивалентности, если оно обладает следующими свойствами:

1.  для всех  (рефлексивность)

2. Если , то  (симметричность)

3. Если  и , то  (транзитивность)

Обычно отношение эквивалентности обозначают знаком  или  и говорят, что оно (отношение) задано на множестве  (а не на ). Условия 1-3 в таких обозначениях выглядят более естественно:

1.  для всех  (рефлексивность)

2. Если , то  (симметричность)

3. Если  и , то  (транзитивность)

Свойства классов эквивалентности

4.  для всех  (рефлексивность)

5. Если , то  (симметричность)

6. Если  и , то  (транзитивность)

Фактор-множество (определение, пример)

Совокупность всех классов эквивалентности называется фактор-множеством. Оно обозначается символом X/R.

Дискретная математика: Конспект лекций. Ч.1 Автор: Шишмарев Ю.Е. Редактор: Александрова Л.И.

http://abc.vvsu.ru/Books/discr_ma/default.asp

Для рассмотрения подходят все параграфы главы 2 (Введение в теорию множеств), кроме пятого и девятого (их можно прочитать для общего ознакомления).

Список вопросов для подготовки:

1. Множество (определение, конечность, мощность, пример)

2. Способы задания множеств

3. Операции над множествами (описание, примеры)

4. Прямое (декартовое) произведение (определение, пример)

5. Бинарные отношения (определение, бинарное отношение на множестве, отношение к декартовому произведению)

6. Свойства бинарных отношений

7. Матрица бинарного отношения (определение, пример)

8. Отношение эквивалентности (определение, класс эквивалентности)

9. Свойства классов эквивалентности

10. Фактор-множество (определение, пример)

Дополнительная литература:

1) Набор слайдов по курсу «Основы теории множеств» http://anisimovdmitry.com/Documents/MathLogicCourse/settheory.pdf

(красочный проект с доступной формой организации информации, но имеется много дополнительных сведений)

2) Аминова А.В. Элементы теории множеств. // Казанский государственный университет, физический факультет. – Казань, 2008.

http://www.ksu.ru/f6/k6/bin_files/teoriya_mnoghestv!4.pdf

Учитывая структуру курса, то читать стоит следующие страницы: Лекция 1. Раздел 2 [стр. 9-15], Лекция 2. Разделы 1-3 [стр. 16-25], Лекция 3. Разделы 2-3 [стр. 29-33], Лекция 4.Раздел 1 [стр. 34-35]

(понятное изложение, большое число графических изображений для описания нововведенных понятий)