
ЭВМ_Семестр3_МетодПособие
.pdf"ПОЛИНОМ", "Лист1!$E$" & 2 & ":$E$" & (M + 2), "Лист1!$F$" & 2 & ":$F$" & (M + 2), _
"УЗЛЫ", "Лист1!$A$" & 2 & ":$A$" & (N + 2), "Лист1!$B$" & 2 & ":$B$" & (N + 2))
End Sub
' Интерполяционный полином в компактном виде: P(x)=x^2*(X^2-1 ) /6
Function POL(ByVal x As Double) As Double
POL = x ^ 2 * (x ^ 2 - 1) / 6
End Function
После запуска программы вводят значение N, например, для получения графиков к заданию 1 следует задать число 4. Для получения графиков при другом значении N следует удалить ранее нарисованную диаграмму и снова запустить программу.
4.2.2 Тексты и варианты заданий
Задание 1.
а) По заданным узлам записать полином Лагранжа и представить его в удобном для вычисления компактном виде.
б) Построить на одной диаграмме график вычисляемого с помощью функции PLagr полинома Лагранжа и полученного в пункте а) полинома в компактном виде. На диаграмме показать узлы интерполяции.
в) Определить значения первых производных в концевых точках полинома из пункта а), и по ним и узловым точкам определить производные кубического сплайна во всех узловых точках (см. пример 4.2).
г) Построить на одной диаграмме график интерполяционного полинома и кубического сплайна. Расчѐт ординат сплайна с заданными производными в узлах можно выполнить с помощью функции HconS при Kod=1. На диаграмме показать маркерами узлы интерполяции.
Задание 2.
Интерполировать полиномом и кубическим сплайном n=N+1 равномерно расположенных на отрезке [x1; x5] узловых точек с ординатами, равными округлѐнным до десятых значениями интерполирующего полинома, полученного в предыдущем задании. Проследить на графиках поведение приближающих функций при различных
81

N (4<N<22). Сделать выводы о возможностях и границах применения интерполяции сплайнами и полиномами.
Указание. Использовать программу примера, предварительно скорректировав еѐ под свои данные и полином, интерполирующий исходные точки данных.
Задание 3. Для контроля перенести в MATLAB массивы узловых точек (x, y) и массив ординат насчитанных точек Xi (или насчитать их в MATLAB в том же или большем количестве). Вычислить в MATLAB ординаты Yi интерполирующего кубического сплайна по инструкции
YSi = spline(x, y, Xi); |
|
% сплайн c условиями «без узла» |
|
|||||||||||||
YPi = polyval(polyfit(x, y, N), Xi); |
% N задать числом |
|
||||||||||||||
и показать на графике узловые точки, сплайн и полином: |
|
|
|
|
||||||||||||
plot(Xi,YSi, Xi,YPi, x,y,'ro') |
|
|
|
|
|
|
|
|||||||||
Таблица 4.1 Варианты заданий |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
i= |
1 |
2 |
3 |
4 |
|
5 |
|
N |
i |
1 |
2 |
3 |
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вар |
xi= |
-2 |
-1 |
0 |
1 |
|
2 |
|
вар |
xi |
-2 |
-1 |
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
yi= |
-2 |
0 |
0 |
0 |
|
2 |
|
16 |
yi= |
-2 |
1 |
0 |
-1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
yi= |
0 |
1 |
0 |
-1 |
|
0 |
|
17 |
yi= |
-2 |
0 |
0 |
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
yi= |
1 |
0 |
0 |
1 |
|
0 |
|
18 |
yi= |
-2 |
1 |
0 |
-1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
yi= |
1 |
1 |
0 |
-1 |
|
-1 |
|
19 |
yi= |
0 |
1 |
0 |
0 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
yi= |
1 |
0 |
-1 |
0 |
|
-1 |
|
20 |
yi= |
-2 |
-2 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
yi= |
1 |
0 |
0 |
0 |
|
-1 |
|
21 |
yi= |
-1 |
0 |
-1 |
0 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
yi= |
0 |
-1 |
0 |
1 |
|
0 |
|
22 |
yi= |
1 |
0 |
-1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
yi= |
1 |
0 |
1 |
0 |
|
-1 |
|
23 |
yi= |
1 |
0 |
0 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
yi= |
0 |
-1 |
0 |
2 |
|
0 |
|
24 |
yi= |
2 |
1 |
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
yi= |
0 |
0 |
0 |
1 |
|
-1 |
|
25 |
yi= |
-1 |
0 |
1 |
0 |
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
yi= |
1 |
2 |
0 |
-2 |
|
-1 |
|
26 |
yi= |
1 |
1 |
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
yi= |
-1 |
0 |
1 |
0 |
|
1 |
|
27 |
yi= |
0 |
1 |
0 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
yi= |
0 |
0 |
0 |
1 |
|
1 |
|
28 |
yi= |
-1 |
0 |
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
yi= |
2 |
-1 |
0 |
1 |
|
-2 |
|
29 |
yi= |
0 |
1 |
0 |
-1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
82
15 |
yi= |
0 |
-2 |
0 |
2 |
0 |
30 |
yi= |
2 |
0 |
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
83
5 РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №5 Приближения по методу наименьших квадратов
5.1Краткие теоретические сведения
Вряде задач коэффициенты, входящие в уравнения, получаются из экспериментальных данных, причѐм по этим данным можно записать m уравнений, и это число m бывает значительно больше числа n неизвестных. В таких случаях не игнорируют избыточные данные, а стараясь учесть всю информацию, заключѐнную в данных, решают так называемые переопределѐнные системы уравнений или, в геометрической трактовке, - задачу сглаживания экспериментальных данных.
5.1.1 Решение переопределённой системы n линейных уравнений с m неизвестными (n > m)
Пример 5.1. Требуется определить (как можно точнее) электри- |
|
|
||||||||||||
ческую проводимость (c) шунта (т.е. резистора с малым сопротивле- |
|
|
||||||||||||
нием), имея в распоряжении амперметр и вольтметр низкого класса |
|
|
||||||||||||
точности. Результаты замеров тока y (в амперах) |
|
Таблица 5.1. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
через шунт в зависимости от подведѐнного напря- |
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
|
1 |
|
2 |
|
3 |
|
|
||||
жения x (в вольтах) отражены в таблице 5.1. |
|
y |
|
|
1 |
|
1 |
|
2 |
|
|
|||
Подставляя в закон Ома y c x |
с единствен- |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
ной (т.е. n=1) неизвестной (c) три пары (т.е. m=3) значений (x, y) , по- |
|
|
||||||||||||
лучаем три соотношения для определения вели- |
|
|
|
|
|
|
|
|
|
|
|
|||
1 с 1 |
|
|
|
|
|
|
|
|||||||
чины c. Это отражено в системе уравнений на |
|
1 |
1 |
|
||||||||||
|
|
|
|
|
||||||||||
|
|
2 c 1 |
|
|||||||||||
|
|
|
|
2 с 1 |
|
|||||||||
рисунке 5.1 |
(и в графике на рисунке 5.3). |
3 с 2 |
|
|
|
|
|
|
||||||
|
3 |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Можно, |
перенеся в левую часть вектор y , |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
F c y |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записать уравнения в виде Fc y |
, добавив |
|
|
Рисунок 5.1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
справа вектор невязок |
- его длина может слу- |
|
|
|
|
|
|
|
|
|
|
|
||
жить мерой несоответствия закону Ома. Длина вектора |
|
|
|
|
|
|
|
|
|
|||||
Fc зависит от величины c; стремятся выбрать такое |
|
|
|
|
|
|
|
|
|
|||||
c c* , чтобы длина вектора невязок была наименьшей. |
|
|
|
|
|
|
|
|
|
|||||
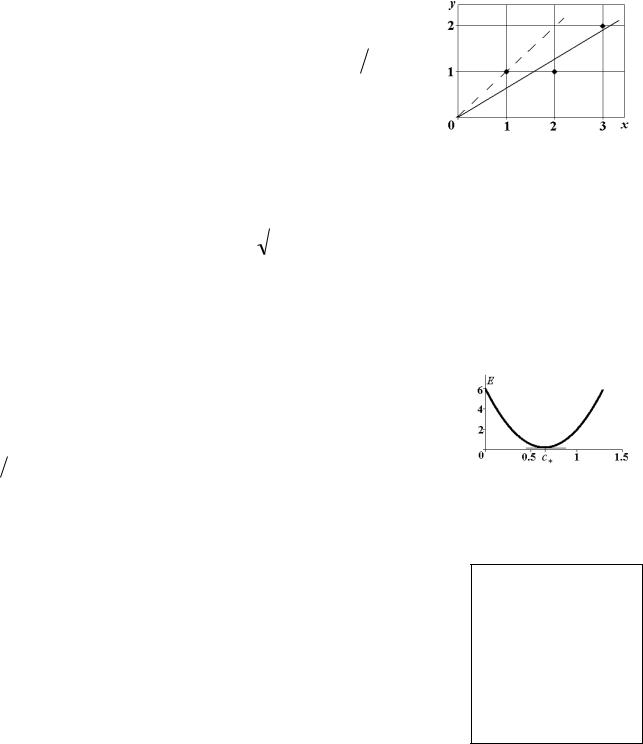
Из геометрических соображений (см. рис. 5.2) следует, |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что при этом вектор |
должен быть перпендикулярен |
|
Рисунок 5.2 |
|
|
|||||||||
вектору Fc* ; для иных положений (они на рисунке по- |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
84 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
казаны пунктиром) длина вектора |
невязок больше. Условие пер- |
|
|
|
|
пендикулярности (нормальности) векторов F и |
Fc y выражает- |
|
ся равенством нулю их скалярного произведения: T или
F Fc y 0
FTFc FTy .
Таким образом, если определить проводимость шунта по первому замеру, то получается c=1/1=1ом-1 (пунктирная
линия на рис. 5.3). А учѐт всех трѐх замеров по
|
|
|
выведенной формуле |
даѐт c* FTy FTF |
|
=(1·1+2·1+3·2)/(12+22+32)=9/14 ом-1 (сплошная |
|
|
линия на рис. 5.3) и более реальный график, от- |
|
|
ражающий связь напряжения и тока. |
Рисунок 5.3. |
|
|
|
|
Решая эту задачу, |
можно было напрямую |
|
записать выражение для квадрата длины вектора невязок (это то, что
|
|
|
|
|
|
|
|
|
|
|
|
|
21 22 23 |
||||
стоит под корнем в длине |
|
|
вектора ): |
|||||
|
|
3 |
|
|
|
|
|
|
E(с) 21 22 23 c xk yk |
2 (1 c 1)2 (2 c 1)2 (3 c 2)2 |
|||||||
|
|
k 1 |
|
|
|
|
|
|
14 c2 18 c2 |
6 |
|
|
|
|
|
|
|
График функции E(c) |
|
показан на рис. 5.4. В |
||||||
точке минимума касательная к графику горизон- |
||||||||
тальна, |
а |
производная |
|
равна |
нулю |
|||
dE dt 2 14 c 18 0 . Из |
этого |
условия значение |
||||||
c* 9 /14 . При этом значении сумма E(c) |
Рисунок 5.4 |
квадратов |
отклонений точек данных от прямой y c x будет наименьшей.
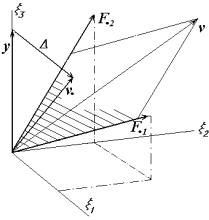
Пример 5.2. Дана переопределѐнная система n ли-
|
|
m |
(n m) неизвест- |
нейных уравнений Fc y с |
|||
ными (см. рис. 5.5). Решить еѐ, т.е. найти такие c1 , c2 , чтобы несоответствие между правой и левой частя-
ми |
уравнений было наименьшим (вектор |
|
|
|
|
Fc y невязок имел минимальную длину).
Fc y
1 с1 0 с2 01 с1 1 с2 01 с1 2 с2 1
Рисунок 5.5
85
Метод решения (метод наименьших квадратов)
Уравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнениями |
наблюдений) |
можно |
|||||||||||||||
F c y (называемые |
|||||||||||||||||||||||||||||||
записать в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 0 |
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 1 |
|
0 |
|
|
|
|
|
c F |
c |
|
|
|||||||||||||||||||
Fc y |
|
1 |
1 c1 |
|
1 |
c2 |
0 |
F |
2 |
y |
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
|
|||||
|
|
|
1 |
2 |
с2 |
|
1 |
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
где |
F |
означает вектор - j-столбец матри- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цы (т.е. первый индекс « » пробегает все |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
значения номеров строк). Изобразим на |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
рис. 5.6 координатную систему, по осям |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
которой будем откладывать каждую из |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
трех координат векторов-столбцов. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F 1 c1 F 2 |
c2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Векторы |
|
|
|
v |
Fc |
при |
|
раз- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
личных c1, c2 лежат в плоскости , |
опре- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
деляемой |
|
векторами |
|
F 1 , F 2 |
. |
|
Вектор |
||||||||||||
|
|
Рисунок 5.6 |
|
|
|
|
|
|
|
|
|
|
- это вектор, |
соединяющий |
|||||||||||||||||
|
|
|
|
|
|
|
Fc |
y |
|||||||||||||||||||||||
концы векторов |
|
|
и |
|
|
|
|
|
|
|
|
|
правила |
сложения |
векторов |
||||||||||||||||
y |
|
|
v (вспомним |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наименьшая? |
||||||
y |
|
v ). При каком |
v (каких c , c |
2 |
) длина вектора |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Очевидно, что кратчайшим расстоянием от конца вектора y до плос-
кости будет перпендикуляр, опущенный из этой точки на плос-
кость. |
Вектор |
* , |
совпадающий с этим перпендикуляром, будет |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
наименьшим, |
и ему соответствует вектор |
v* , |
который совпадет с |
||||||||
проекцией вектора |
|
|
(см. рис. 5.6). |
Естественно, |
|||||||
y на плоскость |
|||||||||||
что лежащий в плоскости , вектор |
|
|
|
|
|
||||||
v* |
перпендикулярен вектору * |
||||||||||
|
|
|
|
|
|
|
|
|
|
запишем, приравняв |
|
. Условие перпендикулярности векторов v и |
|||||||||||
нулю их скалярное произведение (т.к. v |
cos( 900 ) 0 ): |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
vT |
|
(Fc)T (Fc y) (cT FT )(Fc y) cT (FT Fc FT y) 0 . |
|||||||||
|
|
|
|
|
Изначально вектор c 0 , а он должен определяться по точкам дан- |
||||
ных, поэтому |
|
|
|
|
|
|
|
|
|
FT Fc FT y 0 |
FT Fc FT y , |
|||
86

а вектор c* , доставляющий минимум вектору невязок, должен определяться решением нормальной системы уравнений
|
|
|
|
|
|
|
|
|
|
|
|
A FTF , а |
|
|
|
|
|
|
|
|
|
|
|
Ac |
b , где |
b FT y . |
|
|
|
(5.1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0 |
|
|
|
|
|
|
|
|
|
||||
T |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
Ac b |
|
|
|||||
|
1 |
|
1 1 |
3 |
3 |
|
|
|
|
|
|
|
||||||||
A F F |
|
|
|
|
|
; |
|
3 |
3 |
|
с1 |
1 |
|
|||||||
|
0 1 2 |
1 2 |
|
3 |
5 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
5 |
с2 |
2 |
|
|
|
1 |
1 |
1 |
|
|
|
0 |
|
|
1 |
; |
|
|
с1 0,166667 с2 0,5 |
|
|||||
|
|
|
|
|
|
|
||||||||||||||
b FT y |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 5.7 |
|
||||
|
0 |
2 |
1 |
|
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Числовая запись системы (5.1) и еѐ решения дана на рис. 5.7.
Вычисления в Excel показаны на рис. 5.8. Числовые коэффициенты уравнений наблюдений (см. рис. 5.5) помещены в диапазон ячеек B2:D4. Для получения коэффициентов нормальной системы уравнений следует: выделить диапазон ячеек E2:G3, нажать F2, набить формулу: =МУМНОЖ(ТРАНСП(B2:C4);B2:D4). После нажатия клавиш Ctrl+Shift+Enter вычисленные элементы матрицы A=FTF помещаются в диапазон ячеек E2:F3, а вектор b= FTy займѐт диапазон G2:G3. Решение нормальной системы уравнений выполним обращением к функции xCdGauss, определѐнной пользователем (см. таблицу. 2.1). Вычисленные коэффициенты с1* 1 6, с2* 1 2 занесены в ячейки E4:F4 (см. рис. 5.8), а число обусловленности выведено в ячейку G4.
5.1.2 Сглаживание точечных данных
Систему уравнений наблюдений в решѐнном примере 5.2 удобно трактовать как условия с1 1 с2 xk yk проведения прямой с1 1 с2 x y через точки xk , yk , k 1, , 3, а вычисленные неизвестные с1*, с2 * - как коэффициенты в уравнении прямой. В общем случае прямую не удастся провести через три (и более) точки, но требование минимальности длины (или, что равносильно, квадрата длины) вектора невязок обеспечит прохождение прямой вблизи заданных точек. Такие точки часто получаются в результате замеров в экспериментах и являются приближѐнными (содержат случайные погрешности). По-
87
этому рассматриваемая процедура приближения (аппроксимации) осуществляет сглаживание этих экспериментальных данных.
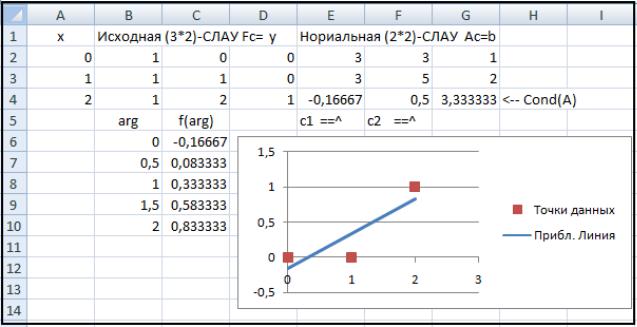
Можно изобразить результаты, полученные в предыдущем разделе, на точечной диаграмме (рис. 5.8), рассчитать точки на найденной прямой, добавить их к точечной диаграмме и соединить отрезками.
Рисунок 5.8.
Детали построения в Excel графика функции f(arg).
На отрезке [0;2] изменения аргумента (arg) рассчитаем несколько значений и, выделив занятый ими диапазон (B6:B10), присвоим ему имя «arg» (командами Формулы – Присвоить имя). Присвоим также соответственно имена «с1» и «с2» (с русскими буквами «с») ячейкам с вычисленными коэффициентами. В ячейку C6 запишем формулу «=c1+c2*arg» и, «протянув эту формулу» до ячейки C10, получим значения функции для построения графика. Выделим диапазон
B6:C10 и выполним команды Вставка-(диаграммы) Точечная - с
прямыми отрезками. Добавим к диаграмме «точки данных» (x и y) из диапазонов A2:A4 и D2:D4. Затем, выделив легенду «Точки данных» и вызвав (нажатием правой клавиши мыши) контекстное меню,
изменим тип диаграммы для ряда на точечная с маркерами.
Диаграмма даѐт картинку (см. на рис. 5.8), где прямая линия сглаживает точки, полученные в результате эксперимента и содер-
88

жащие случайные погрешности замеров. При этом сумма S квадратов отклонений точек данных от сглаживающей их линии будет минимальной, а всякое смещение этой линии от точек будет приводить к увеличению этой суммы. Рассмотрим это подробнее.
Сумма квадратов отклонений каждой из n точек данных от сгла-
живающей их линии |
f x |
равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) y |
|
|
|
|
|
|
2 ... |
2 . . |
2 |
2 |
T |
|
|||||||||||
S c |
f (x |
|
k |
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
k |
|
n |
|
|
|
|
|
|
||
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
T |
|
|
|
T |
F |
T |
|
|
|
|
|
T |
T |
T |
|
|
T |
T |
||||||||
(Fc y) |
(Fc y) c |
|
Fc 2cF |
y y y |
c Ac 2c |
b |
y y |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
cTAc 2cTb |
yTy , |
|
|
|
|
|
|
(5.2) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разность функции |
|
S c |
и еѐ значение |
S c* |
в точке найденного |
||||||||||||||||||||||
|
|
|
|
|
|
с2 * T можно преобразовать к выражению (5.3): |
|||||||||||||||||||||
решения с* с1*, |
|||||||||||||||||||||||||||
|
|
|
|
T |
|
|
|
|
|
T |
|
|
T |
|
T |
|
|
T |
|
T |
|
|
|||||
S(c) |
S(c ) c A c |
2c |
|
b y y (c |
A c 2c b |
y y) |
|
||||||||||||||||||||
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
* |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
||||
|
|
|
|
|
|
F(c c* ) T F (c c*) uT u u2 |
(5.3) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где u |
F (c |
c* ) . Последние выражения показывает, что эта разность |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
совпадает с век- |
|||||
неотрицательна и равна нулю только, когда вектор c |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тором |
решения |
c* . |
Рассматриваемая |
разность |
представляет |
собой |
|||||||||||||||||||||
квадратичную форму (при невырожденной матрице A) с точкой минимума
Для нашего конкретного случая сумма квадратов отклонений равна
S с , c |
3 |
1 |
f (x ) y |
k |
2 3 |
1 |
(c c x ) y |
k |
2 (c c 0 0)2 |
|
1 2 |
k |
k |
k |
1 2 k |
1 2 |
|
(c1 c2 1 0)2 (c1 c2 2 1)2 3c12 6c1c2 5c22 2c1 4c2 1
(c1 1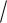 6)2 (c1 c2 1
6)2 (c1 c2 1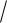 3)2 c1 2c2 5
3)2 c1 2c2 5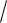 6 2 1
6 2 1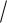 6
6
|
1 0 |
c 1 6 |
2 |
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|||
|
1 1 |
1 |
|
|
|
F c c* |
2 1 6 |
|||
|
|
|||||||||
|
|
|
c2 1 2 |
|
|
6 |
|
|
|
|
|
1 2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
89

То есть сумма принимает своѐ минимальное значение 1/6, когда век-
|
|
|
тор коэффициентов c совпадает с вектором решения c* , составляю- |
||
щие которого: |
с1* 1 6, |
с2* 1 2 . При всех иных значениях коэф- |
|
положительное первое слагаемое будет увеличивать |
|
фициентов c |
||
сумму квадратов отклонений S .
Выражение S с1, c2 задаѐт Z-координату выпуклого вниз эллиптического параболоида, вертикальная ось которого проходит через его нижнюю точку с координатами с1* 1 6, с2* 1 2, z 1 6 . В этой нижней точке касательные к параболоиду горизонтальны, а частные
производные по с1 и с2 , задающие тангенсы углов наклона соответствующих касательных, равны нулю. Такие равенства представляют необходимое условие экстремума
S |
2 3 c 6c |
|
2 0, |
S |
6c 2 5 c |
|
4 0 , |
|
2 |
|
2 |
||||
1 |
|
1 |
|
||||
c1 |
|
|
c2 |
|
|
||
и с учѐтом предыдущего анализа позволяют найти координаты точки минимума с1*, с2 * - искомые значения коэффициентов сглаживающей функции (линии) из системы
3c1 3c2 13c1 5c2 2
В общем случае, если взять производную по c (она берется также как для скалярного c ), то получаем уравнение
dS |
|
|
|
|
2 FTF c 2 |
FTy 0 , |
(5.4) |
dc |
|
|
|
которое равносильно нормальной системе уравнений для определе-
ния вектора c* :
|
|
|
. |
(5.5) |
|
FTF c FTy |
|||
Множители при коэффициентах в с1 1 с2 xk yk можно рассмат- |
||||
ривать как базисные функции f1(x) 1, |
f2 (x) x |
приближающей кри- |
||
вой f (x) c1 f1 (x) c2 f2 (x) , в общей задаче сглаживания данных.
90
