ЧМ В ИНЖЕНЕРНЫХ РАСЧЁТАХ(часть 1)_v1
.pdf
Метод Ньютона обладает только локальной сходимостью, т.е. областью его сходимостью является некоторая малая σ-окрестности корня и для гарантии сходимости необходимо вбирать хорошее начальное приближение, попадающее в эту σ-окрестность. Неудачный выбор начального приближения может дать расходящуюся последовательность итераций, например, представленную на рисунке
1.10.
y |
|
|
|
|
|
y=f(x) |
|
f(x1) |
|
|
|
|
|
|
x0=a |
b |
|
|
|
f |
f '(x0) |
x1 |
x2 |
x |
|
|
|||
Рисунок 1.10 – Метод Ньютона расходится при неправильном выборе x0 |
||||
Если вычисление первой производной функции на каждом шаге требует больших вычислительных затрат, можно использовать модифицированный метод Ньютона. Суть его заключается в том, что значение производной вычисляется один раз в начальной точке x(0) и это фиксированное значение подставляется в формулу (1.9):
xn 1 |
xn |
|
f (xn ) |
(1.9) |
|
f |
|
||||
|
|
|
(x0 ) |
|
|
Геометрическая интерпретация модифицированного метода Ньютона представлена на рисунке 1.11. В отличие от обычного метода касательных, в модифицированном методе предъявляется меньше требований к выбору начального приближения, а так же гарантировано отсутствие деления на ноль, если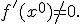 
. Однако, модифицированный метод имеет один существенный недостаток – резкое падение скорости сходимости.
21
y |
|
f(x0) |
|
|
|
|
f '(x0) |
f '(x0) |
|
|
|
0 |
|
|
|
x1 |
x |
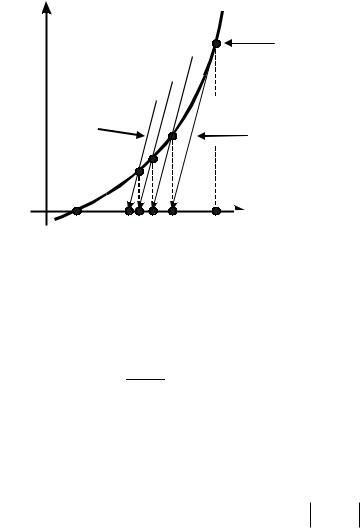
Рисунок 1.11 – Модифицированный метод Ньютона
Формула (1.9) совпадает с формулой метода простых итераций, если определить
= − ′((µ)) = − ( ),
где μ – значение абсциссы в некоторой точке отрезка локализации корня с максимальным значением первой производной функции f(x) на отрезке локализации корня.
Как уже показано, этот процесс сходится, если (x) 1 в интервале, в котором находится один корень уравнения f (x) 0, т.е.
´ = |
1 − < 1 |
Значение λ следует принимать:
= |
( ′ |
|
) |
(1.10) |
|
max |
′ |
|
|
||
где ( ′ ) – знак первой производной f(x) на интервале локализации корня [a,b];
max ( ′ ) – максимальное значение первой производной f(x) на интервале локализации корня [a,b].
1.4 Метод деления отрезка пополам
Метод обеспечивает нахождение единственного корня в интервале локализации х[a,b] с заданной точностью >0. Наличие корня
22
уравнения на интервале [a,b] (или нечетного числа корней) предполагает, что на границах интервала функция f(x) имеет разные знаки, т.е. f(a)·f(b)<0. Метод уточняет (сужает) границы интервала, где распо-
ложен корень. В дальнейшем интервал [a,b] будет обозначаться с указанием номера итерации - [a(0),b(0)].
В методе деления интервала пополам (методе бисекций) отрезок
локализации корня делится пополам (0) = (0)+ (0). Перемещая одну
2
из границ в точку x(0) уменьшаем отрезок локализации в два раза, т. е. заменяем начальный отрезок [a(0),b(0)] отрезком [a(1),b(1)] меньшей
длины. В методе бисекций в качестве [a(1),b(1)] берут тот из отрезков [a(0),x(0)] и [x(0),b(0)] на концах которого выполняется условие
f(a(1))·f(b(1))≤0. Этот отрезок содержит искомый корень. Если данное произведение равно нулю, то корнем уравнения является одна из гра-
ниц. Неограниченное продолжение итерационного процесса дает последовательность отрезков [a(0),b(0)], [a(1),b(1)], … , [a(n),b(n)], содержа-
щих искомый корень. Каждый из них, за исключением начального, получен делением пополам предыдущего отрезка.
При повторении процедуры деления, длина отрезка становится настолько малой (меньше заданной допустимой погрешности в определении корня), что можно приближенно за значение корня принять абсциссу любой точки отрезка [a(n),b(n)]. Считая, что (b a) является
абсолютной погрешностью, а (b a) / a - относительной погрешно-
стью вычислений корня уравнений, мы получаем возможность гарантированно выбирать значение корня с недостатком (принимая x a ) или с избытком (принимая x b). Обычно за корень уравнения принимают значение x(n).
23
y |
|
|
|
|
|
шаг 1 |
|
|
|
|
|
|
x(1) |
|
|
|
|
a(0) |
|
|
b |
(0) |
x |
|
|
|
|||
|
|
|
|
||
y |
|
x(2) |
шаг 2 |
|
|
|
|
|
|
||
a(1) |
|
|
b(1)=b(0) |
x |
|
|
|
|
|||
y |
x(3) |
|
шаг 3 |
|
|
a(2)=a(1) |
|
b(2) |
|
|
x |
|
|
|
|
||
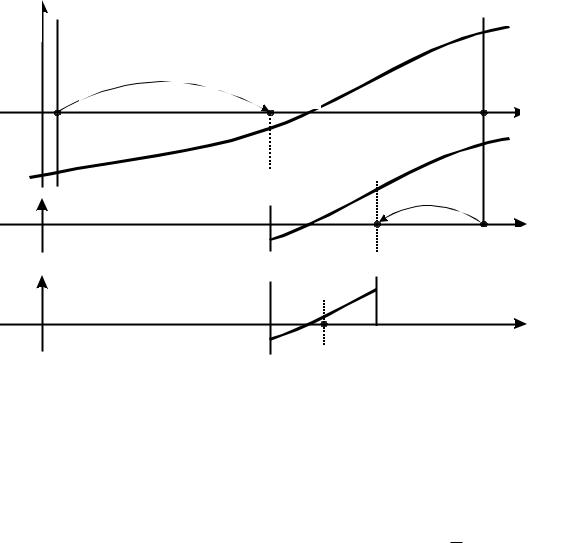
Рисунок 1.12 – Метод деления отрезка пополам |
|
||||
Пример 1.1
Используя графический способ отделения корней определить ин-
тервалы локализации корней уравнения sin x cos x 3x 0.
Данную задачу можно решить, используя электронную таблицу Excel и пакет Matlab. На рисунке 1.13 показан фрагмент электронной таблицы Excel (в режиме отображения функций) с графиком функции.
Для получения графика данной функции в пакете MATLAB, показанного на рисунке 1.14, необходимо выполнить следующую цепочку команд:
f=inline('sin(x)-cos(x)-x/3') figure;
fplot(f,[-3 3]); grid;
24
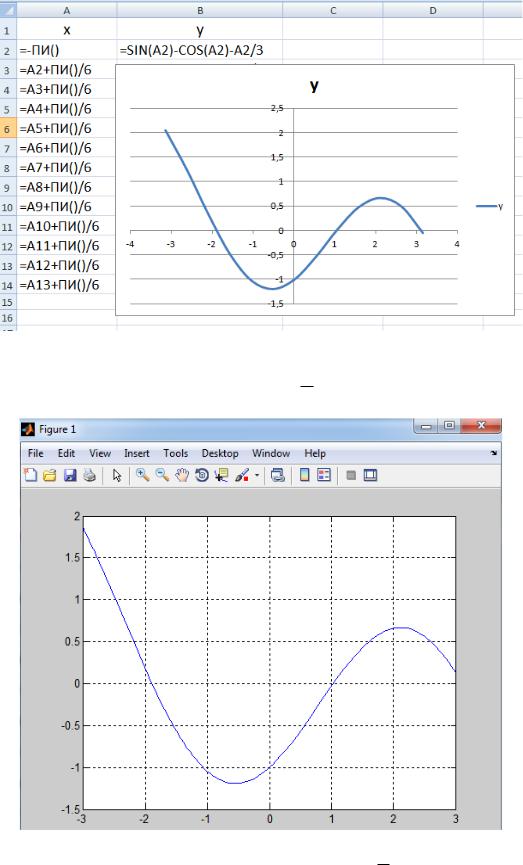
Рисунок 1.13 – Вид таблицы Excel с графиком функции sin x cos x 3x 0
Рисунок 1.14 – График функции sin x cos x 3x 0 построенный в пакете Matlab
25
Анализ графиков показывает три отрезка локализации корней:
[-2;-1], [0,5;1,5], [3;3,5].
Пример 1.2
Используя встроенную функцию fzero пакета MATLAB, найти корни уравнения f(x)=0. В квадратных скобках задаются левая и правая границы интервала, на котором расположен корень. Протокол работы в пакете Matlab представлен ниже.
»[x]=fzero(f,[-3 1]) x =
-1.8936
»[x]=fzero(f,[1 2]) x =
1.0308
Пример 1.3
Используя |
процедуру на VBA, найти два корня уравнения |
|
sin x cos x |
x |
0 с точностью =0.0001. |
|
||
3 |
|
|
Примечание. Вычисление третьего корня уравнения читателю предлагается выполнить самостоятельно.
Для реализации метода простых итераций необходимо преобразовать исходное уравнение к виду x (x) . Очевидно, что простейшее преобразование уравнения x=3·(sin(x)-cos(x)) (производная ′ = 3 · + ) не отвечает условию сходимости метода итераций. Поэтому, используем преобразование x x f (x), откуда
(x) x f (x) .
|
Значение |
λ |
выбираем |
из |
условия |
сходимости |
|||||||||||||
|
|
|
|
|
1 |
f |
|
|
1, |
т.е. |
|
|
|
|
|
1 |
|
решая нера- |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
(x) |
|
|
(x) |
|
|
(x) |
|
|
|1+ (cosx+sinx-3)|<1, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
венство получим
26
|
|
|
|
|
|
|
|
|
|
|
−2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
< <0 |
(1.11) |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
cos + − |
|
||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||
|
Для поиска корня в интервале [0,5;1,5], выбираем начальное при- |
|||||||||||||
ближение x = |
|
≈ 1,05 и подставляем его в формулу (1.11). Получа- |
||||||||||||
3 |
||||||||||||||
|
|
|
−2 |
|
|
|
|
|
|
|||||
ем |
|
|
|
< <0 или -1,94< <0. Для вычисления |
корня методом |
|||||||||
|
|
|
|
|
|
|
||||||||
1 |
|
3 |
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
+ |
|
|
− |
|
|
|
|
|
|
||
|
2 |
2 |
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|||||
итераций назначим значение =-1,3, которое лежит на отрезке [-1,94 ; 0].
Для корня, лежащего на отрезке [-2;-1], выберем начальное приближение x =-2, Так как производная f '(-2) отрицательная получим 0 < < −−1,662 или 0< <1,2. Для расчета можно назначить значение
= 0,9. Ниже приведен текст макроса на языке VBA вычисления корня уравнения лежащего на отрезке [0,5;1,5] методом простой итерации. В программе комментарием (оператором «REM») помечены строки, которые следует изменить для поиска корня на отрезке [-2; -1]. Оператором «Rem Ньютон» помечены строки, которые следует использовать, для вычисления корней методом Ньютона.
Sub main_Iter()
Dim a As Single, b As Single, delta As Single Dim x1 As Single, k1 As Integer
delta = 0.0001 ' заданная точность вычисления
x1 = 1.05 ' начальное приближения для вычисления ' корня в интервале [0,5; 1]
REM x1 = -2.0 ' начальное приближения для вычисления ' корня в интервале [-2; -1]
Call iter_1(delta, 100, x1, k1, 1)
Debug.Print "Ответ: Метод итераций x1="; x1, "k1="; k1
End Sub
Function fi(x) ' функция для вычисления итерационной формулы fi = x - 1.3*(Sin(x) - Cos(x) - x / 3) ' для корня на отрезке [0,5;1,5]
Rem fi = x + 0.9 *(Sin(x) - . . . для корня на отрезке [-2;-1] 27
Rem Ньютон fi = x - (Sin(x) - Cos(x) - x / 3)/(Cos(x)+Sin(x) 1/3)
End Function
Sub iter_1(Delta As Single, limit As Integer, _
x As Single, n As Integer, Optional KP As Integer = -1)
n = 0
Debug.Print " Метод итераций x= "; x
Do
x1 = fi(x)
If Abs(x - x1) < Delta Then Exit Sub
If KP>=0 Then Debug.Print "n="; n," x1="; x1, "Delta=";Abs(x-x1) x = x1
n = n + 1
If n >= limit Then
Debug.Print "Превышено число итераций"
Exit Sub End If
Loop End Sub
Результаты расчета макроса:
Метод итераций x= 1,05 |
|
|
||
n= 0 |
x1= 1,0241921981691 |
Delta= 2,58077541471815E-02 |
||
n= 1 |
x1= 1,03315175987991 |
Delta= 8,95954586776093E-03 |
||
n= 2 |
x1= 1,03000694509424 |
Delta= 3,14480070196588E-03 |
||
n= 3 |
x1= 1,03110673303375 |
Delta= 1,09984750518666E-03 |
||
n= 4 |
x1= 1,03072159268933 |
Delta= 3,851177446339E-04 |
||
n= 5 |
x1= 1,03085640517607 |
Delta= 1,34859956651301E-04 |
||
Метод итераций |
x1= |
1,030856 k1= |
6 |
|
28
Вычисление наименьшего корня методом деления отрезка пополам с относительной погрешностью, не превышающей Eps=0.0005, и с включѐнной вспомогательной печатью (KP=1):
Sub MainDOP() ' с хранением x, f в ячейках A1, B1 с именами "x", "f" ActiveWorkbook.Names.Add Name:="x", RefersToR1C1:="=Лист1!R1C1" ActiveWorkbook.Names.Add Name:="f", RefersToR1C1:="=Лист1!R1C2" Range("f") = "=SIN(x)-COS(x)-x/3" ' формулу в ячейку с именем «f» Debug.Print DOP("f", "x", -3, -1, Eps:=0.0005, KP:=1) , Range("x")
End Sub
Iter= 1 |
X=-2 |
Iter= 2 |
X=-1,5 |
Iter= 3 |
X=-1,75 |
Iter= 4 |
X=-1,875 |
Iter= 5 |
X=-1,9375 |
Iter= 6 |
X=-1,90625 |
Iter= 7 |
X=-1,890625 |
Iter= 8 |
X=-1,8984375 |
Iter= 9 |
X=-1,89453125 |
Iter= 10 |
X=-1,892578125 |
Iter= 11 |
X=-1,8935546875 |
True -1,8935546875
Интерфейс функции DOP (см. литературу [5]) представлен ниже:
Function DOP(Fch As String, Xch As String, a As Double, b As Double, _ Optional Eps As Double = 0.0001, Optional KP As Integer = -1, _
Optional Iter As Integer) As Boolean
' Fch, Xch - имена ячеек с функцией и аргументом,
'a, b - левая и правая границы отрезка, содержащего корень,
'Eps - относительная погрешность корня |X* - X|/max(|a|,|b|)<Eps,
'KP - код вспомогательной печати: KP<0 - нет вывода,
' |
KP>=0 - вывод в окно отладки, |
' |
Iter - число выполненных приближений (выходной параметр). |
29
Пример 1.4
Используя электронные таблицы Excel, найти корень уравнения sin x cos x 3x 0 с точностью =0.0001 методом простых итераций и методом касательных.
Решение данной задачи средствами Excel может быть выполнено:
с использованием циклических ссылок;
с помощью специальных средств Excel – «подбор параметра», либо «поиск решения»;
с использованием стандартных возможностей Excel.
Использование в Excel циклических ссылок для решения нелинейных уравнений является достаточно экзотической возможностью и, при желании, можно найти соответствующую статью в Интернет. Работа по подбору параметра и поиску решения описано в справке Excel, поэтому рассматривать этот способ не будем.
Вариант решения выше приведенного уравнения методом итераций представлен на рисунке 1.15. Значение параметра λ задается в ячейке D1 и используется в формуле ячейки В3 в абсолютной адресации. Диапазон ячеек A3:C3, с помощью маркера «Автозаполнения», затем «протягивается» вниз до тех пор, пока число с столбце «С» не станет меньше 0.0001.
Рисунок 1.15 – Фрагмент таблицы Excel реализующий метод простой итерации для решения уравнения sin x cos x 3x 0
На рисунках 1.16 и 1.17, в режиме отображения значений, представлены фрагменты таблицы Excel для нахождения двух корней
уравнения sin x cos x 3x 0 .
30