Lektsii_DM_Teoria_Grafov_2y_semestr

Дискретная математика: теория графов

Данный курс был прочитан для студентов второго курса факультета "К" групп К2-221, 222, 224, 281, 331 и 361 в весеннем семестре 2005/2006 учебного курса доц. Каф. Кибернетики Порешиным П.П.

Появление этого конспекта на сайте кафедры для студентов стало возможным благодаря инициативе студента группы К2-331 Шутяева Александра, который тщательно их записал с последующей обработкой текста в текстовом, графическом и формульном редакторах.

Основные объекты графов

метаграф

G V ,U

V - носитель метаграфа (конечное множество вершин).

V v1,v2 ,...,vp . U - сигнатура метаграфа (конечное множество связей между вершинами). U u1,u2 ,...,uq .

Граф, орграф и гиперграф отличаются друг от друга свойствами сигнатуры.

Для графа: U - множество ребер, связывающих две вершины.

Для гиперграфа (мограф – модельный граф): U - множество граней. u U u V . Грань – подмножество вершин мографа.

Примеры

Дискретная математика: теория графов

Если вершины vi и v j являются концевыми для некоторого ребра,

то говорят, что они смежны. Если два ребра имеют общую концевую вершину, то они также смежны. Если вершина является концевой для некоторого ребра, то говорят, что они инцидентны.

Все введенные ранее графы можно было бы разделить на три категории.

Дискретная математика: теория графов

взвешенные

метаграфы

f :V N; g :U K; N, K некоторые множества

Способы задания графов

1.Графический способ задания графов.

2.Матрица смежности (для вершин).

Для графа:

3.Матрица инциденций.

Для графа:

Дискретная математика: теория графов

Для орграфа:

G V , ,G V ,

:V B V - функция положительной полуокрестности.:V B V - функция отрицательной полуокрестности.

vi | v,vi U , vi | vi ,v U

Изоморфизм на графах

Изоморфизм обладает свойствами рефлексивности, симметричности, транзитивности, следовательно обладает свойством эквивалентности на множестве графов.

Примеры

Дискретная математика: теория графов

Матрица инциденций и матрица смежности задают граф с точностью до изоморфизма.

Количественная или качественная характеристика, неизменная для всех изоморфных между собой графов называется инвариантом графа. Поиск этих инвариантов – основная задача теории графов.

Элементы графов

подграфом графа G , если он является частичным графом подграфа графа G .

Степень вершины. Степень графа

Пусть G V , - некоторый граф.

Степенью вершины называется величина s v v - число дуг, инцидентных данной вершине. Степенью графа называется

величина s G max s vi . Минимальною степенью графа

vi V

называется величина G min s vi .

vi V

Дискретная математика: теория графов

Пример

Следствие Число вершин с нечетными степенями – четно.

Граф называется регулярным, если степени всех его вершин равны.

Дискретная математика: теория графов

Пример

Регулярный граф степени 2

Для орграфов:

s v v - полустепень исхода. s v v - полустепень входа.

Теорема

Для любого орграфа s vi s vi 2q .

vi V

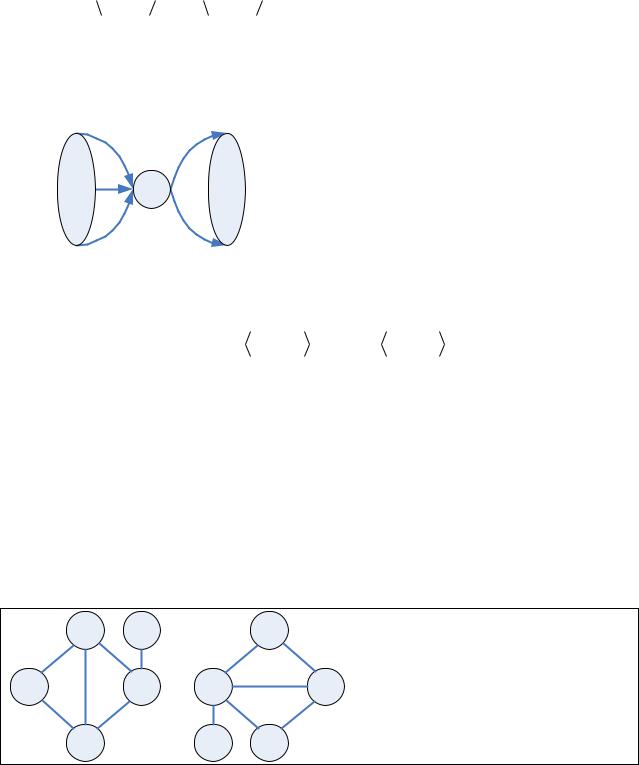
Пример

Распределение степеней вершин совпадает, но графы не изоморфны.

Типы графов

1.Граф и ограф.

2.pq -граф (граф, построенный на p вершинах и q ребрах).

Дискретная математика: теория графов

3.Полный граф на n вершинах Kn (все вершины смежны

между собой).

Пример ( K5 )

4.Тривиальный граф (граф, состоящий из одной вершины).

5.Пустой граф Pn (граф на n вершинах, не содержащий ни одного ребра U )

6.Двудольный граф (граф G V , называется двудольным,

если V Va Vb Va Vb и vi Va vi Vb иvj Vb vj Va ).

Примеры

7.Полный двудольный граф Km,n (двудольный граф, в котором

каждая вершина одной доли смежна с каждой вершиной другой доли).

Дискретная математика: теория графов

Пример ( K3,2 )

Операции на графах

Дискретная математика: теория графов

4. Операция сложения графов G Ga Gb

Ga Va ,Ua ,Gb Vb ,Ub ,G V ,U

(V Va Vb , KVa \Vb ,Vb \Va - полный двудольный граф, построенный на элементах Va и элементах Vb , которые не являются общими для этих двух графов. G Ga Gb KVa \Vb ,Vb \Va )