
Sapunov_Prikladnaya_teoriya_uprugosti_2008
.pdf
Для определения напряжений используем их комплексное представление в полярной системе координат:
σr + σθ = 2 [Φ(z)+ Φ(z)]= 4 Re Φ(z) ,
σθ −σr + 2 iτr θ = 2e2iθ [z Φ′(z)+Ψ(z)] .
Подставляя в приведенные соотношения комплексные функции Φ (z) и Ψ (z), будем иметь:
σr + σθ = 2 |
pa a2 |
− pb b2 |
, |
|
b2 |
− a2 |
|||
|
|
σθ −σr + 2iτrθ
σθ
= 2e2iθ |
( p |
a |
− p |
b |
) a2b2 |
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
b2 −a2 |
|
|
r2 |
2e2iθ |
||||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
( p |
a |
− p |
) a2b2 |
|
|||||
−σr + 2iτrθ |
= 2 |
|
|
b |
|
|
|
. |
||||||
r |
2 |
(b2 |
−a2 ) |
|||||||||||
|
|
|
|
|
|
|||||||||
Из второго соотношения следует, что τrθ = 0 и, соответственно,
|
( p |
a |
− p |
) a2b2 |
|
|
σθ −σr = 2 |
|
b |
|
. |
||
r2 |
(b2 |
−a2 ) |
||||
|
|
|||||
Определение напряжений σr и σθ приводит к известному результату:
σr =
σθ =
pa a2 − pb b2 b2 − a2
pa a2 − pb b2 b2 − a2
|
( pa − pb ) a2b2 |
− |
(b2 − a2 ) |
|
( pa − pb ) a2b2 |
+ |
(b2 − a2 ) |
|
1 |
, |
||
|
r 2 |
|||
|
|
|
|
|
|
|
1 |
. |
|
|
|
r 2 |
|
|
Решение рассматриваемой задачи в действительных переменных приведено в книге [1]. Там же проведен подробный анализ напряженного состояния с обсуждением его особенностей.
61
1.6.Решение граничных задач для полуплоскости
иплоскости с прямолинейными разрезами
1.6.1.Преобразование общих формул для полуплоскости
До сих пор рассматривали только такие области, граница которых состояла из замкнутых (конечных) контуров. Полуплоскость представляет собой случай, когда граница определяется разомкнутой линией, уходящей в бесконечность в обе стороны.
|
|
|
|
|
|
|
|
|
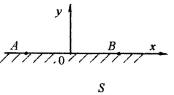
Пусть область, |
S |
занятая телом, |
|||
|
|
|
|
|
|
|
|
|
состоит из нижней |
полуплоскости |
||||
|
|
|
|
|
|
|
|
|
y < 0 |
(рис. 1.1), ограниченной осью |
||||
|
|
|
|
|
|
|
|
|
x . Будем считать, напряжения стре- |
|||||
|
|
|
|
|
|
|
|
|
мятся к нулю, когда |
переменная z |
||||
Рис. 1.1 |
|
|
|
|
|
удаляется в бесконечность по любому |
||||||||
пути, оставаясь внутри S . |
|
|
|
|
|
|
||||||||
Если бы контур области |
S не простирался в бесконечность, а |
|||||||||||||
был замкнутой кривой, то комплексные функции Φ(z) и Ψ(z) при |
||||||||||||||
больших значениях |
|
z |
|
|
имели бы вид (см. раздел 1.3.3): |
|||||||||
|
|
|||||||||||||
Φ(z)= |
γ1 |
+ |
γ2 |
|
+... , |
Ψ(z)= |
γ′1 |
+ |
γ′2 |
+ ... |
||||
|
|
|
z |
|
|
|
z2 |
|
|
z |
z2 |
|
||
Соответственно, для рассматриваемого случая можем записать:
|
|
Φ(z)= |
γ |
1 |
|
|
|
Φ′(z)= − |
γ |
|
1 |
|||||||||||||||
|
|
|
+ ο |
|
|
|
+ ο |
|
, |
|||||||||||||||||
|
z |
z2 |
|
|||||||||||||||||||||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|||||
|
|
|
|
|
|
|
(z)= |
γ′ |
|
|
|
1 |
, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Ψ |
|
+ ο |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|||||
где γ и γ′ |
|
− постоянные. Напомним, что символом ο(1/ z) обозна- |
||||||||||||||||||||||||
чается такая величина, что |
|
ο(1/ z) |
|
< ε / |
|
z |
|
, где ε |
зависит только |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
от модуля |
|
z |
|
и стремится к нулю при |
|
|
z |
|
|
→ ∞. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
62

Интегрируя комплексные функции Φ(z) и Ψ(z), получим:
ϕ(z)= γln z + ο (1)+ const |
, ψ(z)= γ′ln z + ο (1)+ const |
, |
||||||||||||
где символ ο(1) определяет такую величину, что |
|
ο(1) |
|
|
|
< ε , где ε |
||||||||
|
|
|||||||||||||
зависит только от модуля |
|
z |
|
|
и стремится к нулю при |
|
|
|
z |
|
|
→ ∞. В |
||
|
|
|
|
|
||||||||||
представленных соотношениях следует выбрать одну ветвь многозначной функции ln z , например ln z +iθ , где θ изменяется от
θ = −π до θ = 0 .
Будем считать, что главный вектор внешних сил, приложенных к отрезку AB оси x , стремится к определенному пределу, когда концы отрезка уходят в бесконечность ( A − влево, а B − вправо)1.
При положительном направлении обхода контура, когда область S , занятая телом, остается слева, компоненты главного вектора нагрузки, приложенной к участку AB контура, определяются соотношениями (см. раздел 1.2.4):
|
∂U |
|
∂U B |
∂U |
|
∂U |
|
|
|
|
|
|
||
|
+i |
|
′ |
(z)+ ψ(z) . |
||||||||||
X +iY = −i |
|
+i |
|
|
, |
|
|
|||||||
∂x |
|
∂x |
∂y |
= ϕ(z)+ zϕ |
||||||||||
|
|
∂y A |
|
|
|
|
|
|
|
|||||
Соответственно, если X ′ , Y′ − компоненты главного вектора нагрузки, приложенной к отрезку AB границы полуплоскости, будем иметь:
|
∂U |
+ i |
∂U |
B |
|
|
|
|
|
|
|
||||||||
X ′+iY ′ = i |
|
= i [ϕ(z)+ zϕ′(z)+ ψ(z)]BA , |
|||||||
|
∂x |
|
∂y |
A |
|||||
поскольку направление обхода от A к B − отрицательное.
Если точки A и B находятся по разные стороны от начала координат и достаточно далеко друг от друга, то использование ком-
1Принятое условие всегда выполняется, если нагружен конечный участок границы.
63

плексных функций ϕ(z) и ψ(z) в полученном виде приводит к соотношению:
|
′ |
|
′ |
|
|
r′′ |
|
|
|
|
|
r′′ |
|
|
|
|
|
|
|
|
|
′ |
|
′ |
|||||||||
X |
+iY |
= i |
γln |
|
|
ln |
|
|
||||||||
|
|
r′ |
+ γπi + γ |
r′ |
− γ πi +ε , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где r′ и r′′ − расстояния точек |
A и B |
от начала координат; ε − |
||||||||||||||
малая величина, стремящаяся к нулю при возрастании r′ и r′′ . Из полученного соотношения следует, что компоненты главного вектора X ′ , Y′ будут оставаться ограниченными при сколь угодно больших r′ и r′′ , если выполняется условие:
γ+ γ′ = 0 .
Втаком случае компоненты главного вектора X , Y нагрузки, приложенной ко всей границе полуплоскости (ко всей оси x ), будут определяться соотношением:
X +iY = −π(γ − γ′) ,
откуда можно получить:
|
X +iY |
|
|
′ |
|
X −iY |
|
|
γ = − 2π , |
γ |
= − 2π . |
||||||
|
||||||||
С учетом полученных значений постоянных γ и γ′ комплексные функции будут иметь вид:
Φ(z)= − |
X +iY |
|
1 |
, |
Ψ(z)= |
X −iY |
|
1 |
; |
||
|
+ ο |
|
|
|
+ ο |
|
|
||||
2πz |
|
2πz |
|
||||||||
|
z |
|
|
|
z |
|
|
||||
ϕ(z)= − X 2+πiY ln z + ο (1)+ const ,
ψ(z)= X 2−πiY ln z + ο (1)+ const .
64
Используя полученные соотношения для комплексных функций, напряженное и деформированное состояния можем определить по известным формулам (см. разделы 1.2.2 и 1.2.3):
2μ(u +iv) = κϕ(z)− zϕ′(z)−ψ(z) ;
σx +σy = 2 [Φ(z)+Φ(z)]= 4 ReΦ(z) , σy −σx + 2iτxy = 2 [z Φ′(z)+ Ψ(z)] .
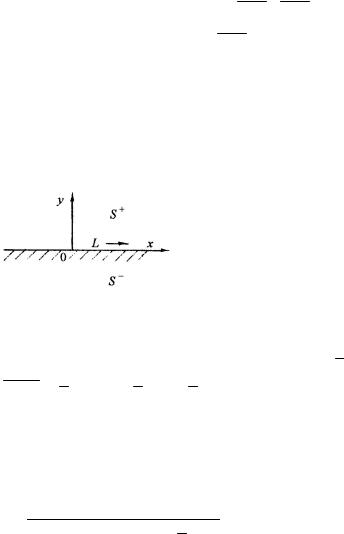
Принимая теперь для области, занятой телом (нижней полуплоскости Im(z)≤ 0 ) обозначение S − , а для оси x − L (рис. 1.2), распространим определение комплексных функций на верхнюю полуплоскость S + .
|
|
|
Условимся сначала о некоторых |
||
|
представлениях. Если функция F (z) |
||||
|
определена в области S − , то функция |
||||
|
|
|
(z)= |
|
|
|
|
F |
F (z )1 определена в области |
||
Рис. 1.2 |
S + (данное утверждение проверяется |
||||
с привлечением соотношений Коши − Римана). Соответственно, если существует граничное значение F − (t) в точке t действительной оси x , то существует и граничное значение F + (t), причем
F −(t) = F + (t) или F −(t) = F + (t).
Построим аналитическое продолжение функции Φ(z) в верх-
нюю полуплоскость S + так, чтобы ее значения в этой полуплоскости аналитически продолжили значения, принимаемые в нижней полуплоскости через незагруженные участки границы (если таковые имеются).
1Если Φ(z)= u (x, y)+iv (x, y), то Φ(z)= u1 (x, y)+iv1 (x, y), где u1 (x, y)=u (x, − y), v1 (x, y)= −v (x, − y).
65

На незагруженном участке границы имеем, что σy = τxy = 0 . Поскольку
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
(z)+Ψ(z) , |
||||||||||||||
|
σy −iτxy = Φ(z)+Φ(z)+ z Φ |
|||||||||||||||||||||||||||||||
граничное условие принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
|
|
|
σy −iτxy |
y=0 |
= Φ |
(t)+ Φ |
(t)+t Φ |
′ |
(t)+Ψ |
(t)= 0 , |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда непосредственно следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Φ− (t)= − |
|
− (t)−t |
Φ′−(t)− |
|
−(t) . |
|
|
|
|
|
||||||||||||||||||||
|
|
Ψ |
|
|
|
|
|
|||||||||||||||||||||||||
Φ |
|
|
|
|
|
|||||||||||||||||||||||||||
Можно утверждать, что функция Φ(z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
′ |
|
|||||||||||||||||||||||
= −Φ(z)− z Φ (z)−Ψ(z) |
||||||||||||||||||||||||||||||||
голоморфна в области S − . Голоморфной в этой области является и |
||||||||||||||||||||||||||||||||
функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Φ(z)= −Φ(z )− z Φ′(z )−Ψ(z ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z)−Ψ(z) |
|
будет голоморфной в |
|||||||||||||||||
Функция Φ(z)= −Φ(z)− z Φ |
|
|||||||||||||||||||||||||||||||
области S + . Действительно, Φ(z)= −Φ(z )− z Φ′(z )−Ψ(z )
Φ(z )= − Φ(z )− z Φ′(z ) −Ψ(z ) Φ(z)= −Φ(z)− z Φ′(z)−Ψ(z).
Соответственно, на границе Im(z)= 0 (на границе L , при z → t со стороны S + ) имеем:
Φ+ (t)= −Φ + (t)−t Φ′+(t)− Ψ + (t) .
Сопоставление полученных соотношений для Φ− (t) и Φ+ (t)
с учетом равенства |
|
|
|
−(t) = |
|
|
+ (t), принимающего здесь форму |
|||||
|
F |
F |
||||||||||
|
|
− (t ) = |
|
+ (t) и |
|
−(t ) = |
|
+ (t), позволяет получить: |
||||
|
Φ |
Φ |
Ψ |
Ψ |
||||||||
|
|
|
|
|
|
|
|
Φ− (t) = Φ+ (t) . |
||||
66

Следовательно, функция Φ(z)= −Φ(z)− z Φ′(z)−Ψ(z), опреде-
ленная в верхней полуплоскости S + , является аналитическим продолжением через ненагруженные участки границы L голоморфной
в нижней полуплоскости S − функции Φ(z). Иными словами, функция Φ(z)= −Φ(z)− z Φ′(z)−Ψ(z) представляет кусочно-голо-
морфную функцию во всей плоскости, разрезанной вдоль нагруженных участков границы L .
Аналитическое продолжение комплексной функции Ψ(z) на
верхнюю полуплоскость S + легко получить, используя соответствующее соотношение для функции Φ(z). Действительно, Φ(z)=
|
|
|
|
|
|
|
z → z |
|
|
′ |
(z) −Ψ(z), |
||
|
|
|
′ |
|
|
|
|||||||
|
|
|
(z)−Ψ(z) |
|
|||||||||
= −Φ(z)− z Φ |
→ Φ(z)= −Φ(z) − z Φ |
||||||||||||
откуда имеем: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
′ |
(z) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Ψ(z)= −Φ(z)−Φ(z)− z Φ |
|
||||||||
Полученное соотношение позволяет упростить формулы, описывающие напряженное состояние, записав их через одну функцию Φ(z), определенную как в верхней, так и в нижней полуплоскости:
σx +σy = 2 [Φ(z)+Φ(z)] , (1.8) σy −σx +2iτxy = 2 [(z − z)Φ′(z)−Φ(z)− Φ(z)] .
Переходя во втором уравнении к сопряженным значениям и складывая его с первым, можно получить еще одно соотношение для напряжений, удобное для использования в некоторых случаях:
|
|
|
|
(1.8, а) |
|
′ |
(z) . |
||
σy −iτxy =Φ(z)−Φ(z)+(z− z)Φ |
|
|||
Для аналогичных преобразований формулы, определяющей комплексное представление перемещений, необходимо получить
67
аналитическое продолжение на верхнюю полуплоскость S + функций ϕ(z) и ψ(z). С этой целью продолжим голоморфную в облас-
ти S − функцию ϕ(z) в область S + так, чтобы в этой области ϕ′(z)= Φ(z), где функция Φ(z) уже определена соотношением:
|
|
|
|
|
|
|
′ |
(z)+ψ(z)] |
′ |
|
|
|
|
′ |
|
|
|
|
|||
|
|
|
(z)−Ψ(z) |
. |
||||||
Φ(z)= −Φ(z)− z Φ |
Φ(z)= −[zϕ |
|
||||||||
Представленные соотношения позволяют определить производную функции ϕ(z) и саму функцию:
′ |
′ |
(z)+ ψ(z)] |
′ |
|
|
|
′ |
|
|
|
|
|
|||||||
ϕ |
(z)= −[zϕ |
|
ϕ(z)= −zϕ (z)−ψ(z) +const . |
||||||
Аналитическое продолжение комплексной функции ψ(z) на
верхнюю полуплоскость S + легко получить аналогично тому, как это было сделано для функции Ψ(z). Будем иметь:
ψ(z)= −ϕ(z) − zϕ′(z)+const .
Теперь и перемещения могут быть представлены через одну функцию ϕ(z), определенную как в верхней, так и в нижней полуплоскости:
2μ(u +iv) = κϕ(z)+ ϕ(z )−(z − z) |
|
|
(1.9) |
ϕ′(z)+ const . |
|||
Отметим, что постоянная, входящая в полученную формулу, определяет жесткое поступательное перемещение всего тела и, соответственно, может быть принята равной нулю.
1.6.2. Решение первой основной граничной задачи для полуплоскости
Пусть тело занимает нижнюю полуплоскость (см. рис. 1.2). Будем считать, что заданы внешние нагрузки в форме давления P (t)
68

и сдвигающих усилий T (t), приложенных ко всей границе L , причем P (∞)= T (∞)= 0 (нагрузки исчезают при t → ∞). Напомним, что составляющая P (t) представляет собой проекцию внешней нагрузки на внешнюю нормаль n , а T (t) − проекция той же на-
грузки на касательную t к границе, направленную влево, если смотреть вдоль n (по положительному направлению обхода контура).
Согласно соотношению (1.8, а) граничное условие в поставленной задаче принимает вид:
Φ+(t)−Φ−(t)= P(t)+iT (t) ,
поскольку при z , стремящемся к t из нижней полуплоскости, Φ(z) стремится к Φ−(t), Φ(z) стремится к Φ+(t), а (z− z)Φ′(z)=
= 2i yΦ′(z) стремится к нулю. Тем самым, задача сведена к отысканию кусочно-голоморфной функции Φ(z) по заданному скачку
Φ+(t) −Φ−(t)= f (t) на L . Решение этой задачи известно:
Φ(z)= |
1 |
∫ |
f (t) |
dt = |
1 |
∫ |
P (t)+ iT (t) |
dt . |
||
2πi |
t − z |
|
2πi |
t − z |
|
|||||
|
|
L |
|
|
|
|
L |
|
|
|
Таким образом, первая основная граничная задача для полуплоскости решена, поскольку функция Φ(z) определяет и компо-
ненты тензора напряжений, и перемещения по уже известным формулам.
1.6.3. Решение первой основной граничной задачи для плоскости с прямолинейными разрезами
Пусть область всю плоскость, ( k =1, 2, ..., n ) оси через L .
S′ , занятая упругим телом, представляет собой разрезанную вдоль n отрезков Lk = akbk x ; совокупность всех этих отрезков обозначим
69

В отличие от ранее рассматриваемой задачи (см. раздел 1.6.1), будем предполагать, что напряжения ограничены на бесконечности. В этом случае комплексные функции ϕ(z) и ψ(z) принимают
вид (см. раздел 1.3.3):
ϕ(z) = − |
X +iY |
ln z +Γz +ϕ |
0 |
(z) |
, |
||||
|
|
||||||||
|
|
2π(1+ κ) |
|
|
|
||||
|
|
|
|
|
|
||||
ψ(z) = |
κ(X |
−iY ) |
|
′ |
|
|
, |
||
|
|
|
|
|
|
|
|||
2π(1+ κ) |
ln z +Γ z +ψ0(z) |
||||||||
|
|
|
|
|
|
||||
где Γ = B +iC , Γ′ = B′+iC′ |
− комплексные постоянные; ϕ0 (z) и |
||||||||
ψ0 (z) − функции, представляемые при достаточно больших значе-
ниях |
z |
|
разложениями вида |
|
|
|
|
|
|
|||||
|
ϕ0 |
(z)= a0 |
+ |
a1 |
+ |
a 2 |
+ ... , |
ψ0 (z)= a′0 |
+ |
a1′ |
+ |
a′2 |
+ ... |
|
|
z |
z2 |
z |
z2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Соответственно, комплексные функции Φ(z) и Ψ(z) при достаточно больших значениях z можем записать в форме:
Φ(z)= − |
X +iY |
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
+Γ +Ο |
|
|
, |
||
2π(1+ κ) z |
|
|||||||||
|
|
z2 |
|
|
||||||
Ψ(z) = |
κ(X −iY ) |
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
+Γ′+Ο |
|
|
. |
|
2π(1+ κ) z |
|
|
||||||||
|
z2 |
|
|
|||||||
Действительные постоянные B , B′ и C′ , входящие в соотношения для функций Φ(z) и Ψ(z) посредством комплексных по-
стоянных Γ и Γ′, имеют простой физический смысл.
B = (N1 + N2 )/ 4 ,
Γ′ = B′+iC′ = −(N1 − N2 )e −2iα / 2 ,
70
