Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Ekzamen_bilety.doc

Скачиваний:

Добавлен:

04.06.2015

Размер:

4.05 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1

Модель однофакторного дисперсионного анализа. Разложение суммы квадратов.

Разложение суммы квадратов в однофакторном ДА.

В п.4.2 рассматривался вопрос включения в регрессию качественных переменных. В случае, когда регрессорами являются только качественные переменные, общепринятым методом исследования выступает дисперсионный анализ (ДА).

В зависимости от числа регрессоров, называемых в ДА факторами, говорят об одно-, двух-, многофакторном ДА. Сами факторы полагаются неслучайными (модель с постоянными эффектами) либо случайными (модель со случайными эффектами). В модели с постоянными эффектами речь идет в основном о сравнении средних значений количественной переменной при различных значенииях факторов, тогда как в моделях со случайными эффектами интересует доля изменчивости, вносимая отдельными факторами. Ниже рассматривается первая модель, для которой ДА часто называют одно-, двух-, многофакторной классификацией.

Однофакторный дисперсионный анализ

Имеется количественная переменная у, определяемая качественной переменной, иначе фактором, принимающимрдискретных значений (уровней). Так, фактором может быть «поставщик», уровнями – определенные фирмы-поставщики, переменнойу– срок службы поставляемого товара. В качестве исходных данных выступает выборка, содержащая ряд наблюдений на каждом из уровней (по нескольку экземпляров определенного товара от каждого поставщика). Необходимо ответить на вопрос – различаются ли по сроку службы объекты от разных поставщиков.

Модель однофакторного анализа: , (5.1)

где – наблюденные значения,N_i –объем выборки для i-го уровня фактора. Параметрmобозначает некоторую точку отсчета,a_i– эффект (вклад)i-го уровня фактора,u_ij– независимые, нормально распределенные случайные возмущения, удовлетворяющие предпосылке 5 классической регрессии.

Модель (5.1) не позволяет однозначно оценить параметры, поскольку можно добавить к mи вычесть изa_iпроизвольную константу. Неоднозначность снимается условием репараметризацииN₁a₁+N₂a₂+…+N_pa_p=0. (5.2)

Оценивание параметров производится по методу наименьших квадратов (МНК). Для минимизации остаточной суммы квадратовнайдем первые производные:

;

Обозначим . Из выражений для производных с учетом (5.2) получаем:

. (5.3)

(Точка на месте индекса означает усреднение по этому индексу.)

Результаты измерений принято представлять в виде табл.11.

Таблица 11

Уровни фактора	Наблюдения	Сумма внутри уровня	Среднее по уровню
1			₁_

р			_p_.

Модель и основная теорема факторного анализа

Модель и основная теорема факторного анализа.

В отличие от метода главных компонент факторный анализ заранее объясняет ковариационную (либо корреляционную) матрицу исходных переменных (признаков) наличием небольшого числа гипотетических факторов, присутствующих в исходных переменных. На языке корреляций это можно интерпретировать следующим образом. Вначале анализируется на значимость исходная корреляционная матрица, т.е. отличается ли корреляционная матрица значимо от единичной. Если это имеет место, то возникает вопрос: существует ли скрытая, иначе латентная, случайная величина такая, что попарные корреляции между исходными переменными станут равными нулю, если влияниеуже учтено? Пусть после этого элементы корреляционной матрицы все еще отличны от нуля. Тогда пытаются найти две случайные величиныитакие, что корреляции между исходными переменными станут нулевыми, если влияниеиуже учтено, и так далее.

Тем самым корреляция между nнаблюдаемыми признакамисвязывается с тем фактом, что эти признаки зависят от меньшего числа других, непосредственно неизмеряемых переменных, которые принято называть общими факторами.

Модель факторного анализаВ общем случае нельзя гарантировать, что каждый из исходных признаков зависит лишь отmобщих факторов, одних и тех же для всех признаков. Поэтому в факторном анализе постулируется, что наблюдаемый признакx_i(i=1,2,…,n)зависит также и от некоторой характерной для себя остаточной (шумовой) случайной компоненты. Итак, линейная модель факторного анализа имеет вид:

, (11.1)

где коэффициенты называютнагрузкойj-го общего фактора наi-й исходный признак, а матрицу,i=1,2,…,n;j=1,2,..,m–факторным отображением, либо матрицей факторных нагрузок.

Предпосылки факторного анализа. Предполагают, что исходные признаки подчиняются многомерному нормальному распределению; общие факторы некоррелированы, а их дисперсии равны единице, следовательно, корреляционная матрицаобщих факторов является единичной, т.е.; характерные (остаточные) факторы– нормально распределенные случайные величины, не зависимые друг от друга и от общих факторов. Это означает, что корреляционная матрицаVхарактерных факторов имеет диагональный вид. Все случайные величины имеют нулевое математическое ожидание.

Факторные нагрузки и дисперсиихарактерных факторов являются неизвестными параметрами, подлежащими оценке.

Вводя векторные обозначения: ,

перепишем модель факторного анализа (11.1) в виде: . (11.1а)

Ковариационная матрица исходных признаков с учетом их центрированности по определению естьC_x = M[xx^/],

где математическое ожидание берется по множеству реализаций вектора x.

Подставим в выражение (11.1а):C_x = M[(Ay+u)(Ay+u)′] = M[(Ay+u)(y′A′+u′)].

Раскрывая скобки в последнем выражении и учитывая, что общие и характерные факторы некоррелированы и, следовательно, M[u′y]=0, M[yu′]=0, а также неслучайный характер матрицыA, что позволяет выноситьАза знакМ, получаемC_x= AM[yy′]A′+M[uu′].

M[yy′] есть не что иное, как ковариационная матрицаобщих факторов, аM[uu′] ковариационная матрицаVхарактерных факторов. Таким образом,. (11.2)

Согласно предпосылкам факторного анализа есть единичная диагональная матрица. Следовательно,

. (11.2а)

Соотношение (11.2) либо (11.2а) иногда называют фундаментальной теоремой факторного анализа. Она утверждает, что ковариационная матрица исходных признаков может быть воспроизведена с помощью матрицы факторных нагрузок и дисперсионной матрицы характерных факторов.

На практике обычно используют не ковариационную , а корреляционную матрицуR исходных признаков. Переход от ковариационной к корреляционной матрице означает, что исходные центрированные переменные подвергаются нормированию делением значений каждого признака на среднее квадратическое отклонение этого признака. Такое преобразование позволяет избежать влияния масштаба измерения на результаты анализа. Преобразованные признаки будут иметь, очевидно, единичную дисперсию, их ковариационная матрица совпадает с корреляционной, а соотношение (11.2) примет вид:, (11.3)

где ВиWимеют тот же смысл, чтоAиV, но для нормированных признаков.

Для диагональных элементов матрицы Rвыполняется соотношение:,

где – диагональные элементы матрицыW.

Сумму квадратов нагрузок общих факторов называют общностью:. (11.4)

Общность указывает ту долю единичной дисперсии исходного признака, которую можно приписать общим факторам. Часть единичной дисперсии, которая не связана с общими факторами, называют характерностью:. (11.5)

Характерность иногда разбивают на две составляющих, одна из которых, , называется специфичностью, а другая,, является дисперсией, обусловленной ошибкой, т.е..

Факторное изображение допускает геометрическую интерпретацию. Согласно (11.1) точка в n-мерном пространстве исходных признаков представляется в виде линейной комбинацииm+nкоординат точки в пространстве общих и характерных факторов, называемом также полным факторным пространством. Так как нагрузки общих факторов однозначно определяют дисперсии характерных факторов, то достаточно представлять признаки вm-мерном ортогональном пространстве общих факторов. Поскольку пространство общих факторов имеет размерность наnменьшую размерности полного факторного пространства, в факторном анализе используют обычно пространство общих факторов. Строки матрицыВфакторных нагрузок рассматривают как точки в пространстве общих факторов. Координатыi-й точки есть. Соединяя эти точки с началом координат, получаемnвекторов-признаков. Длина вектора, отвечающегоi-му признаку, равняется, как видно из (11.4), корню квадратному из общности.

На рис. 13 в качестве примера приведена графическая иллюстрация факторного отображения.

Рис.13. Графическая иллюстрация факторного отображения

Числа 1,2,…,5 около точек соответствуют номерам строк матрицы В, иначе номерам исходных признаков.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2

Проверка гипотез в однофакторном ДА.

Проверка гипотез в однофакторном ДА.

В ДА основной интерес представляет не столько сами оценки, сколько их сравнение и, в первую очередь, проверка гипотезы Н₀:а₁=а₂=…=а_р=0, означающей одинаковость, неразличимость, воздействий всехруровней. Со статистической точки зрения задачу ДА можно сформулировать так: для каждой изргенеральных совокупностей получено по выборке объемомN_iи необходимо сопоставитьрзначений выборочных средних.

ДА базируется на разложении общей суммы квадратов S₀отклонений наблюденийот общего среднегона составляющие, связанные с рассеянием между уровнямиS_муи рассеянием внутри отдельных уровнейS_ву:

,S_му=, S_ву=.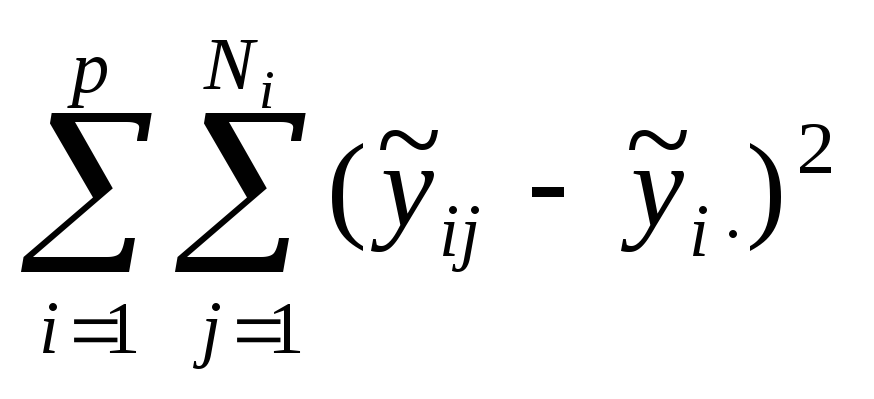

Подобное разложение получается следующим образом. Обе части тождества

возводят в квадрат и суммируют по iиj:

(5.4)

Последнее слагаемое в правой части формулы (5.4) обращается в нуль в силу выполнения следующей очевидной цепочки равенств:

Соотношение (5.4) приобретает вид S₀=S_му+S_ву. СуммыS₀,S_му,S_вуимеютN-1,p-1,N-pстепеней свободы соответственно. Если имеет место проверяемая гипотезаН₀, то каждое из отношений:

может служить оценкой дисперсии ²случайных возмущений. В силу нормальности возмущений отношениеимеетF-распределение. Полученные значения представляют в виде табл.12.

Таблица 12

Источник изменчивости	Сумма квадратов	ЧСС	Среднее	F-отношение
Между уровнями	S_му	p-1		F_р=
Внутри уровней	S_ву	N-p
	S₀	N-1

Гипотеза Н₀:а₁=а₂=…=а_р=0 отвергается при выбранном уровне надежности (обычно, 95%), еслиF_р>F_Т, гдеF_Т– табличное значениеF-распределения при ЧСС числителя и знаменателяp-1 иN-p соответственно. ПриF_рF_Тделается вывод, что результаты наблюдений не противоречат гипотезеН₀.

Основные этапы факторного анализа.

Основные этапы факторного анализа

Вычислительный аспект факторного анализа связан с определением факторного отображения В, дисперсий характерных факторов и оценкой значений общих факторов. Оценка этих параметров производится на основании экспериментальных данных, полученных в ходе наблюдений надNобъектами (индивидами). Результаты наблюдений представляются в виде матрицы исходных данных, аналогичной (11.1). По матрицеХвычисляется корреляционная матрицаR. Затем начинаются этапы собственно факторного анализа. Первый этап – оценка общностей. Если общности оценены, то по формуле (11.5) можно оценить характерности, а следовательно, и матрицуW, которая является диагональной согласно предпосылкам факторного анализа. Заменяя диагональные элементы матрицыRна оценки общностей, получают матрицу, которая является информационной основой второго этапа выделения факторов. На этом этапе решают тем или иным способом матричное уравнение, получая в итоге ортогональную матрицуA. Возможно большое число матрицA, которые одинаково хорошо будут воспроизводить матрицу. Из них должна быть выбрана одна, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, из-за большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.

Выделение факторов. Выделение факторов предполагает установление числа и направления осей координат, соответствующих общим факторам, необходимым для отображения корреляции исходных переменных. С алгебраической точки зрения проблема факторов означает определение ранга матрицыАи оценивание ее элементов. Для решения задачи выделения факторов разработано достаточно много методов, однако основными в настоящее время следует признать два: метод главных факторов, наиболее широко употребляемый на практике, и метод максимального правдоподобия, имеющий прочный математико-статистический фундамент.

Метод главных факторов.Как следует из фундаментальной теоремы факторного анализа (11.3),. Приравняем вначалеWнулевой матрице. Получим матричное уравнение. (11.6)

Матричное уравнение (11.6) имеет множество решений: любое ортогональное преобразование Т, переводящее матрицуВвG, т.е.G = ВТ, удовлетворяет (11.6). Действительно, в силу ортогональностиТимеет местои, значит,. Подставляя выражение дляВв (11.6), получаем, посколькуT′T=I.

Как известно из линейной алгебры, ортогональное преобразование системы координат означает поворот системы как целого на некоторый угол вокруг начала координат. Выделяя некоторое предпочтительное направление и фиксируя тем самым угол поворота системы координат, можно обойти проблему неоднозначности решения системы (11.6).

Вернемся на время к методу главных компонент. Выбор осей координат здесь подчинен определенному требованию: каждая следующая ось ориентирована по направлению максимальной дисперсии в пространстве, ортогональном предыдущим главным компонентам. Матрица весовых коэффициентов Апри этом составлена из собственных векторов ковариационной (корреляционнойR) матрицы. Следовательно,

, (11.7)

где – диагональная матрицaс элементами, равными собственным значениям корреляционной матрицы. Умножая (11.7) насправа и учитывая ортогональностьA, а значит, получаем:.

Обозначим через матрицу порядка, элементы которой равняются квадратному корню из соответствующих элементов матрицы Λ. Перейдем отAк. Выражение дляRпримет вид:

. (11.8)

Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы Вможно взять матрицу.

Таким образом, матрица факторных нагрузок получается из матрицы, составленной из собственных векторов корреляционной матрицы исходных признаков, с последующим умножением элементов собственного вектора, отвечающего i-му собственному значениюна.

Матрицы BиQ имеют разный порядок:уВиуQ, поэтому правильнее говорить, что оценкой будут первыеmстолбцов матрицыQ.

Посчитав матрицу Wравной нулю, мы для оценки матрицыBвоспользовались моделью главных компонент. Строго говоря, под методом главных факторов понимают способ расчета, принятый в методе главных компонент, но примененный к матрице(оценка общностей рассматривается ниже).

0ценка числа общих факторов. Общепризнанного метода определения числаmобщих факторов, подлежащих выделению, не существует. Однако разработан ряд критериев, с помощью которых можно сделать достаточно обоснованное заключение.

Широкое применение получил сравнительно простой критерий собственных значений: выделять только те факторы, которые соответствуют собственным значениям, большим единицы.

Рассмотрим матрицу .Справедлива следующая цепочка равенств:.

Полученное соотношение показывает, что сумма квадратов нагрузок i-го общего фактора на исходные признаки равняетсяi-му собственному значению. Нохарактеризует вкладi-го общего фактора в полную дисперсию (напомним, что полная дисперсия равняется следу корреляционной матрицыRи). Поэтому факторы, вклады которых меньше единицы, имеют долю дисперсии, меньшую единичной дисперсии исходных признаков, и их нецелесообразно включать в число общих факторов.

Считается также, что вклад общих факторов в суммарную общность должен составлять около 90%, а число общих факторов не должно превышать половины числа исходных признаков, т.е. m<n/2, а более точно,.

К проблеме оценки числа факторов можно подойти со статистической точки зрения. Ранее отмечалось, что если коэффициенты корреляции после учета mфакторов незначимо отличаются от нуля, то нет необходимости вводить (m+1)-й фактор. Другими словами, равенстводолжно выполняться в статистическом смысле (здесь− матрица факторных нагрузок с числом факторов, равнымm). Для оценки значимости матрицыR(в самом начале факторного анализа) либо матрицыиспользуется критерий Бартлетта − Уилкса

с n(n-1)/2степенями свободы, либо его аппроксимация, где– элементы матрицы.

Если все эти критерии дают не противоречащие друг другу решения, то удовлетворяются этими mфакторами.

Метод максимального правдоподобия. В этом методе по выборочной корреляционной матрицеисходных признаков ищутся состоятельные и эффективные оценки неизвестных параметров − элементов матрицВиWдля генеральной совокупности. При построении функции максимального правдоподобия существенно используются предпосылки факторного анализа. Максимизация функции правдоподобия приводит к множественности результатов. Неоднозначность обходится требованием, чтобы матрица

(11.9)

имела диагональный вид. Это условие соответствует требованию метода главных факторов о взаимной ортогональности факторов и их ориентации по направлению максимума дисперсии.

Система (11.9) может быть приведена к виду, удобному для вычислений итерационным путем:

. (11.10)

Скорость сходимости итерационной процедуры является весьма медленной и зависит от начального приближения BиW.

В методе максимального правдоподобия проблема определения числа факторов также существует. Пусть расчеты по (11.10) проведены для mобщих факторов. Для проверки гипотезы о существованииmобщих факторов можно воспользоваться критерием

cстепенями свободы.

В этой формуле – определитель матрицы корреляций, воспроизведенных с помощьюmобщих факторов. Если вычисленное значение критерия превышает табличное значениепри выбранном уровне значимости, то необходимо выделить факторов больше, чемm, по крайней мере ,m+1.

Оценка общностей. Проблемы оценки общностей и оценки факторов тесно переплетаются. Если значения общностей установлены, то матрицастановится полностью известной и для нее может быть установлен ранг, т.е. минимально необходимое число общих факторов. Если вначале установлено числоmобщих факторов, то значения общностей подбирают таким образом, чтобы ранг матрицыприближался к этому числу. Существует несколько способов оценивания общности. Мы их рассмотрим вкратце, поскольку при большом числе переменных точность оценивания общностей практически не сказывается на результатах факторного анализа.

Наиболее теоретически обоснован и чаще всего рекомендуется в качестве оценки общности i-го признака коэффициент множественной корреляцииi-го исходного признака с остальными (n–1) признаками.

Значение вычисляется по формуле:, (11.11)

где – диагональный элемент обратной корреляционной матрицы.

При проведении факторного анализа на ЭВМ во многих случаях используют итерационную процедуру вычисления общностей. На каждой итерации с помощью метода главных факторов определяют матрицу факторных нагрузок, а по ней находят оценки общностей, которые используются в следующей итерации. В качестве начaльного приближения используют коэффициент множественной корреляции (11.11).

Вращение факторов. Исследование с помощью факторного анализа следует признать успешным, если выявлено не только число общих факторов, но и дано содержательное толкование тем внутренним, скрытым причинам (общим факторам), которые обусловили результаты наблюдений. С целью облегчения процесса интерпретации общих факторов осуществляется третий этап факторного анализа – вращение факторов. Выше указывалось, что матричное уравнениеимеет бесконечное число решений (с точностью до ортогонального преобразованияТ). Рассмотренные методы выделения факторов однозначно устанавливают положение системы координат, однако за счет введения дополнительных ограничений. Оси, соответствующие общим факторам, ориентируются последовательно по максимуму оставшейся дисперсии. Такая ориентация координат оказывается существенной в методе главных компонент, ориентированном на дисперсии. Основная цель факторного анализа – объяснение корреляций между исходными признаками. Окончательную ориентацию осей координат здесь производят из других соображений, а именно: с точки зрения содержательной интерпретации общих факторов. Для этого систему координат в пространстве общих факторов поворачивают как целое вокруг ее начальной точки, что эквивалентно умножению факторного отображенияВна ортогональную матрицуТсправа.

Процедуру вращения рассмотрим на примере. По результатам успеваемости построена корреляционная матрица оценок по шести предметам: математике, физике, истории, литературе, родному языку, иностранному языку. Одним из методов выделены два общих фактора. Корреляционная матрица и матрица факторных нагрузок приведены в табл.26.

Таблица 26

№ признака	Корреляционная матрица						Общий фактор1	Общий фактор2
1	1	0,50	0,32	0,20	0,22	0,12	0,6	0,6
2	0,50	1	0,21	0,15	0,16	0,07	0,4	0,4
3	032	0,21	1	0,44	0,67	0,41	0,7	0,2
4	0,20	0,15	0,44	1	0,56	0	0,6	-0,2
5	0,22	0,16	0,67	0,56	1	0,51	0,8	-0,4
6	0,12	0,07	0,41	0,33	0,51	1	0,5	-0,3

Интерпретация полученных общих факторов представляет определенные трудности: необходимо выявить то общее, что обусловило высокие нагрузки на все шесть предметов у первого фактора, и на первый, второй и пятый – у второго, причем последняя значимая нагрузка − отрицательна.

На рис. 14 приводится графическая иллюстрация полученного факторного отображения (номера точек 1-6 соответствуют строкам матрицы факторного отображения).

Рис.14. Поворот системы координат

Повернем оси координат по часовой стрелке так, чтобы сгусток, состоящий из точек 3-6, оказался как можно ближе к оси . Угол поворотасоставляет как видно из рисунка,. Матрица преобразованияTкоординат при повороте на уголпо часовой стрелке имеет вид:.

Новые координаты точек В_нполучаются перемножением матрицВиT, т.е.. (11.12)

Для рассматриваемого примера получим: .

Интерпретация факторов, отвечающих матрице , несомненно проще: первый фактор существенно нагружает теперь только четыре исходных признака (история, литература, родной и иностранный языки), а второй первые два признака (математика, физика), причем значимых отрицательных нагрузок нет. Естественно первый фактор назвать, например, гуманитарной одаренностью, а второй – склонностью к точным наукам.

Рассмотренный пример явился иллюстрацией геометрического подхода к проблеме вращения. Он предполагает визуализацию факторного отображения с последуюшим поворотом системы координат так, чтобы новые оси проходили через скопления точек. Если число общих факторов больше двух, то вращение осуществляется по шагам, учитывая каждый раз одновременно только две оси. Полная матрица преобразования состоит из произведения отдельных матриц преобразования для всех комбинаций пар факторов.

Только что рассмотренный пример на вращение показывает, что интерпретация общих факторов тем проще, чем «контрастнее» будут значения нагрузок – элементы столбца матрицы факторного отображения: либо близки к нулю, либо к единице. В этом случае каждый исходный признак получает наиболее простое описание на языке общих факторов (11.10) и, наоборот, при интерпретации каждого общего фактора учитывается минимальное число исходных признаков. Именно эти соображения легли в основу концепции простойструктуры,широко используемой в факторном анализе. Термин «простая структура» служит для характеристики взаимосвязи между конфигурацией векторов, соответствующих исходным признакам, и осями координат пространства общих факторов. Если конфигурация векторов такова, что позволяет вращением координат достигнуть положения, при котором значительное большинство векторов-признаков окажутся на гиперплоскостях координат или вблизи них, то в этом случае говорят о простой структуре.

При многомерном факторном анализе в каждом столбце матрицы факторных нагрузок Bнайдутся несколько элементов, близких к нулю. Отсюда возникает вопрос: какое количество нулевых нагрузок достаточно, чтобы считать найденную гиперплоскость значимой? Решить этот вопрос можно с помощью критерия Баргмана. Для очередногоi-го общего фактора подсчитывают числопризнаков, для которых выполняется условие. Это число, называемое числом нулевых нагрузок, сравнивают с табличнымq_Т, соответствующим определенному числу исходных признаков. Еслипри выбранном уровне значимости, то этот фактор считается определенным и его можно интерпретировать. Критерий Баргмана проверяет по сути дела гипотезу, что векторы, отвечающие исходным признакам, лежат друг к другу плотнее, чем можно было бы ожидать при случайном их расположении в пространстве общих факторов.

Кроме геометрического подхода к вращению факторов применяется аналитический подход. Применение этого подхода потребовало выработки критерия, с помощью которого можно было бы сравнивать результаты вращения.

Такой критерий опирается на концепцию простой структуры. В качестве меры простоты фактора выбирается дисперсия квадратов его нагрузок. Если эта дисперсия максимальна, то отдельные нагрузки близки к нулю или единице. Взяв сумму дисперсии по всем факторам и приводя векторы-признаки к единичной длине, получаем так называемый варимакс-критерий:.

Процедура вращения осуществляется последовательно, учитывая каждый раз только две оси. Производится поворот на некоторый небольшой угол. Факторные нагрузки пересчитываются по формуле (11.12). Если при этом значение варимaкс-критерия возрастает, то эти оси вновь поворачиваются на тот же самый угол. Если же значение варимакс-критерия уменьшится, то переходят к другой паре координатных осей, и процедура повторяется.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3

Схема двухфакторного ДА.

Схема двухфакторного анализа.

Исследуемая переменная уопределяется теперь двумя факторамиA иВсpиqуровнями соответственно. На каждой изpqкомбинаций уровней доступно по одному наблюдению. ДляN=pqвыборок единичного объема постулируется модель,

где m, a_i, b_j– параметры,u_ij– случайная компонента с теми же свойствами, что и в однофакторном ДА. Условий репараметризации здесь два:.

Применяя МНК, находят оценки параметров: ,,

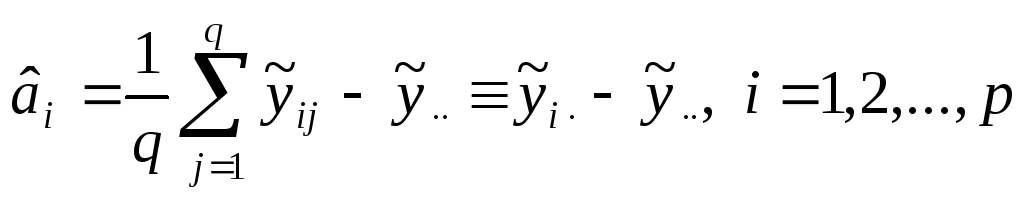Основная задача двухфакторного ДА – проверка равенства нулю параметров a_iиb_j, т.е. проверка гипотез:Н_А: а₁=а₂=…=а_р=0 иН_В:b₁=b₂=…=b_q=0.

Как и в однофакторном ДА, общую сумму квадратов S₀отклонений от общего среднего можно разложить на составляющие – теперь уже три:S_A=,S_B=, обусловленные изменчивостью между уровнями факторовАиВсоответственно, плюс слагаемое, связанное со случайной составляющей (экспериментальная ошибка).

Схема вывода соотношения S₀=S_A+S_B+S_R (5.5) та же, что и в однофакторном ДА.

За основу положено тождество: .

Исходные данные и результаты двухфакторного ДА принято представлять в виде табл.13 и 14.

Таблица13

Уровни фактора А	Уровни фактора В	Среднее по строкам
Уровни фактора А	1 2 … q	Среднее по строкам
1 2 p	… … …
Среднее по столбцам	…

Таблица 14

Источник изменчивости	Сумма квадратов	ЧСС	Среднее квадратов	F-отношение
Фактор А	S_A	p-1
Фактор В	S_B	q-1
Ошибка	S_R	(p-1)(q-1)
	S₀	pq-1

Гипотеза Н_А(Н_В) считается приемлемой, еслиF_AF_Т_А(F_ВF_Т_В), гдеF_Т_А,F_Т_В– табличные значенияF-распределения с ЧСС числителя и знаменателя в соответствии с табл.14.

Концепция «простой структуры в факторном анализе.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4

Экспериментальные критерии планирования эксперимента.

Экспериментальные критерии планирования эксперимента.

Все многообразие критериев планирования эксперимента можно разбить на две большие группы

Вторую группу составляют критерии, зародившиеся в практике планирования эксперимента и ориентированные на удобство расчетов и организации проведения экспериментов (критерии ортогональности и композиционности).

Смысл перечисленных критериев можно пояснить, используя понятие эллипсоида рассеяния случайного вектора. Для случайного вектора аразмерности, ковариационная матрица которого естьcov a, эллипсоид рассеяния задается выражением ,

описывающим эллипсоид в -мерном пространстве с центром в точкеМа. Эта геометрическая фигура имеет такие размеры, что ковариационная матрица случайного вектора, равномерно распределенного в пределах эллипсоида, совпадает с матрицейcov a. Следовательно, чем больше рассеяние вектора относительно его математического ожидания, тем большие размеры имеет эллипсоид рассеяния.

Критерий ортогональностиКритерий ортогональности требует выбора плана, обеспечивающего диагональность информационной матрицы. Использование этого критерия имеет целью упростить вычисления и обеспечить независимость оценок коэффициентов регрессии.

Критерий композиционности Критерий композиционности требует выбора плана, который включал бы в себя точки оптимального плана моделей более низкого порядка. Это обеспечивает сокращение числа опытов при поэтапном усложнении модели.

На практике желательно использовать планы, удовлетворяющие одновременно нескольким критериям. В общем случае такого сочетания свойств не наблюдается. В теории планирования эксперимента доказано, что непрерывный D-оптимальный план является такжеG-оптимальным. УсловиеD-оптимальности дискретного планаимеет следующий вид: . (6.2)

Если для дискретного D-оптимального плана имеет место, то этот план является такжеA-оптимальным.

Построение D-оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия отпеременных для стандартной области (гиперкуб)). В общем случае для построенияD-оптимальных планов используются численные методы, связанные с минимизацией определителя матрицыСлибо максимизацией определителя информационной матрицыF’F, что несомненно проще в вычислительном отношении.

Выделение факторов в факторном анализе.

, (11.7)

. (11.8)

Сравнивая (11.6) и (11.8), получаем, что в качестве оценки матрицы Вможно взять матрицу.

Рассмотрим матрицу .Справедлива следующая цепочка равенств:.

с n(n-1)/2степенями свободы, либо его аппроксимация, где– элементы матрицы.

Если все эти критерии дают не противоречащие друг другу решения, то удовлетворяются этими mфакторами.

(11.9)

Система (11.9) может быть приведена к виду, удобному для вычислений итерационным путем:

. (11.10)

cстепенями свободы.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5

Теоретические критерии планирования эксперимента.

Теоретические критерии планирования эксперимента.

Все многообразие критериев планирования эксперимента можно разбить на две большие группы. Первую составляют критерии, непосредственно учитывающие точностные свойства получаемых оценок. Среди них можно выделить критерии, связанные с точностью нахождения коэффициентов регрессии (критерии A- иD-оптимальности), и критерии, требующие максимальной точности оценки выходной переменной (критерийG-оптимальности).

Критерий А-оптимальности Поскольку точностной характеристикой вектора коэффициентов регрессии является ковариационная матрица, а критерии планирования желательно иметь в скалярной форме, то необходима некоторая свертка ковариационной матрицы. Критерий A-оптимальности в качестве такой свертки использует след матрицы. Поскольку диагональные элементы матрицыСпропорциональны дисперсии оценок коэффициентов регрессии, то при минимизации следа матрицыСминимизируется, по сути дела, суммарная либо средняя дисперсия оценок коэффициентов модели: .

Известно, что сумма диагональных элементов матрицы равняется сумме её собственных значений. Поскольку квадраты длины осей эллипсоида рассеяния пропорциональны собственным значениям ковариационной матрицы, то критерий A-оптимальности требует минимизации диагонали параллелепипеда, описанного у эллипсоида рассеяния.

Критерий D-оптимальности КритерийD-оптимальности требует такого расположения точек в области планирования, при котором определитель матрицыимеет минимальную величину. Иными словами, планD-оптимален, если .

Известно, что объем эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е.. С учетом (3.8)V.

Чем меньше величина определителя, тем меньше, как правило, разброс оценок коэффициентов относительно их математических ожиданий. Исключением является случай, когда эллипсоид рассеяния имеет сильно вытянутую форму.

Критерий G-оптимальности ПланG-оптимален, если он обеспечивает наименьшую величину максимальной дисперсии оценки зависимой переменной:.

Меры близости в кластерном анализе.

Меры близости и различия в кластерном анализе.

Функции расстояния и сходства Неотрицательная вещественная функция называется функцией расстояния (метрикой), если:

а) для всехииз;

б) лишь для;

в) ;

г) , где− любые три точки из(так называемое “правило треугольника”).

Значение функции dдля двух заданных точекэквивалентно расстоянию междуОⁱиО^j.

В качестве примера функций расстояний приведем наиболее употребительные:

евклидово расстояние ;

2) сумма абсолютных отклонений, называемая иногда метрикой города, ;

3) расстояние Махаланобиса ,

где – матрица, обратная матрице рассеяния (см. (9.3)) .

Расстояние Махаланобиса часто называют обобщенным евклидовым расстоянием; оно инвариантно относительно невырожденного линейного преобразования Υ=BХ, то есть.

Первые две метрики представляют частный случай так называемой -метрики:

Для -метрики справедливо соотношение для любыхтогда и только тогда, когда.

Обобщением l_p-метрики является «взвешенная»l_p-метрика,

где w_i– некоторый неотрицательный «вес», пропорциональный степени важностиi-й компоненты при решении вопроса об отнесении объекта к тому или иному классу.

Расстояния между Nобъектами могут быть сведены в квадратную симметричнуюматрицу расстояний

. (9.2)

Понятием, противоположным расстоянию, является понятие сходства. Мерой сходства называют неотрицательную вещественную функцию, удовлетворяющую следующим аксиомам:

1) ;

2) ;

3) .

Значения функции сходства элементов множества Оможно объединить в матрицу сходства

Величину обычно называют коэффициентом сходства. Приведем в качестве примера функции сходства для объектов, описываемых дихотомическими признаками, т.е. такими, которые могут принимать значения нуль или единица. Для заданных точекиобозначим черезчисло совпадающих единичных (нулевых) координат, через– число координат, имеющих 1 ви 0 в, сходным образом определяется. Мерами сходства будут функции:

1) ; 2); 3).

Заметим, что подбирая подходящее преобразование, можно перейти от мер расстояния к мерам сходства.

Меры близости и расстояния могут задаваться также с помощью так называемых потенциальных функцийF(U,V) = f(d(U,V)),гдеUиV– любые две точки изЕ_n,d(U,V) – метрика. В качестве примера приведем две такие функции:F(U,V) = exp (– ad²(U,V)), a>0;F(U,V) = (1 + ad²(U,V))^-¹.

Выбор той или иной метрики (или меры близости) является ответственным этапом кластерного анализа, оказывая существенное влияние на результаты разбиения объектов на классы. В каждой конкретной задаче этот выбор должен производиться с учетом целей исследования, физической и статистической природы наблюдений, полноты априорных сведений о характере распределения наблюдений. Приведем несколько рекомендаций по выбору метрики.

1. Если известно, что наблюдения извлекаются из нормальных генеральных совокупностей с одной и той же матрицей ковариаций, то целесообразно использовать расстояние Махаланобиса.

2. Использование обычного евклидова расстояния можно признать оправданным, если:

а) компоненты вектора наблюдений взаимно независимы и имеют одну и ту же дисперсию;

б) отдельные признаки однородны по физическому смыслу и одинаково важны с точки зрения задачи классификации;

в) пространство признаков совпадает с геометрическим пространством (n= 1, 2, 3).

В некоторых задачах связи между объектами вытекают из сущности самой задачи, требуется лишь «подкорректировать» их с тем, чтобы они удовлетворяли аксиомам мер расстояния или сходства. Примером может служить задача классификации с целью агрегирования отраслей народного хозяйства, решаемая на основе матрицы межотраслевого баланса.

Рассмотрим теперь меры близости между кластерами. Введение понятия расстояния между группами объектов оказывается целесообразным при конструировании многих процедур кластеризации. ПустьК_i–i-й кластер, содержащийобъектов;– арифметическое среднее наблюдений, входящих вK_i, т.е.– выбранная метрика.

Рассмотрим наиболее употребительные расстояния между кластерами:

1) расстояние, измеряемое по принципу ближайшего соседа (nearest neighbour)

;

2) расстояние, измеряемое по принципу дальнего соседа (furthest neighbour)

;

3) статистическоерасстояние между кластерами ;

4) расстояние, измеряемое по центрам тяжестикластеров.

Легко видеть, что пропорционально, если в качестве метрики используется евклидово расстояние;

5) мера близости, основанная на потенциальной функции F(K_l,K_m) =

Иллюстрация трех приведенных мер представлена на рис. 8.

Рис.8. Примеры расстояний между кластерами

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6

Регрессионный анализ факторного эксперимента.

Регрессионный анализ факторного эксперимента.

Этапы факторного анализа Вычислительный аспект факторного анализа связан с определением факторного отображенияВ, дисперсий характерных факторов и оценкой значений общих факторов. Оценка этих параметров производится на основании экспериментальных данных, полученных в ходе наблюдений надNобъектами (индивидами). Результаты наблюдений представляются в виде матрицы исходных данных, аналогичной (11.1). По матрицеХвычисляется корреляционная матрицаR. Затем начинаются этапы собственно факторного анализа. Первый этап – оценка общностей. Если общности оценены, то по формуле (11.5) можно оценить характерности, а следовательно, и матрицуW, которая является диагональной согласно предпосылкам факторного анализа. Заменяя диагональные элементы матрицыRна оценки общностей, получают матрицу, которая является информационной основой второго этапа выделения факторов. На этом этапе решают тем или иным способом матричное уравнение, получая в итоге ортогональную матрицуA. Возможно большое число матрицA, которые одинаково хорошо будут воспроизводить матрицу. Из них должна быть выбрана одна, что составляет содержание третьего этапа – вращения факторов. И, наконец, на последнем, четвертом, этапе оцениваются значения факторов для каждого объекта (индивида). На практике, однако, из-за большого объема вычислений часто ограничиваются первыми тремя этапами, причем первый и второй выполняются одновременно.

Метод главных факторов.Как следует из фундаментальной теоремы факторного анализа (11.3),. Приравняем вначалеWнулевой матрице. Получим матричное уравнение(11.6)