Тема 3. Производные и дифференциалы. Экстремумы функции одной переменной

Содержание

1. Определение производной.

2. Геометрический и экономический смысл производной.

3. Основные правила дифференцирования.

4. Таблица основных формул дифференцирования.

5. Производные высших порядков.

6. Вычисление пределов с помощью производных.

7. Дифференциал функции.

8. Свойства дифференциала.

9. Применение дифференциала к приближенным вычислениям.

10. Дифференциалы высших порядков

11. Монотонность функции.

12. Экстремумы (максимумы и минимумы) функции.

13. Наименьшее и наибольшее значения непрерывной функции на отрезке.

1. Определение производной

Определение производной функции.

Пусть функция определена и непрерывна в некоторой окрестности точки. Придадим значениюприращение, получим точку(величина-приращение аргумента).

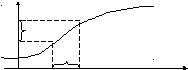
Приращением функции называется разность значений функции .

0

• Производной функции 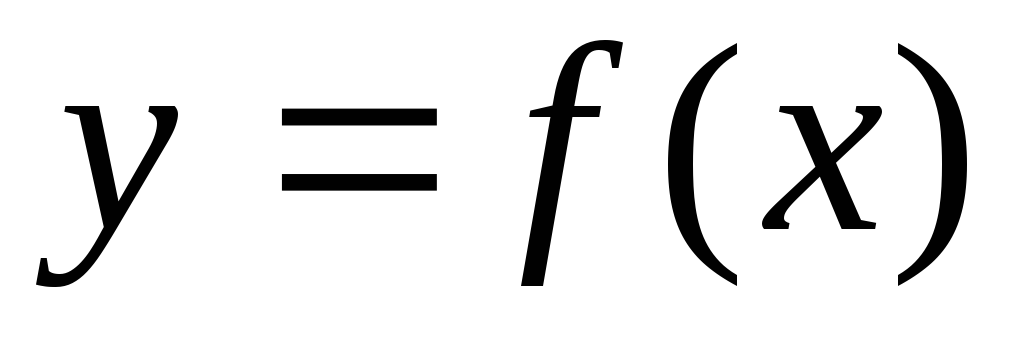в точке называется предел отношения приращения функциик вызвавшему его приращению аргументапри произвольном стремлениик нулю, если такой предел существует и конечен:

.

Обозначается производная ,,.

Число показываетизменение функции при бесконечно малом изменении аргумента относительно .

• Операция нахождения производной называетсядифференцированием функции .

• Функция 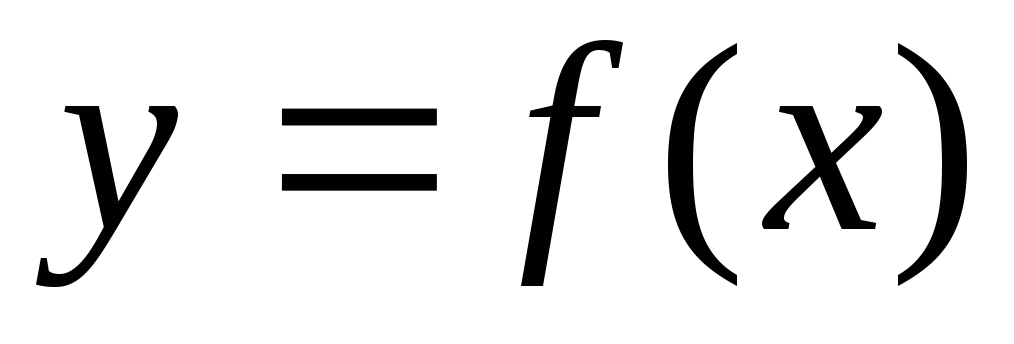, имеющая производную, называетсядифференцируемой.

Для любой ли функции существует производная?

ТЕОРЕМА. (О связи между дифференцируемостью и непрерывностью функции)

Если функция дифференцируема в точке, то она непрерывна в этой точке.

Доказательство. Пусть в точкесуществует производная_. Покажем, чтонепрерывна. Еслито и а это и означает, что непрерывна в точке.

Замечание.Эта теорема определяет лишь необходимое условие существования производной, т.е. из дифференцируемостивытекает ее непрерывность. Обратное неверно, т.к. существуют непрерывные функции, которые в некоторых точках являются дифференцируемыми.

Пример.Функция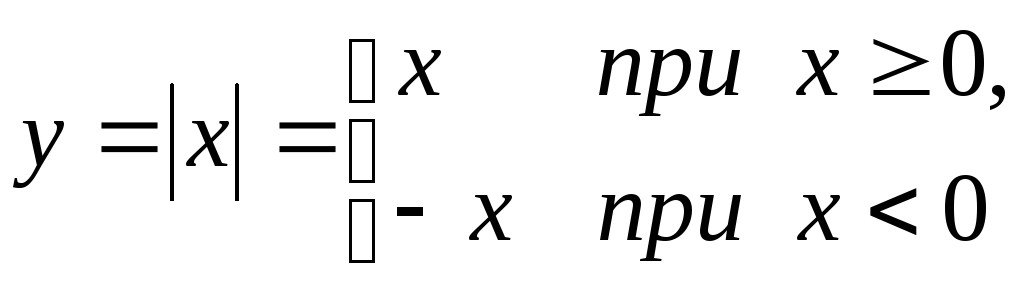непрерывна в точке, но не дифференцируема в этой точке, так как левостороння производная равна (-1), а правосторонняя равна 1, то есть существуют, но не совпадают.

2. Геометрический и экономический смысл производной

2.1. Геометрический смысл производной и уравнение касательной

Рассмотрим график функции .

Касательной к графику функции в точкеназывают предельное положение секущейпри произвольном стремлении точкик точкепо графику функции.

Касательная прямая к графику в точке образует с осью ОХ угол- это угол между положительным направлением осии касательной, отсчитываемый против часовой стрелки.

Значение производной функции в точке равно угловому коэффициенту касательной, проведенной к графику функциив точке с координатами.

Значение производной равно тангенсу угла между положительным направлением осии касательной:.

0

Уравнение касательной к графику функции в точкеимеет вид:.

Пример. Записать уравнение касательной к графику функции в точке с абсциссой.

При значение функции. Производная, значение производной.

Уравнение касательной примет вид , или.