глава2

где kα-1=D – коэффициент макродиффузии, м2/с.

В уравнении (2.10) лишь одна неизвестная функция w(ρ, x, t), которая определяется однозначно по известным начальным и граничным условиям. Далее по любому из уравнений можно определить vx(ρ, x, t).

Уравнение (2.10) не может быть отнесено к какому-либо типовому классическому уравнению математической физики. Это довольно характерно для обогатительных аппаратов. Для их решения могут быть использованы численные методы.

Одним из важных практических применений решения уравнения сепарации является теоретическое вычисление сепарационных характеристик аппаратов.

Фракционный состав концентрата получают усредняющим интегрированием функции состояния по зоне концентрата с объемом Vк (в стационарном режиме):

wк(ξ) = Vк−1 ∫ ∫∫w(ξ, x, y, z)dV.

Vк

Аналогично получают фракционный состав для хвостов. Для аппарата справедливо уравнение баланса:

Qисхwисх(ξ)= Qкwк(ξ)+ Qхwх(ξ)

где Qисх, Qк, Qх – производительность аппарата по исходному питанию, концентрату, хвостам. Тогда сепарационная характеристика может быть вычислена по

формуле

εк(ξ) Qкwк(ξ()ξ)

Qисхwисх

В дальнейшем на конкретных примерах различных обогатительных аппаратов методика будет рассмотрена более подробно.

2.2.7. Модели, получаемые структурными преобразованиями

Для линейных (линеаризованных) элементов, соединенных в какую-либо схему, в теории автоматического управления разработан аппарат структурных преобразований. Задача сводится к тому, чтобы при известных передаточных функциях элементов (звеньев) получить передаточную функцию системы (схемы). Такой подход имеет существенное ограничение – он не применим для нелинейных элементов.

Если процесс разделения с получением двух продуктов представить как два звена с общим входом и разными выходами, соответствующими концентрату и хвостам, т. е. ввести эквивалентную схему замещения процесса разделения, то с помощью полученных звеньев можно изобразить любую схему соединения разделительных процессов. Каждое звено имеет свою передаточную функцию: по каналу концентрата Wк, по каналу хвостов Wx = 1 – Wк. Передаточная функ-

41

ция – это либо передаточный коэффициент k (показатель обогащения – извлечение, выход), либо линейное уравнение, связывающее k с каким-либо параметром р (время, расход реагентов, плотность разделения и т. п.): k=a0 + a1p.

Ценность метода состоит в том, что сложную блок-схему процесса можно путем преобразования упростить, вплоть до одного звена, сопровождая преобразование получением передаточной функции схемы в целом. Конечная передаточная функция – это формула схемы, по которой можно вычислить конечные технологические показатели, задаваясь аналогичными показателями в элементарных звеньях.

Алгоритмическая структура любой схемы представляет собой комбинацию трех типовых соединений элементов – последовательного, параллельного и встречно-параллельного (рис. 2.24). При этом замена нескольких звеньев одним производится по формулам:

Рис. 2.24. Последовательное (а) и параллельное соединения звеньев; в – встречно-параллельное соединение (циркуляция)

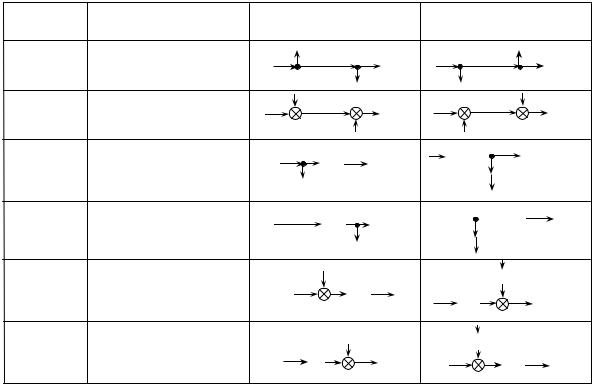
Если схема имеет перекрестные обратные связи, необходимо использовать дополнительные правила структурных преобразований (рис. 2.25).

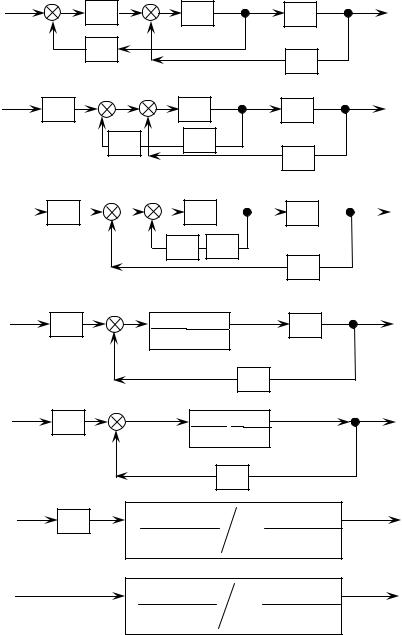
Применение перечисленных правил рассмотрим на примере. Пусть имеется схема соединения элементов (рис. 2.26, а), полученная заменой разделительных операций эквивалентными звеньями, каждое из которых определенно передаточным коэффициентом. Методом структурных преобразований предельно упростим схему и получим ее формулу. Упрощение и получение формулы ведется в несколько этапов. Сначала, пользуясь правилом 5 (рис. 2.26,6), перенесем узел суммирования 1 на выход звена k1i далее, пользуясь правилом 2, поменяем местами узлы суммирования 1 и 2 (рис. 2.26, в). В результате схема перестает быть перекрестной. Затем, используя правила свертывания контуров, последовательными шагами (рис. 2.26, г, д, е, ж) приходим к однозвенной схеме со сложным передаточным коэффициентом – формулой схемы. Возможны и другие варианты преобразований.

42

Рис. 2.25. Правила переноса точек

Описанный аппарат теории структурных преобразований схем позволяет применять аналитические методы расчета, например, для вычисления показателей обогащения сложных технологических схем флотации.

2.3.Модели, не поддающиеся аналитическому описанию

вцелом или конечном виде

2.3.1.Цифровые модели

Втех случаях, когда возможно аналитическое решение системы уравнений математического описания, то есть перевод с помощью математических преобразований модели из первоначального вида в конечный, удобный для использования вид, модель можно получать в виде формулы, именно конечная формула используется для последующего моделирования и получения численных результатов.

Однако не всегда исходное уравнение модели удается привести аналитическим путем к удобной для непосредственного использования формуле. Иногда – это уравнения, не поддающиеся решению известными методами математики. К таким, прежде всего, относятся неинтегрируемые дифференциальные уравнения, системы дифференциальных уравнений, некоторые дифференциальные уравнения в частных производных, ряд рекуррентных соотношений. В других случаях уравнения, решаемые в принципе, не удается привести к удобному виду.

Тогда прибегают к численным решениям по первоначально записанным уравнениям модели. Для этого выбирают численный метод решения и состав-

43

44

выраженную формулой, уже после решения основной неформализуемой модели численными методами. Поскольку конечная цель создания любой модели – получение информации при моделировании, т. е. численных значений функции, рассчитанных по модели при заданных значениях аргументов, при непосредственном использовании численных моделей этап получения конечной формулы модели может отсутствовать, мы сразу имеем численный результат.

Наиболее наглядно конечная информация численной модели выражается графическими зависимостями значений функций от значений аргументов. Если модель – функция нескольких аргументов, то для ее представления используют номограммы.

2.3.2. Алгоритмические модели

Часто математическую модель сложной системы сразу составляют в виде алгоритма. Обычно это связано с необходимостью принятия решения на какомлибо этапе расчета, с использованием разных формул при различных значениях параметров или аргументов, с применением логических или неформализуемых процедур. При моделировании на ЭВМ алгоритмические модели являются широко распространенными даже в тех случаях, когда модель может быть представлена аналитически и имеет несложный вид.

Основными требованиями к форме и содержанию записи алгоритма являются наглядность, компактность и выразительность. Наиболее удобен графический способ описания алгоритмов. Он основан на представлении отдельных элементов алгоритма графическими символами, а всего алгоритма – в виде блок-схемы. На блок-схемах внутри графических символов записываются словесно или символьно производимые действия. Степень детализации блоксхемы алгоритма зависит от его сложности и степени использования стандартных процедур. Если, например, в алгоритме есть стандартные процедуры, такие, как нахождение суммы, средних значений и т. п., то нет необходимости пооперационно показывать порядок их вычисления, достаточно внутри блока привести понятный символ процедуры.

Рассмотрим пример составления алгоритмической модели в виде блоксхемы. Предположим, фрагментом некой сложной модели является выражение:

где а1, а2, а3, а4, а5, a6, – коэффициенты модели; С1, С2 – константы.

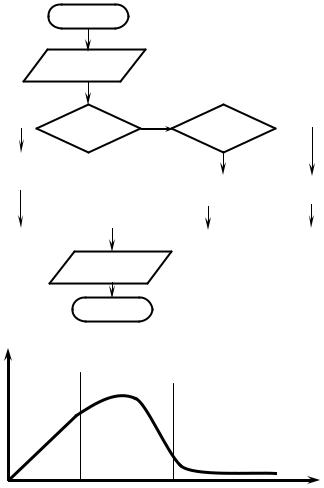
При аналитическом решении общая модель распадается на три частных, а при алгоритмическом она остается единой (рис. 2.27) и определяет функцию во всем диапазоне.

Все имитационные модели являются алгоритмическими.

45

последующих расчетов информация.

Многие методики, ввиду многокритериальности выбора той или иной справочной информации, процедуру принятия решения оставляют за человеком. При формализации методики целесообразно представлять алгоритмическими моделями. В последнее время инженерные методики проектирования автоматизируются с использованием ЭВМ, но ввиду неполной формализации строятся обычно в диалоговом режиме.

2.3.3. Декомпозиционные модели

Основная идея получения модели сложного объекта, сводящаяся к декомпозиции объекта, математическому описанию выделенных частей и последующему объединению этих моделей, может быть реализована по-разному.

Наиболее распространенным вариантом ее реализации является логическая стыковка частей модели путем последовательного расчета ее, логика которого соответствует логике развития процесса.

Если процесс во времени разбит на субпроцессы, а аппарат в пространстве на зоны, то алгоритмический принцип построения модели используется весьма часто. Исключения составляют модели, полученные объединением про-

46

стейших формул в единую без всяких условий.

В одних случаях при большом числе субпроцессов и сложном описании каждого из них итоговая формула, хотя и может быть получена, но окажется слишком громоздкой, трудновоспринимаемой и трудноанализируемой. В других случаях для описания отдельных субпроцессов могут быть получены системы дифференциальных уравнений с неявным заданием функции, аргументы и функции искомой модели в правой части, решать которые, кроме того, целесообразно численными методами. В обоих случаях составляют алгоритмические модели процесса.

Продолжим рассмотрение этого пути на примере флотационного процесса.

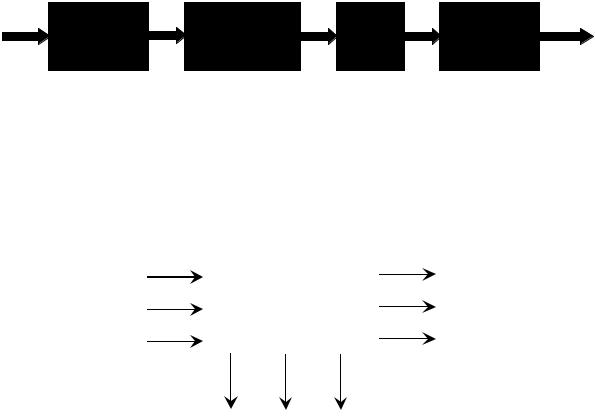
Выполним декомпозицию флотокамеры, выделив 4 последовательно совершаемые события (рис. 2.28). Кроме того, осуществим декомпозицию потока пульпы, выделив в нем фазы полезного минерала, породы и воды, каждая из которых представлена фазами крупности (а воды – фазами ионного состава). На рис. 2.29 ui; xi; Wi – фазы полезного минерала в питании, концентрате и хвостах; тj, уj, Fj – то же породы; пк; zk; Gk – то же воды.

ция на пузырьках. Потенциально возможный выход любой фазы в пену определится кинетикой процесса:

здесь Q – расход пульпы; ρi, ρj – плотность фаз; V – объем камеры; ki – коэффициент скорости флотации.

Б. Формирование пенного слоя. Пусть при некотором фиксированном расходе фаз (Σu'i + Σm'j)0 наблюдалась высота пены Н0. Тогда высоту пены будем определять пропорционально отклонению расходов фаз:

47

H = H0 (∑u′i′ + ∑m′′j) .

∑ui + ∑mj 0

Высота снимаемого пеногоном слоя будет вычисляться по формуле

hc=H – (Hш – Hп – )

где Нш – высота шибера, Нп – высота слоя пульпы под шибером, Нп= kQ2/3, – слой пены, выбрасываемой пеногоном, расположенный ниже уровня концентратного порога (рис. 2.30).

Рис. 2.30. К объяснению формирования выходящего в концентрат слоя:

а – hc≤H; б – H< hc≤H+ ; в – hc>H+

В. Формирование потока пены (съем пены), если hc≤Н (рис. 2.30, а): xi=ui'(bihc+cih2c),

если Н <hc≤Н + (рис. 2.30, б), то

xi=ui'(hc – H)riui,

если hc> Н + (рис. 2.30, в), то

xi=ui'+ riui+(Hп – Hш)ρiui.

Г. Образование потока хвостов:

Wi= ui+ xi.

Каждый из процессов логически связан с предыдущим.

Для уj, zk, Fj и Gk уравнеия имеют такую же форму, как и для xi; Wi.

В связи с наличием логических процедур задача решается алгоритмическим путем.

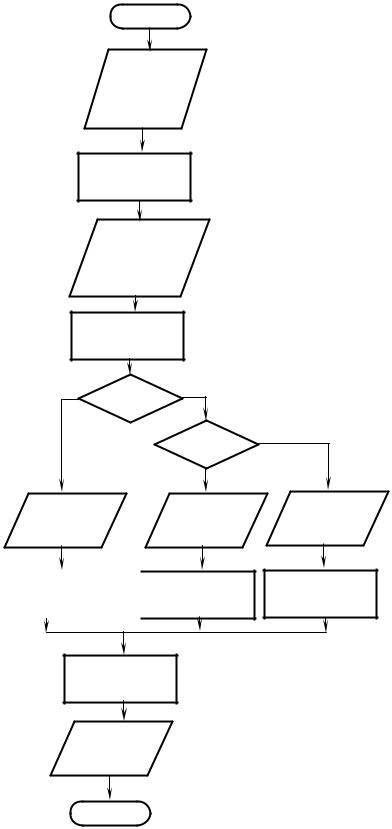
На рис. 2.31 приведена блок-схема алгоритма.

Рассмотрим декомпозиционную модель на другом примере. Пусть частица падает с некоторой высоты h(vо=0) на горизонтально вращающийся диск с угловой скоростью ω радиуса R строго параллельно оси вращения. Требуется составить модель, связывающую скорость схода частицы с диска vcx с коэффициентом трения частицы о диск, если коэффициент трения частицы о поверхность диска равен f, удар частицы о диск полагаем абсолютно неупругим, а сопротивлением воздуха пренебрегаем.

Составим модель движения частицы. Для решения воспользуемся принципом декомпозиции.

Частица проходит три фазы движения: полет до диска (рис. 2.32, а), удар о диск (рис 2.32, б), движение по диску (рис. 2.32, в). Конечные условия каждой фазы движения являются начальным условием последующей.

48

Г Wi; Fj; Gk

Вывод

Wi; Fj; Gk

конец

Рис. 2.31. Алгоритм моделирования процессов во флотокамере

49

Фаза 1. Полет до диска. Конечную скорость полета частицы до диска вычислим по формуле

ω

Рис. 2.32. К пояснению движения частицы в разных фазах:

а – падение частицы на диск; б – удар о диск; в – движение по диску

Фаза 2. Удар о диск.

При неупругом ударе по гипотезе Рауса основное уравнение динамики в

то из уравнения (2.15) записывается система уравнений движения частицы по

50