3.4. Инерционные звенья второго порядка

Дифференциальное уравнение звена

(3.34)

ему соответствуют уравнение динамики в изображениях по Лапласу

(3.35)

и передаточная функция

(3.36)

Характеристическое уравнение звена

(3.37)

имеет два корня

(3.38)

Общее решение дифференциального уравнения, определяющее свободное движение звена, имеет вид

(3.39)

Характер переходного процесса звена зависит от вида корней (3.38), которые могут быть действительными или комплексными.

Если Т₁>2Т₂, то оба корня действительные. Обозначим их

(3.40)

где Т₃иТ₄– некоторые условные постоянные времени, причёмТ₃>Т₄.

Ниже будет показано, что при Т₁>2Т₂переходная функция звена имеет монотонный, апериодический характер. Поэтому звено в этом случае называютапериодическим второго порядка.

При Т₁>2Т₂знаменатель передаточной функции (3.36) можно разложить на два множителя и представить её в следующей форме:

(3.41)

с

а

огласно которой инерционное звено второго порядка (рис. 3.6,а) можно представить как последовательное (рис. 3.6,б) соединение двух инерционных звеньев первого порядка.

б

в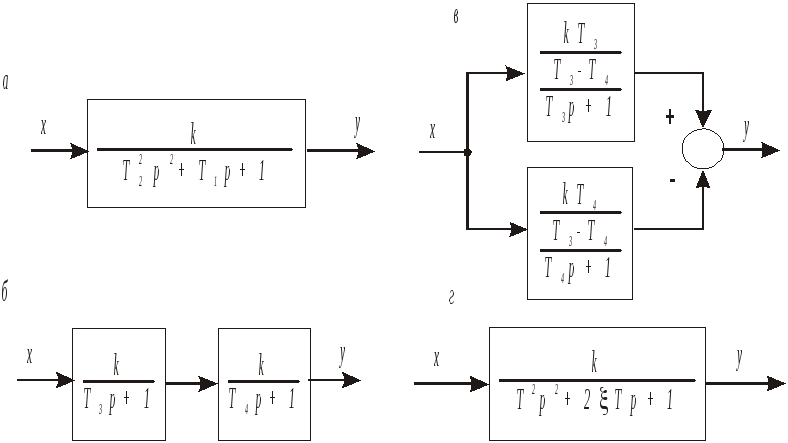

Рис. 3.6. Алгоритмические схемы инерционных звеньев второго порядка

Если Т₁<2Т₂, то корни уравнения (3.37) комплексные

(3.42)

где

Решение (3.39) в этом случае содержит гармонические составляющие, и звено называют колебательным.

Наконец, возможен случай, когда Т₁=0. При этом оба корня будут мнимыми, а переходная функция будет представлять собой незатухающую синусоиду. Инерционное звено второго порядка с Т₁=0 называется идеальным колебательным или консервативным.

Наряду с общими признаками (статизм, инерционность) апериодическое и колебательное звенья имеют и существенные различия. Рассмотрим в отдельности характеристики этих звеньев.

Переходная характеристика апериодического звена второго порядка может быть получена сложением общего решения (3.39) с частным решением, соответствующим вынужденной составляющей при x(t)=1(t). Переходная функция имеет вид

(3.43)

Временные характеристики h(t) и w(t) апериодического звена показаны на рис. 3.7, а и б. В соответствии с представлением апериодического звена второго порядка в виде последовательного соединения двух инерционных звеньев первого порядка (см. рис. 3.6,б) все его частотные характеристики (рис. 3.7,в, г, д, е) могут быть получены по аналогичным характеристикам звеньев первого порядка, приведённым в разделе 3.3 правилам умножения комплексных величин.

По графику функции А() (рис. 3.7,в) видно, что апериодическое звено второго порядка так же, как и звено первого порядка, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты.

Дифференциальное уравнение к о л е б а т е л ь н о г о з в е н а записывают обычно в следующем виде:

(3.44)

где Т=Т₂ – постоянная времени, характеризующая инерционность звена; =Т₁/2Т₂ – относительный коэффициент демпфирования, характеризующий колебательность звена (01).

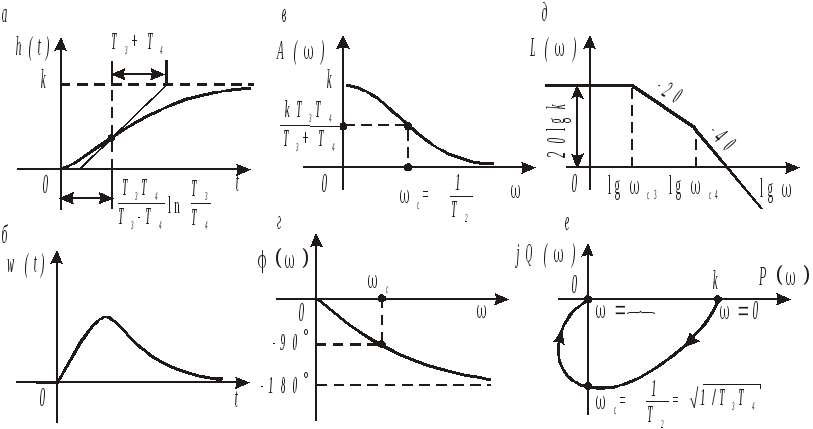
Рис. 3.7. Характеристики апериодического звена второго порядка

Передаточная функция колебательного звена

(3.45)

Корни соответствующего характеристического уравнения

(3.46)

где – коэффициент затухания;– круговая частота затухающих колебаний, рад/с.

Подставляя в общее решение (3.39) значения комплексных корней (3.46) и складывая его с частным решением k1(t), получим переходную функцию колебательного звена

(3.47)

Свободная составляющая переходной функции (рис. 3.8,а) представляет собой синусоиду, амплитуда которой убывает по экспоненциальной огибающей (пунктирная линия). Период затухающих колебаний

(3.48)

Р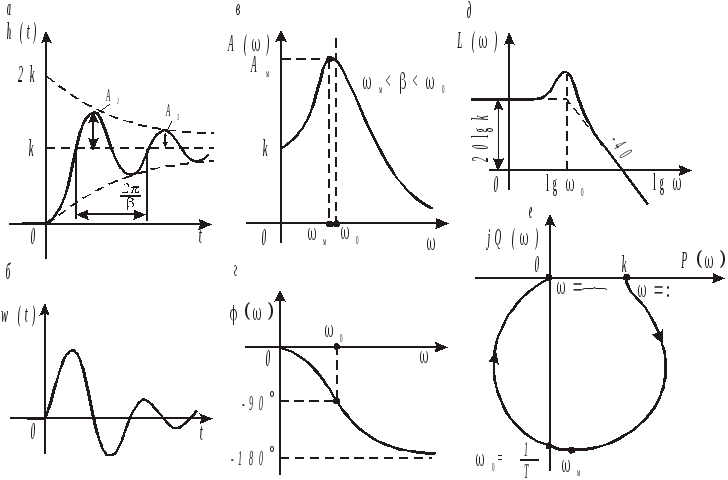ис. 3.8. Характеристики колебательного звена второго порядка

Чем больше коэффициент  и чем меньше постоянная времени Т, тем быстрее затухают колебания.

Если коэффициент демпфирования =0 (что соответствует Т₁=0), то на выходе звена после подачи единичного ступенчатого воздействия возникают незатухающие колебания с частотой ₀=1/Т.

Скорость затухания колебательных переходных процессов принято оценивать степенью затухания

(3.49)

представляющей собой отношение разности двух соседних амплитуд

(рис. 3.8,а) к первой из них. Чем ближе величина  к единице, тем быстрее затухают колебания.