
- •Киров 2010
- •Махнев А.С.
- •Глава I. Основы линейной алгебры
- •1. Матрицы и действия над ними
- •2. Определители второго и третьего порядка.
- •Обратная матрица
- •3. Системы линейных алгебраических уравнений
- •3.1. Формулы Крамера
- •3.2 Матричный способ решения системы линейных алгебраических уравнений
- •4. Собственные числа и собственные векторы матрицы
- •Глава 2. Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •геометрии в пространстве
- •2. Аналитическая геометрия на плоскости
- •3. Линии второго порядка
- •4. Полярная система координат
- •5. Комплексные числа
- •1. Предел функции
- •2. Непрерывность функции
- •3. Дифференцирование функций
- •4. Производные высших порядков. Правило Лопиталя.
- •5. Исследование функций
- •Задачи для самостоятельной работы
- •Основы линейной алгебры
- •Элементы векторной алгебры и аналитической геометрии. Комплексные числа
- •Введение в анализ. Дифференциальное исчисление функции одной переменной
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A BBYY |
c |
|
|||
|
|
|
|
|
|
|
||||
f (- 3) = (- 3)2 = 9; lim |
f (x)= lim 9 = 9; |
lim |
f (x) = lim x 2 = 9 . |
x®-3-0 |
x®-3-0 |
x®-3+0 |
x®-3+0 |
Так как f (- 3)= f (- 3 - 0)= f (- 3 + 0), то в точке x = -3 функция f (x)
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A B BYY |
c |
|
|||
|
|
|
|
|
|
|
||||
непрерывна.
2)x = 3 :
f (3) = 32 |
= 9; lim |
f (x) = lim x 2 = 9; |
lim |
f (x) = lim (2x +1) = 7. |
|
x®3-0 |
x®3-0 |
x®3+0 |
x®3+0 |
Так как |
f (3 - 0) ¹ f (3 + 0), то точка x = 3 является точкой разрыва |
|||
непрерывности функции f (x) первого рода типа скачка.
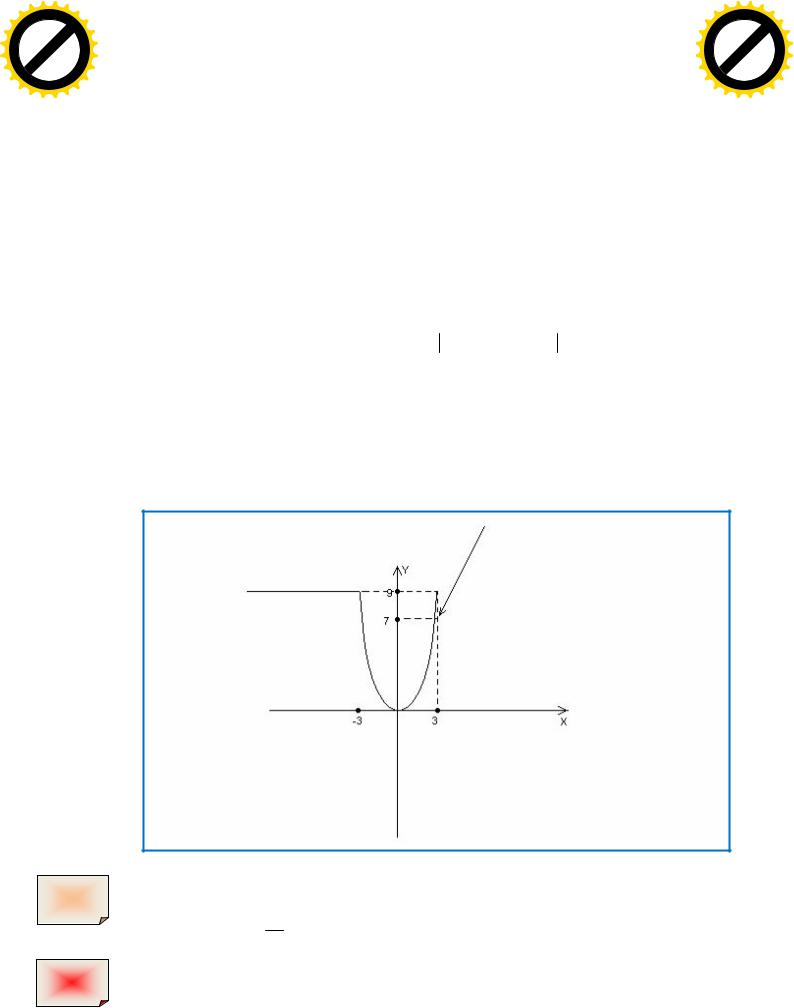
Скачок функции в точке разрыва равен: f (3 + 0)- f (3 - 0) =2. График функции
y = f (x) представлен на рисунке:
&
O
3. Дифференцирование функций
Производной y¢ = dy функции y = f (x) в точке x называется предел dx
отношения приращения функции Dy к приращению аргумента Dx , при условии, что Dx стремится к нулю.
45

AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A BBYY |
c |
|
|||
|
|
|
|
|
|
|
||||
То есть:
y ¢ = lim |
D y |
|
. |
|
D x |
||||
D x ® 0 |
|
|||
|
|
|
|
|
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A B BYY |
c |
|
|||
|
|
|
|
|
|
|
||||
Основные правила нахождения производной
Если с,a, b - const и j(x),y (x)- дифференцируемые функции в точке x , (т.е.
функции, имеющие производные в точке x ), то:
1)(с )¢ = 0 ;
2)(a ×j(x )+ b ×y (x ))¢ = a × (j(x )¢ + b ×(y (x )¢;
3) (j(x )×y x( )¢)= (j(x ))¢ ×y x( +)j x (×(y) x )¢ ( )
4) |
æ j(x )ö¢ |
(j(x )¢ ×y x( -)j x (×(y) x )¢ ( ) |
||||
ç |
|
÷ |
= |
|
. |
|
|
y 2 (x ) |
|||||
|
çy (x )÷ |
|
|
|||
|
è |
ø |
|
|
|
|
Таблица производных основных функций
1. |
(xn )¢ = nxn-1 |
|
|
|
|
|
|
|
|
|
|
|
|
8. (arctgx)¢ = |
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
|
|
|||||
2. |
(sin x)¢ = cos x |
|
|
|
|
|
|
|
|
|
|
|
|
9. (arcctgx)¢ = - |
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + x2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. |
(cos x)¢ = -sin x |
|
|
|
|
|
|
|
|
|
10. (a x )¢ = a x ln a |
(a > 0, a ¹ 1) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
(tgx ¢)= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. (ex )¢ = ex |
|
|
|
|
|
||||
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
¢ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
1 |
|
(x > 0, a > 0, a ¹ 1) |
||||||
5. |
(ctgx) = - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. (loga x) = |
|
|||||||||
sin 2 x |
|
|
|
|
|
|
|
|
|
x ln a |
|||||||||||||||||
6. |
(arcsin x)¢ = |
|
|
1 |
|
( |
|
x |
|
< 1) |
13. (ln x ¢)= |
1 |
|
|
(x > 0) |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
x |
|
|||||||||||||||||||||
1 - x2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
7. (arccos x)¢ = - |
|
1 |
|
|
|
( |
|
x |
|
< 1) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 - x2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правило дифференцирования сложной функции. Если y = f (u) и u = j(x),
т.е. y = f [j(x)], где y и u имеют производные, то
yx¢ = 46yu¢ ×ux¢
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A BBYY |
c |
|
|||
|
|
|
|
|
|
|
||||
.
Дифференцирование функции, заданной параметрически. Пусть зависимость переменной y от переменной x задана параметрически посредством параметра t :
ìx = x(t)
íîy = y(t ),
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A B BYY |
c |
|
|||
|
|
|
|
|
|
|
||||
Тогда
y x ¢ = |
yt |
¢ |
. |
|
xt |
¢ |
|||
|
|
?Задание 3. Найти производные данных функций.
1) y = 3sin x - 1 x2 2
Решение. Применяя правило 2 нахождения производных и формулы 1 и 2
таблицы производных, получаем:
æ |
|
1 |
|
2 |
ö¢ |
¢ |
1 |
(x |
2 ¢ |
)= 3cos x - |
1 |
|
|
y¢ = ç |
3sin x - |
|
x |
|
÷ |
= 3(sin x) - |
|
|
|
(2x |
)= 3cos x - x. |
||
2 |
|
2 |
|
2 |
|||||||||
è |
|
|
|
ø |
|
|
|
|
|
|
2) y = ln x 
 x
x
Решение. Применяя правило 4 нахождения производных и формулы 1 и 13
таблицы производных, получаем:
æ ln x ö¢ |
(ln x ¢) |
|
- ln x ( |
|
¢ ) |
1 |
× |
|
- ln x × |
1 |
|
|
|
|
|||||||||
|
|
|
x |
|
|
|
|||||||||||||||||
x |
x |
|
2 - ln x |
||||||||||||||||||||
x |
2 |
|
|
||||||||||||||||||||
x |
|||||||||||||||||||||||
y¢ = ç |
|
|
|
÷ |
( |
= |
|
|
2 |
) |
|
|
|
= |
|
|
|
3 = |
. |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
è |
|
x ø |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
2x 2 |
|||||||
3) y = ex ctgx.
Решение. Применяя правило 3 нахождения производных и формулы 5 и 11 таблицы производных, получаем:
x |
¢ |
x |
¢ |
|
x |
¢ |
x |
x æ |
|
1 ö |
x æ |
1 ö |
||
y¢ = (e |
ctgx) = |
e ( |
|
ctgx) |
+ e |
(ctgx) |
= e |
ctgx + e ç |
- |
|
÷ |
= e çctgx - |
|
÷ . |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
è |
|
sin 2 x ø |
è |
sin 2 x ø |
||
4) y = sin 4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Полагая |
y = sin u , где u = 4x , согласно формуле нахождения |
|||||||||||||
производной сложной функции, получим:
47
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A BBYY |
c |
|
|||
|
|
|
|
|
|
|
||||
yx¢ = (sin u)u¢ (4x x)¢ = cos u × 4 = 4 cos 4x.
AB
|
|
|
|
|
F Tran |
sf |
|
|||
|
|
|
|
D |
|
|
|
|||
|
|
Y |
P |
|
|
|
|
or |
e |
|
B |
Y |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
buy |
r |
|||
|
|
|
|
|
|
|
2 |
|||
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
to |
|
|
. |
|
|
|
|
|
|
here |
|
|
|
|
|
|
|
|
Click |
|
|
|
|
||
w |
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
||||
|
|
w |
w. |
|
|
|
|
o |
||
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
A B BYY |
c |
|
|||
|
|
|
|
|
|
|
||||
5) íìx = 2 cos t |
|
|
|
|
|
|
îy = 2 sin t |
|
|
|
|
|
|
Решение. Имеем: x |
¢ |
= (2 cos t ) ¢ |
= -2sin t; |
y |
¢ |
=(2 sin t )t ¢= 2 cos t. Тогда, согласно |
|
t |
t |
|
|
t |
|
формуле нахождения производной функции, заданной параметрически,
получаем:
y x¢ |
= |
2 cos t |
= - |
cos t |
= -ctgt. |
|
|
||||
& |
|
- 2 sin t |
|
sin t |
|
|
|
|
|||
4. Производные высших порядков. Правило Лопиталя.
Производной второго порядка функции y = f (x) называется производная от
Oее производной, т.е. (y¢ ¢). Для второй производной используются следующие
обозначения: |
y |
¢¢ |
или |
d 2 y |
, или f |
(x) |
. |
dx2 |
|||||||
|
|
|
|
|
¢¢ |
|
Производной n - го порядка от функции y = f (x) называется производная от ее производной (n -1)-го порядка. Для производной n -го порядка
используются следующие обозначения: y(n) или d n y , или f (n )(x) . dxn
Правило Лопиталя. Пусть функции f (x) и j(x) дифференцируемы в окрестности точки x0 , причем производная j¢(x) не обращается в нуль. Если функции f (x) и j(x) являются одновременно либо бесконечно малыми, либо бесконечно большими при x ® x0 , и при этом существует предел отношения
f ¢(x) при
j¢(x )
Причем
x ® x , то существует также и предел отношения |
f (x) |
|
при x ® x . |
||||||||
j(x ) |
|||||||||||
0 |
|
|
|
|
|
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) |
|
= lim |
f ¢(x) |
. |
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
j(x ) |
j (x ) |
|
|
|
||||||
|
x®x0 |
x®x0 |
|
|
|
||||||
|
|
|
¢ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Правило применимо и в случае, когда x0 = ¥ .
48
