1 Фарадеевская и Максвелловская трактовка явлений эл. магн. индукции

Если рассматривать возникновение ЭДС индукции в движущемся проводнике в этом случае ЭДС возникает благодаря силе Лоренца. Если проводник неподвижен то причиной её возникновения сила Лоренца уже не является.

По идее Максвелла изменяющееся магн. поле является порождением вихревого эл. поля, а это поле создаёт индукционный ток

Вихревое эл. Поле

Рассмотрим переменное магн. поле индукция которого изменяется

Переменное магн. поле порождает в пространстве вихревое эл. поле. Направлениевихревого эл. поля связано с направлением парвилом левого винта

2 Ток смещения. Эл. магн. поле. Уравнение Максвелла в интегральной форме

Рассмотрим плоский конденсатор с

для тока проводимости пластин

плотность тока смещения

Если в какой-то области пространства j=0, то имеется переменное эл. поле – ток смещения, то это эл. поле порождает в пространстве магн. поле линии которого связаны с направлением (dD/dt) правилом правого винта

Уравнение Максвелла в интегральной форме. Эл. магн. поле.

1)

2)

3)

4)

первое уравнение является обобщением закона эл. магн. индукции

второе уравнение является обобщением закона полного тока

третье уравнение представляет собой теорему Гаусса для диэлектрического смещения

четвёртое уравнение представляет собой теорему Гаусса для магн. индукции.

Эти уравнения дополняют три уравнения

1) D=₀E 2) B=₀H 3) j=E

Из решения этой системы следует вывод о существовании эл. магн. волн.

3. Цепи переменного тока. Импеданс.

а) перем ток в цепи с активн сопративл

U=U_mcoswt

Колеб силы тока происх в такой же фазе, что и напр.

Действ знач силы перем тока наз сила такого пост. тока которое произв такое теплов действие как и при перем токе.

б) перем ток в цепи с емкостью

U=U_mcoswt q=CU=CU_mcos wt

По ф-ле приведения: -sinwt=cos(wt+/2)

i=wCU_m cos(wt+/2)

в) пер ток в цепи с индуктивностью

U=U_mcoswt _si=-L*(di/dt) U= -_si U_mcoswt=L(di/dt)

di=(U_m/L)*coswt dt

Амплитуда:

I_m=U_m/wL => X_L=U_m/I_m=wL

г) перем ток в цепи с элементами R,C,L

Сила перем тока изм на всех участках цепи одинак.

Импеданс:

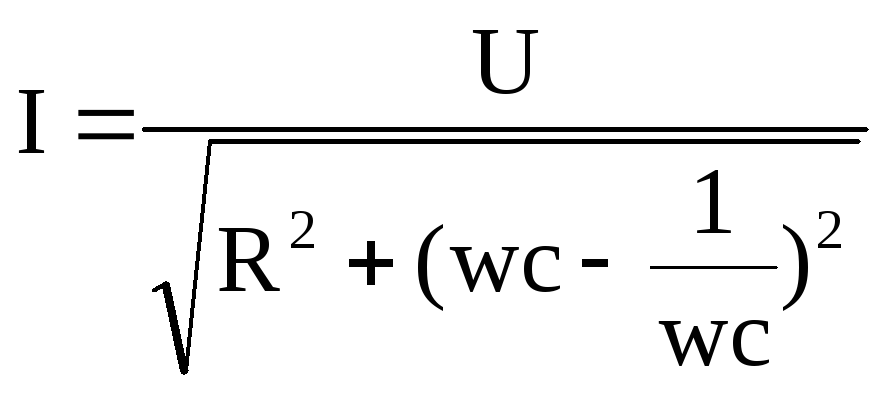
4. Гармонич. колеб.Диф. ур-е гарм. колеб. и его реш.

В колеб контуре сумма падений напряжения на индуктивности и на емкость равна нулю, поэтому Введем обознi=q и перепишем

Поскольку L м С- величины сугубо положительные, можно ввести обозн тогда

Таким образом, колеб заряда на обкладк конденсатора опи­сыв-ся лин однородным дифференциальным ур-ем второго порядка. Необходимо найти такую связь между q и t , что­бы она удовлетворяла этому уравнению. Реш дифф уравнения является выражений вида q=q_mcos=q_mcos(w₀t+₀) , где q_m,,₀ - пост, которые могут быть определены из нач условий.

Действительно, взяв вторую производную от q, по t и подставив её мы получим тождество

В уравнении qm называется амплитудой, аргумент начальной фазой колебания (при t = 0). С одинаковым правом мы могли бы написать уравнение вида

Движения, описываемые уравнениями, являются тож­дественными. 0 для каждого частного случая в этих уравнениях имеет различное значение. Из этих уравнений видно, что заряд на обкладках конденсатора изменяется по гармоническому закону, поэто­му эти уравнения называются уравнениями гармонического колебатель­ного движения. График гармонического колебания показан на рисун­ке. Величина наибольшего заряда qm на об­кладках конденсатора называется амплитудным значением заряда. Амплитуда – величина положи­тельная, фаза определя­ет состояние колеблющейся системы в каждый момент времени. Величина начальной фазы зависит от начала отсчета времени. Поскольку косинус - периодическая функция с периодом 2п, различ­ные состояния системы, совершающей гармонические колебания, повторяются через период Т, за который фаза колебаний получает приращение, равное2п, т.е. , откуда Число колебаний в единицу времени называется частотой колеба­ний. Очевидно, чтоЗа единицу частоты принимается частота такого колебания, период которого равен I с. Эту единицу называют герцем (Гц,). Используют­ся также кратные единицы: I кГц = I0³ Гц(, I МГц» = I0⁶ Гц.

Из этого следует, что

w, представляет собственную частоту колебаний контура. Она назы­вается циклической частотой и равна числу колебаний за 2п секунд. Из этих уравнений получается соотношение следует, что

Подставив, получим Разделим левую и правую части выражения на С , получим

Продифференцировав функцию по времени, получим выражение для силы тока

Сопоставив формулы, заключаем, что в момент, когда ток достигает максимального значения, заряд (а также напряжение) обращается в нуль, и наоборот. Это происходит вследст­вие того, что между током и напряжением сдвиг по фазе равен п/2.

5. Энергетические превращения происходящие при гарм - их колебаниях.

В некоторый момент времени t энергия электрического поля конденсатора равна:

А энергия магнитного поля:

Полная энергия колебания равна сумме:

Таким образом в процессе колебаний изменяется только энергия электрического и магнитного полей, полная энергия колебаний контура остается неизменной и равной наибольшей энергии конденсатора q_m²/2C или наибольшей энергии магнитного поля LI_m²/2. Энергия переходит из одного вида в другой. Обратим внимание на то что энергия колебаний пропорциональна квадрату амплитуды значений заряда или силы тока.

6. Сложение 2 гарм колеб одного напр и одинак частоты

При разл расчетах прих-ся опред переменный ток как сумму двух или нескольких переменных токов или какое-нибудь напряжение как сумму нескольких напряжений. При этом суммируемые токи или напряжения могут иметь разл амплитуды и быть сдвинутыми по фазе. Сложение их можно выполн аналитически или графи­чески, но первый способ более громоздкий.

Рассмотрим вначале, какое результ колеб получ при слож двух колеб, одинаково направленных и одинаковой частоты, имеющих разные начальные фазы и амплитуды. Пусть

(1)

Результир знач X определится как сумма:

(2)

рис 1

Выпол это сложение графич. Предст оба колеб-я векто­рами амплит. и и будем вращ их против час. стрелки с один. угло­вой скоростью w₀ (рис. 1). Тогда угол между векторами будет все время оставаться равным ₂-₁.Т.к. x=x₁+x₂,то результ колеб. может быть изоб­ражено вектором амплитуды получ геометрич сложением векторов и .

Из рис 1 имеем (3)

Таким образом, вектор со временем не меняется и вращается с угловой скоростью w₀ . Отсюда след, что результ коле­бание предст собой гармонич колеб. Нач фаза этого колеб опред из выражения:

Из формулы (3) видно, что амплитуда результ колеб зависит от разн фаз (₂-₁) слагаемых колебаний. Рас­смотрим частные случаи.

1. Разность фаз кратна четному числу  , т.е. ­₂-₁ = ±2m,

где m, = 0,1,2......

Тогда колеб происх в одинаковых фазах и ампл-х резуль­т колеб (рис.2) равна А=А₁+А₂

2. Разность фаз кратна нечетному числа  , т.е. _2­-₁=±(2m+1)

рис 2

где m - 0,1,2,.... В этом случае колебания происходят в противофазе и амплитуда резервирующ колеб (рис.3) равна А=|А₂+А₁| В частности, если А₁=А­­₂, то А=0

рис 3

т.е. колебания гасят друг дру­га.

Если разн фаз склады­в колеб имеет произ­в знач, то амплитуда результир колеб заключ в пределах

Колебания, имеяцие одинако­вые частоты и не меняющийся со временем разность фаз, называют когерентными колебаниями. Полученные результаты сложения когерент­ных гармонических колебаний будут использованы при рассмотрении явления интерференции электромагнитных волн.

7. Слож 2 гарм колеб одн направл с мало отлич частотами

Если частоты складываемых колеб неодинаковы то векторы и на векторной диаграмме будут вращаться с различной скорость. Тогда результ.вектор будет меняться по величи­не и вращ. с непостоянной скоростью. След, результ. колеб. будет негармонич.

Особый интерес представляет случай, когда два складываемых ко­лебания имеют одинаковые амплитуды и мало отличаются по частоте. Положим нач фазы колебаний равными нулю. Тогда уравнения ко­лебаний примут следующий вид: (1), где w­₂-w₁=w<<w­₁ w₂=w₁+w

Складывая выражения (1), получим x=x₁+x₂=A(cosw₁t+cosw₂t)=

(2)

рис 1 Заключ в скобки множитель в формуле (2) изменяется значи­тельно медл, чем 2 множитель. Ввиду условия w<<w за то время, за кот множитель cosw₁t совершит неск коле­б, множитель, стоящий в скобках, почти не изменится. Это дает основание рассм колебание (2) как гармоническое колеба­ние частоты w₁ , ампл котор. медленно изменяется с час­тотой по закону | 2Acos(w/2)*t | Знак модуля стоит потому, что по опред амплитуда-величина положительная. Отсюда частота колеб амплитв 2 раза превыш частоту, стоящую под знаком модуля, т.е. равна w. Уравнение (2) можно переписать в виде: (3)

График функции (3) представлен на рисунке 1

Такие колеба­ния называются биениями, а частота пульсаций амплитуда назыв частотой биения. Она равна w.