Приближенные методы поиска экстремума фмп без ограничений

Все приближенные методы поиска экстремума ФМП базируются на следующем итерационном (пошаговом) алгоритме:

, (4)

п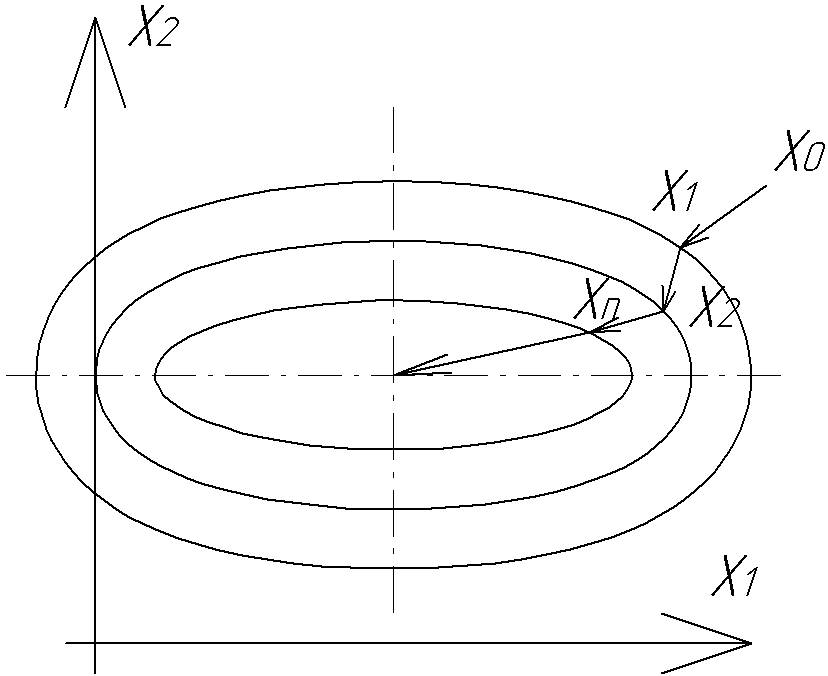о которому переход от точкина к-ом шаге к точкена (к+1)-ом шаге осуществляется в направлениис параметром шага в этом направлении^k. Естественно, что направлениеследует выбирать таким образом, чтобы приближаться к экстремальной точке. Выбор шага^kдостаточно произволен, но влияет на скорость приближения к экстремуму. Естественно, алгоритм (4) должен быть сходящимся, т.е. гарантировать попадание в экстремум за конечное или бесконечное число итераций. Такая сходимость получила название алгоритмической.

Метод Зейделя-Гаусса (покоординатного спуска)

Сущность метода

Наиболее простым приближенным методом является метод Зейделя-Гаусса. Сущность его заключается в том, что фиксируются все значения координат, кроме одной, по которой и ищется экстремум. Последовательно находя частные экстремумы по координатам за одну или несколько итераций находят приближенное значение координат точки экстремума. В математике доказывается, что метод З-Г сходится для широкого ряда функций, т.е. с его помощью за конечное число итераций можно сколь угодно близко подойти к экстремальной точке. Т.к. метод З-Г использует только необходимые условия, то с его помощью можно найти только локальный экстремум, ближайший к начальной точке. Но т.к. ранее было оговорено, что мы будем рассматривать только выпуклые и вогнутые функции, то экстремум будет глобальным.

Применение метода З-Г к сепарабельным функциям.

П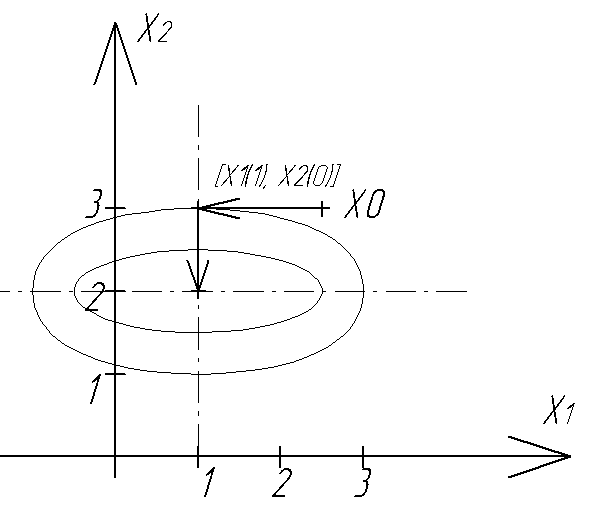усть задана функция. Ранее было показано, что это строго выпуклая функция с минимумом в точке х^*=(1, 2). Однако при использовании приближенных методов значения координат экстремума не известны (иначе задача теряет смысл). Проиллюстрируем метод З-Г на плоскости. На рисунке изображены линии уровня функции (2).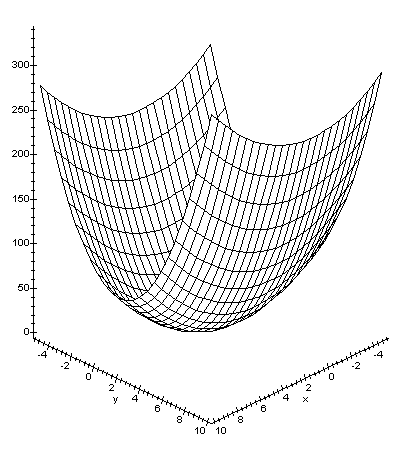

Пусть задана точка х⁰=(2,5; 3), начальная точка может быть любой, т.к на функцию не наложено ограничений. Зафиксируем координату. Это равноценно проведению в пространстве {y,x₁,x₂} плоскости П₀, параллельной плоскости {y,x₁}. Запишем уравнения функции в этой плоскости:

Следовательно, в плоскости П₀функция является параболой. Найдем координаты экстремума в плоскости П₀,. Определим значение функции при:y=4.

Теперь зафиксируем точку x₁на ее экстремальном значении, полученном на предыдущем шаге. Это равносильно проведению плоскости П₁параллельно плоскости {y,x₂}. В данной плоскости функция является параболой с уравнением:. Найдем координаты экстремума в плоскости П₁:.

Таким образом, за одну итерацию, содержащую два шага, найдено точное значение экстремума сепарабельной функции. Это объясняется тем, что главные оси эллипсов, являющихся линиями уровня, были параллельны осям x₁иx₂. Данное правило распространяется и на функцииnпеременных. Если уравнение сепарабельной функции содержитnпеременных, то для нахождения ее экстремума требуется не болееnшагов. В этом огромное преимущество метода З-Г для сепарабельных функций.

Применение метода Зейделя-Гаусса к квадратичным функциям.

Аппроксимация квадратичными функциями гораздо более распространена. Пусть задана квадратичная функция (3): , которая является, как было показано ранее, выпуклой функцией с минимумом в точке. Возьмем начальную точку х⁰=(1, 1) (это можно считать начальной локализацией). Зафиксируеми найдем экстремум по координате х₂из уравнения:,,.

Д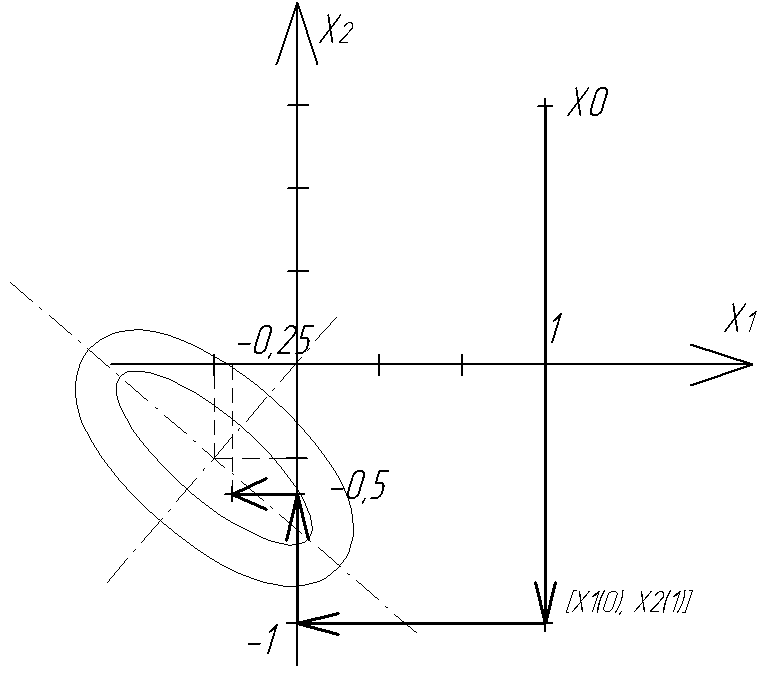алее фиксируеми отыскиваем экстремум по х₁,,,. Как видно за одну итерацию, содержащую два шага, экстремум не найден.

Делаем следующий шаг из точки х₁,,,,. Следующий шаг издает. Закончена вторая итерация. Продолжая вычисления, получим точку, т.е. последовательность сходится к экстремальной точке. Теперь встает вопрос, когда закончить вычисления? Т.к. метод З-Г сходится, то вычисления можно прервать на любой итерации. Обычно задают некоторую малую величину, по координатам илипо значению функции. Вычисления заканчиваются тогда, когда разница между значениями координат (или функции) на текущей и на предыдущей итерациях станет меньше или равна данной величинеили. Метод З-Г достаточно прост, но имеет малую скорость сходимости, т.к. на каждой итерации в общем случае надо делатьnшагов при несепарабельных функциях.