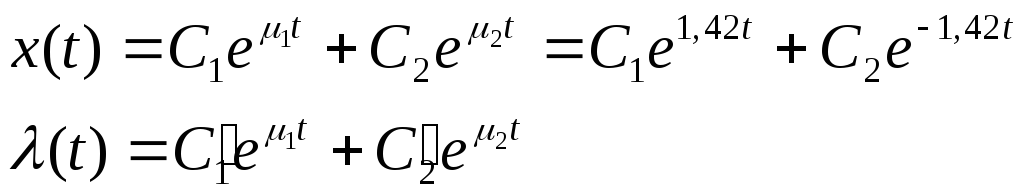- •Управление непрерывными динамическими тп Поиск экстремума функционалов
- •Свойства функций и функционалов
- •Классическое вариационное исчисление Метод Эйлера для определения экстремальных функций без ограничений
- •Решение вариационной задачи на безусловный экстремум при различных заданиях подынтегральной функции в функционале
- •Решение вариационных задач на условный экстремум (метод Эйлера-Лагранжа)
- •Решение задач акр с помощью кви
- •Решение задач акр с помощью метода Эйлера-Лагранжа
- •Решение неклассических задач вариационного исчисления
- •Принцип максимума
- •I. Решение задачи без ограничений на u.
- •II. Решение задачи с ограничениями.
- •Оптимальное по быстродействию управление линейными объектами
- •Теорема об nинтервалах
- •Нелинейные задачи оптимального управления
Решение вариационной задачи на безусловный экстремум при различных заданиях подынтегральной функции в функционале
Пусть задан функционал, зависящий от
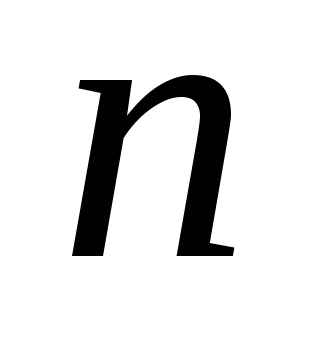 функций
функций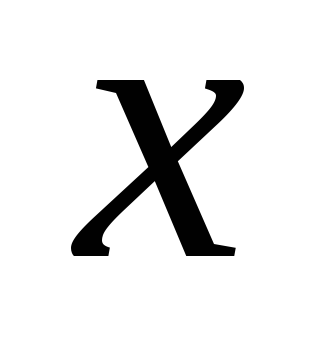 и их первых производных:
и их первых производных:
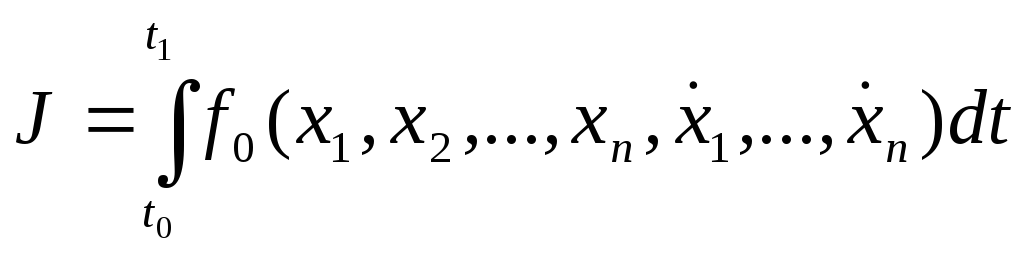 .
.
Для нахождения
экстремальных функций
![]() ,
,![]() составляется
составляется![]() уравнений Эйлера:
уравнений Эйлера:
 .
.
Пусть задан функционал, подынтегральное выражение которого зависит от функции и ее производных, т.е.
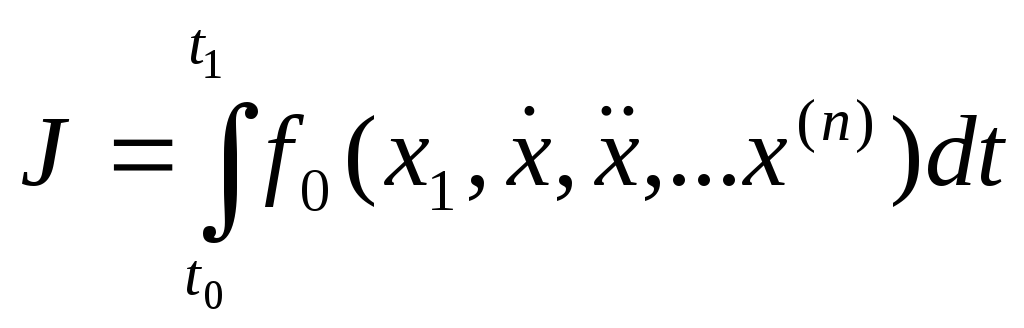 .
.
Решение данного функционала находится из уравнения Эйлера-Пуассона
![]()
Если пределы
интегрирования заданы на полубесконечном
интервале, т.е. требуется, чтобы решение
![]() было устойчмвым и не имело расходящихся
слагаемых, то решением уравнения
Эйлера-Пуассона является функция
было устойчмвым и не имело расходящихся
слагаемых, то решением уравнения
Эйлера-Пуассона является функция
![]() ,
,
![]() .
.
Решение вариационных задач на условный экстремум (метод Эйлера-Лагранжа)
Пусть дан функционал
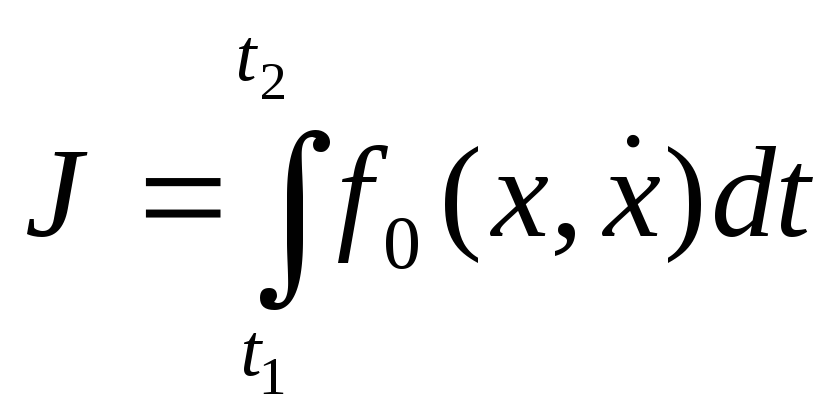 , (1)
, (1)
куда в общем случае
входят и производные переменных
![]() и уравнения связи
и уравнения связи
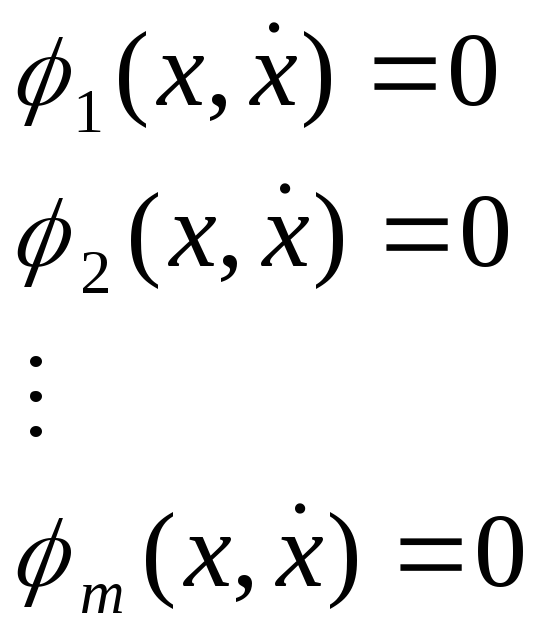 , (2)
, (2)
Требуется найти
функции
![]() доставляющие экстремум функционалу
доставляющие экстремум функционалу![]() .
Это постановка задачи поиска экстремума
с ограничениями в форме равенств. Для
ее решения применяется метод множителей
Лагранжа, с помощью которого исходная
задача на условный экстремум сводится
к задаче на безусловный экстремум. Для
этого вводится новая функция
.
Это постановка задачи поиска экстремума
с ограничениями в форме равенств. Для
ее решения применяется метод множителей
Лагранжа, с помощью которого исходная
задача на условный экстремум сводится
к задаче на безусловный экстремум. Для
этого вводится новая функция
![]() , (3)
, (3)
т.е. новая функция
будет зависеть от переменных системы,
а также от множителей Лагранжа
![]() ,
,![]() ,
зависящих от времени.
,
зависящих от времени.
Для любой новой
функции составляются уравнения Эйлера
по переменным системы
![]() .
Получаемые уравнения будут зависеть
от
.
Получаемые уравнения будут зависеть
от![]() .
Решая совместно уравнения связи и
уравнения Эйлера, находят искомое
решение
.
Решая совместно уравнения связи и
уравнения Эйлера, находят искомое
решение![]() в функции времени. Этот метод поиска
экстремума функции с ограничениями в
виде равенств называется методом
Эйлера-Лагранжа.
в функции времени. Этот метод поиска
экстремума функции с ограничениями в
виде равенств называется методом
Эйлера-Лагранжа.
Решение задач акр с помощью кви
П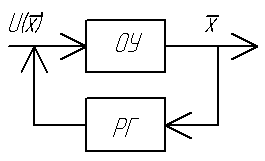 остановка
задачи.Конструирование таких
регуляторов, которые обеспечивают
необходимый вид переходного процесса.
Переходному процессу дается некоторая
интегральная оценка в виде функционала
на полубесконечном интервале, чем
гарантируется устойчивость переходного
процесса.
остановка
задачи.Конструирование таких
регуляторов, которые обеспечивают
необходимый вид переходного процесса.
Переходному процессу дается некоторая
интегральная оценка в виде функционала
на полубесконечном интервале, чем
гарантируется устойчивость переходного
процесса.
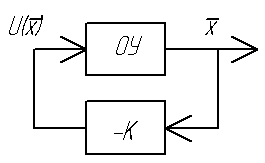
Имеется ОУ
![]() .
Требуется найти такое управление
.
Требуется найти такое управление![]() – уравнение обратной связи или регулятора,
чтобы обеспечивалось устойчивость
системы и заданные показатели качества
переходного процесса.
– уравнение обратной связи или регулятора,
чтобы обеспечивалось устойчивость
системы и заданные показатели качества
переходного процесса.
Задание переходного процесса различными типами функционалов.Переходный процесс можно задавать различными типами интегральных функционалов. Проведем их сравнение.
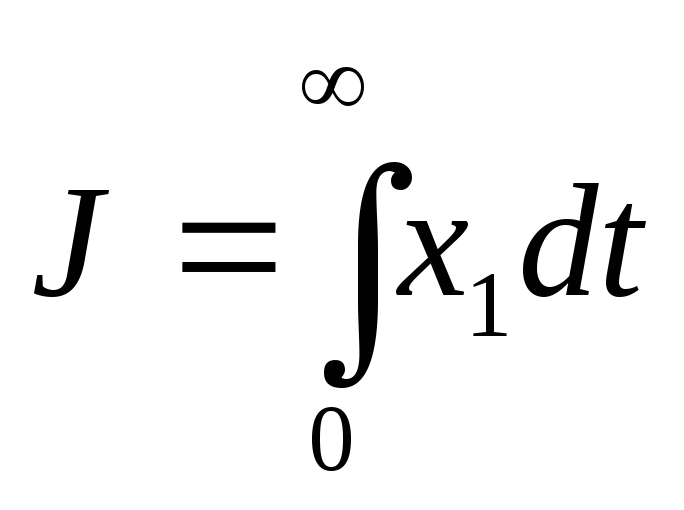 ,
,
 – изменение фазовой переменной в
переходном процессе. Как известно,
интеграл характеризует площадь,
ограниченную подынтегральной функцией.
Например.
– изменение фазовой переменной в
переходном процессе. Как известно,
интеграл характеризует площадь,
ограниченную подынтегральной функцией.
Например.
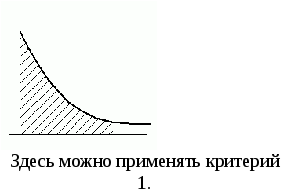

Этот критерий не точно отражает колебательность системы, т.к. отрицательные отклонения компенсируют положительные.
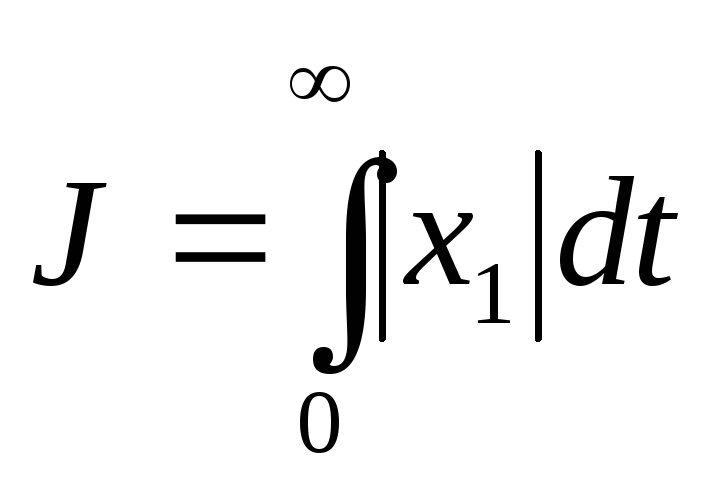
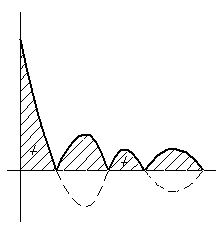 –этот функционал
будет характеризовать колебательность,
однако его недостаток в том, что
подынтегральная функция в нем является
неаналитической.
–этот функционал
будет характеризовать колебательность,
однако его недостаток в том, что
подынтегральная функция в нем является
неаналитической. –довольно удачный
критерий, характеризует колебательность,
причем чем больше отклонения, тем больше
значения квадрата отклонения
–довольно удачный
критерий, характеризует колебательность,
причем чем больше отклонения, тем больше
значения квадрата отклонения
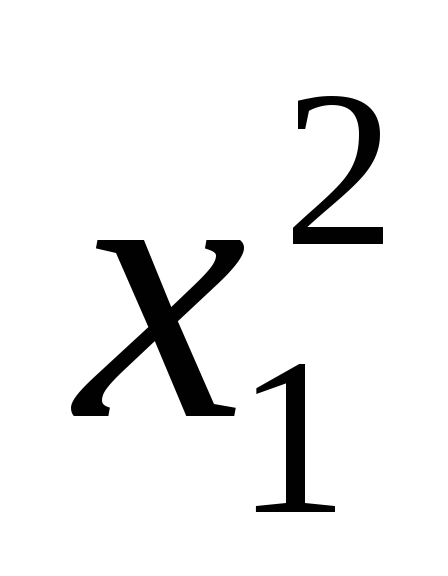 .
Но недостаток данного функционала в
том, что не ограничивается скорость
изменения
.
Но недостаток данного функционала в
том, что не ограничивается скорость
изменения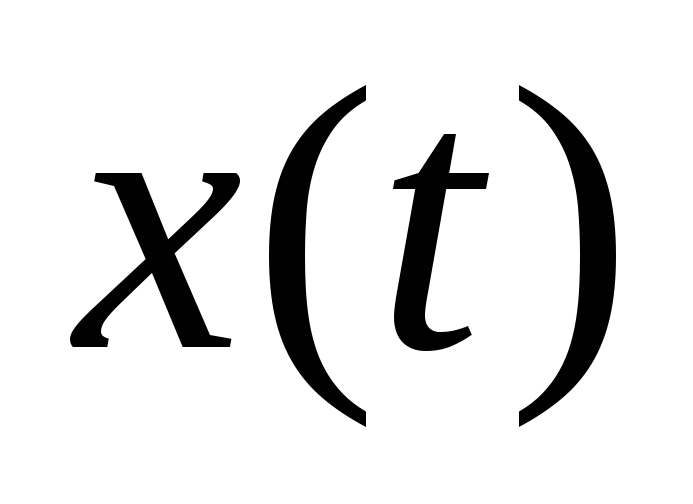 в переходном процессе.
в переходном процессе.
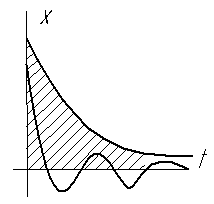
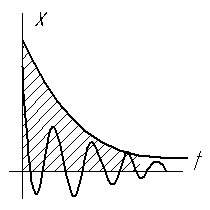
![]() ,
хотя характер переходного процесса
различен.
,
хотя характер переходного процесса
различен.
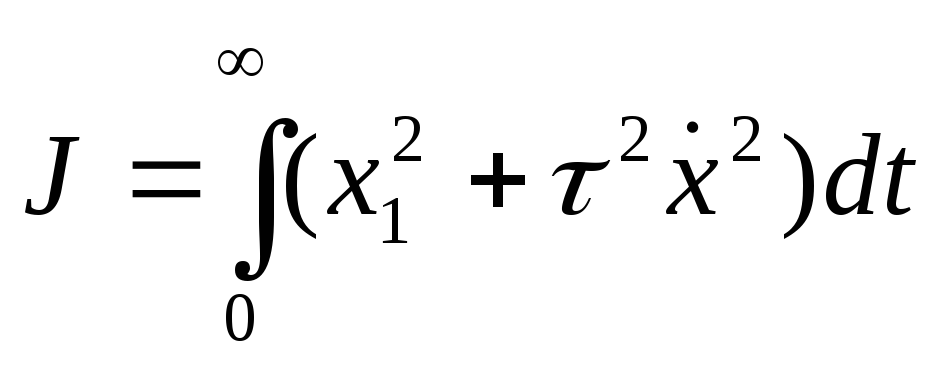 –здесь
–здесь
 – весовой коэффициент, характеризующий
изменение производной
– весовой коэффициент, характеризующий
изменение производной .
Еще его называют коэффициент штрафа.
Если
.
Еще его называют коэффициент штрафа.
Если мало, то налагается малый штраф на
производные, т.е. допустимы большие
значения производной и наоборот.
мало, то налагается малый штраф на
производные, т.е. допустимы большие
значения производной и наоборот.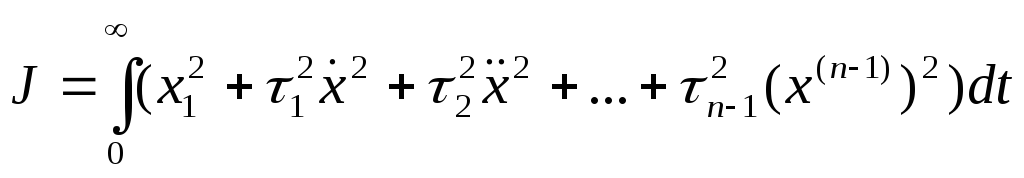 .
Такой критерий называется обобщенным
или критерием Фельдбаума, он характеризует
изменение самой функции и
.
Такой критерий называется обобщенным
или критерием Фельдбаума, он характеризует
изменение самой функции и
 ее производных.
ее производных.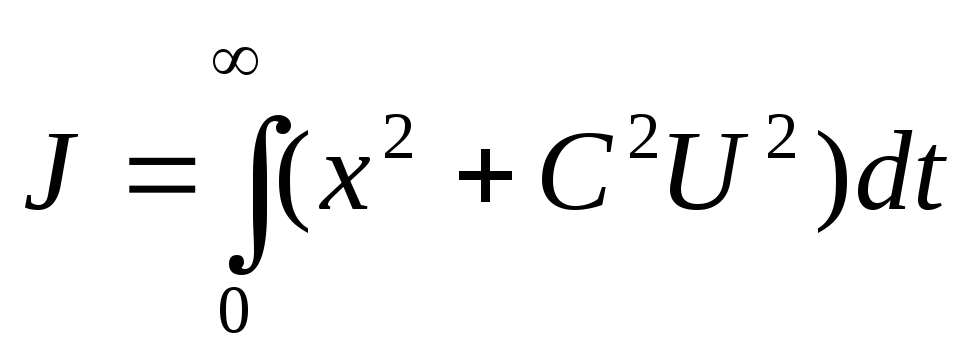 –этот довольно
простой критерий учитывает не только
отклонения
–этот довольно
простой критерий учитывает не только
отклонения
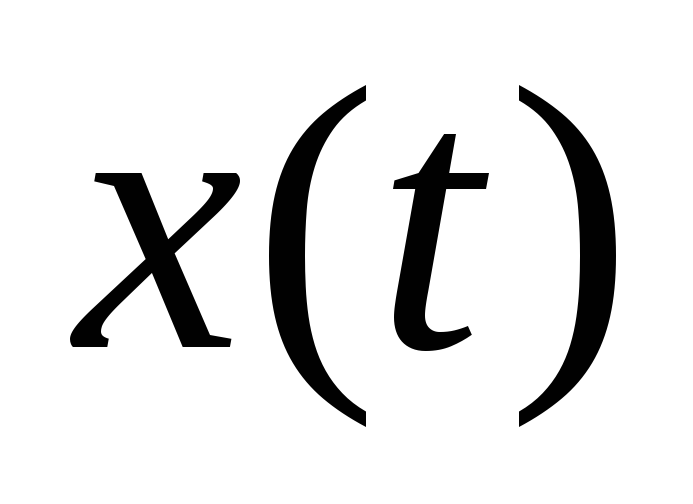 ,
но и поступление энергии в систему.
,
но и поступление энергии в систему.
На практике вид переходного процесса чаще всего задается функционалами 5 и 6.
Рассмотрим шаги процедуры решения задачи АКР.
Задается математическое описание системы
![]() ,
,
учитывающее и объект управления и уравнения различных исполнительных и измерительных устройств.
Задание
 ,
в том числе весовых коэффициентов.
Интеграл берется от 0 до
,
в том числе весовых коэффициентов.
Интеграл берется от 0 до ,
т.е. характеризует устойчивость системы.
,
т.е. характеризует устойчивость системы.Для поставленной задачи решается задача поиска экстремума функционала с ограничениями в виде равенств
![]() или
или
![]()
с помощью метода Эйлера-Лагранжа.
Получают решение
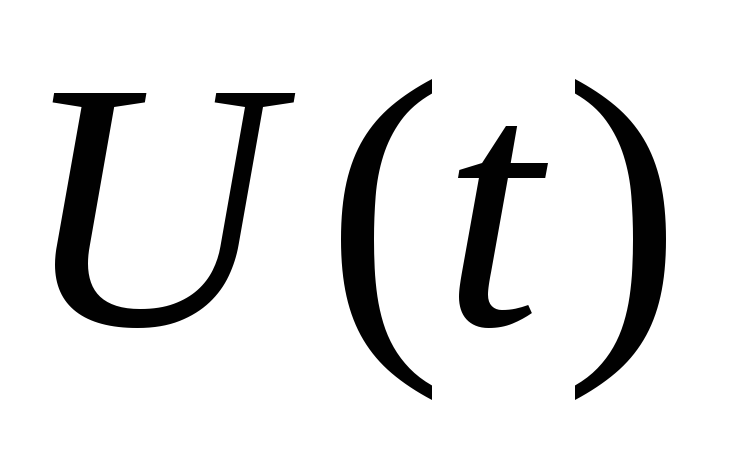 ,
,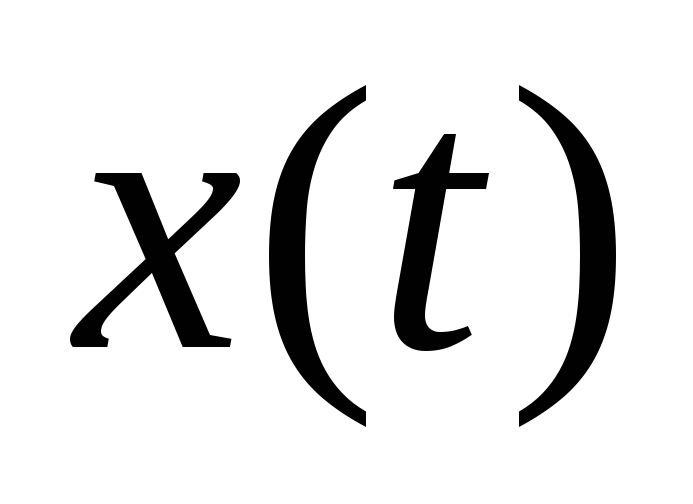 из совместного решения уравнений Эйлера
и уравнений системы.
из совместного решения уравнений Эйлера
и уравнений системы.Исключая время, т.е. записывая
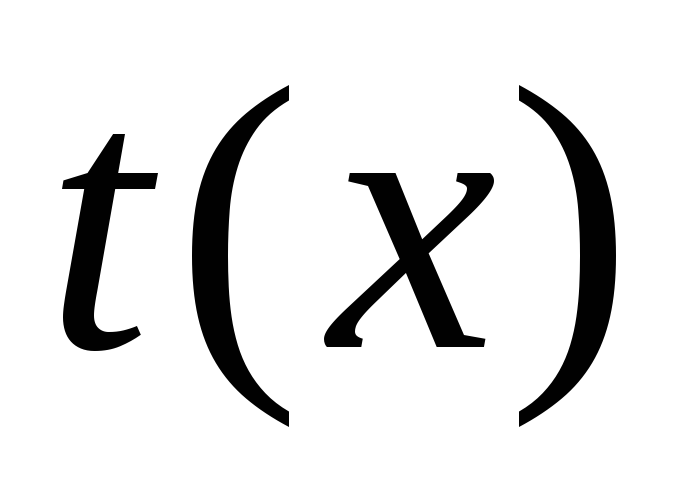 и подставляя
и подставляя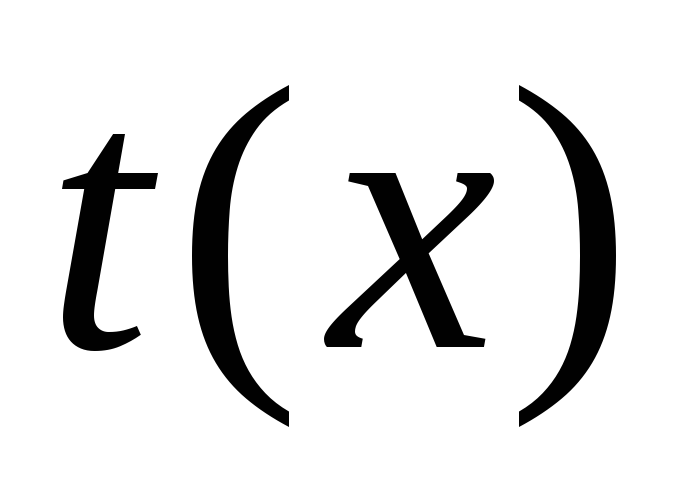 в
в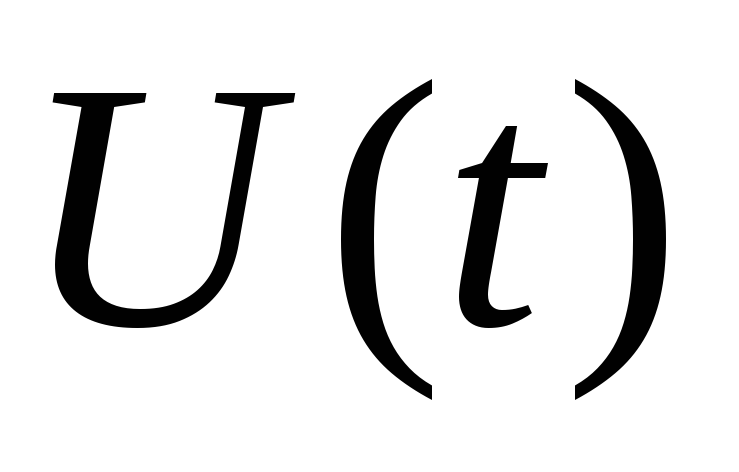 ,
получают уравнение регулятора или, как
говорят, синтезируют систему управления
(замыкают ее).
,
получают уравнение регулятора или, как
говорят, синтезируют систему управления
(замыкают ее).
Пример.
Дано уравнение объекта
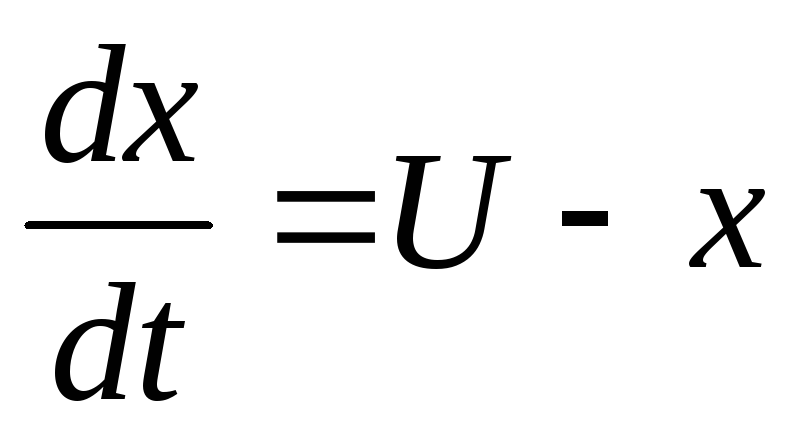 ,
,
и уравнение функционала
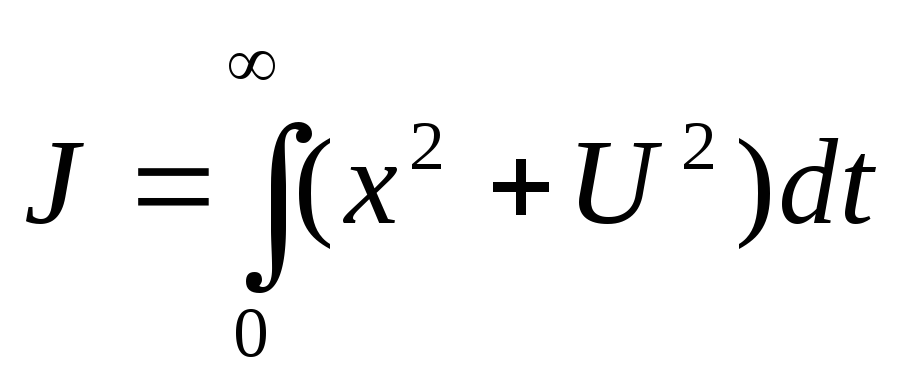 .
.
Требуется найти
![]() ,
переводящее объект из
,
переводящее объект из![]() в точку, соответствующую минимуму
функционала.
в точку, соответствующую минимуму
функционала.
Записываем уравнение Эйлера-Лагранжа:

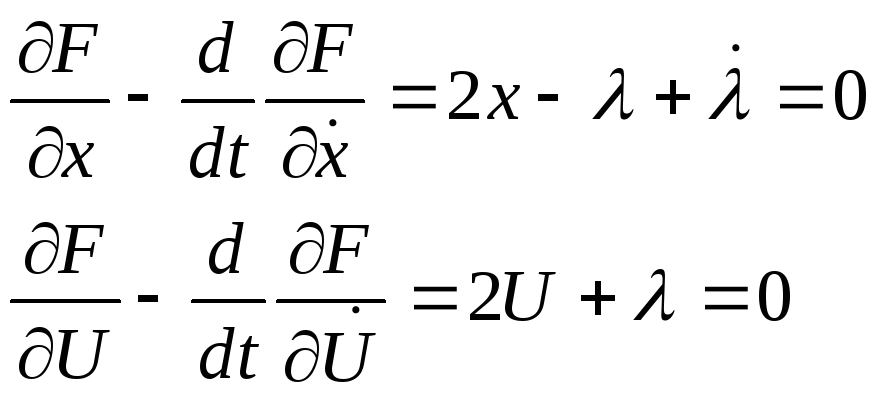 ,
,

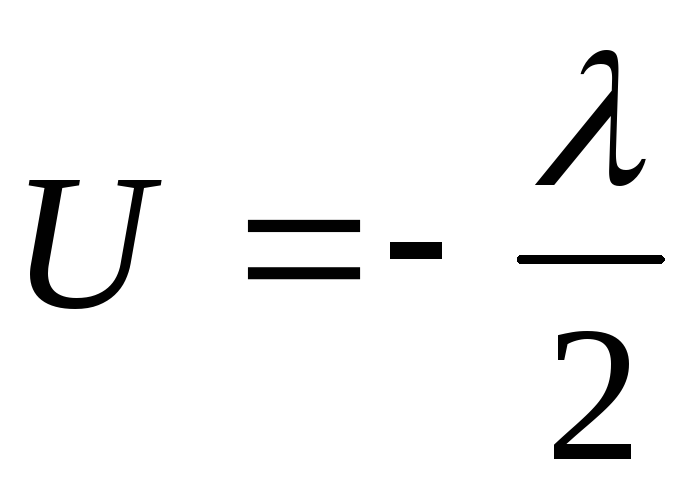 .
.
Нахождение
 и
и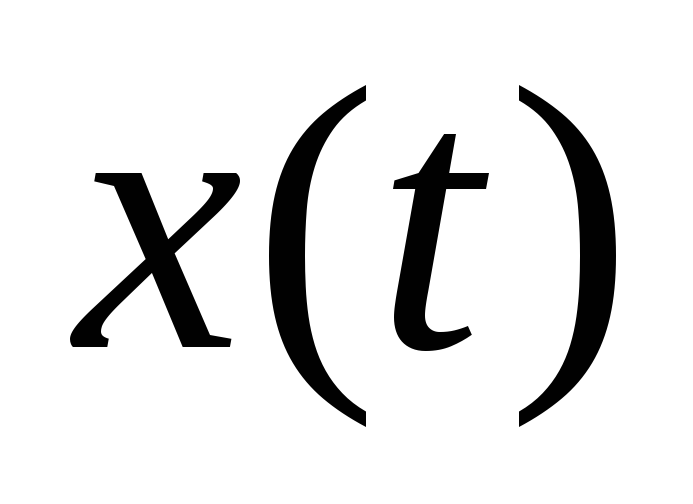 :
: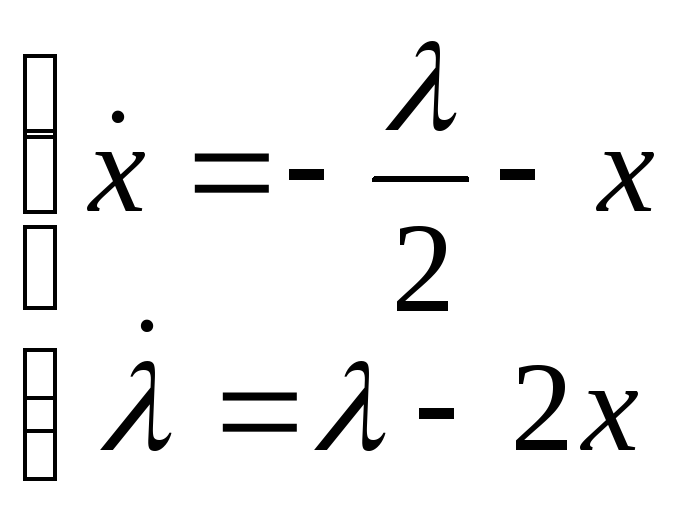
Находится характеристический определитель для последней системы:
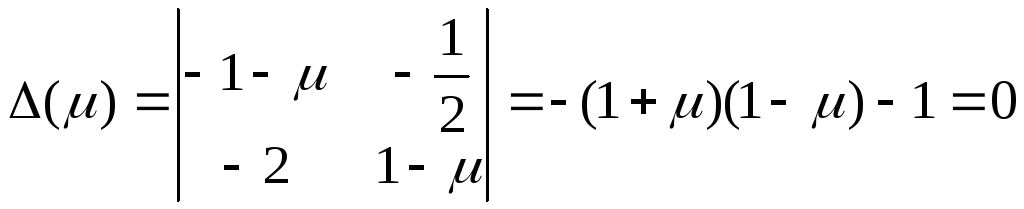
![]()
![]()
Т.к. требуется
устойчивость, то
![]() следует отбросить.
следует отбросить.
Итак
![]() .
.![]() .
.
Исключение времени
![]()
![]()
Д ля
конкретного граничного условия
ля
конкретного граничного условия![]() получим подстановкой в уравнение связи
получим подстановкой в уравнение связи![]() ,
находим
,
находим![]() :
:![]() ,
,
![]()
![]() .
.