Sebery J.Cryptography.An introduction to computer security.1989

Encryption: A message m 2 M is encrypted by random selection of a homophone from Hm, i.e. c = Ek(m) = h 2R Hm (where 2R means that element is chosen randomly and uniformly).

Decryption: Knowing a cryptogram c 2 C, the decryption relies on nding the set Hm to which c belongs { the message is m.

Unicity Distance: If sets of homophones contain single elements only, the cipher becomes a monoalphabetic substitution cipher with j K j= 26! and the unicity distance 27:6. If each set of homophones has exactly v elements

and H = 26 v, then j K j= (26v)! and the unicity distance is N 38:2 v

(v!)26

(note that this approximation does not work very well for small v = 1;2; 3). Cryptanalysis: Uses homophone frequency distributions. If there is enough ciphertext, it is easy to determine the set C. From the language frequency distribution, guesses about ni can be made. The nal stage would involve

enumeration of possible assignments of homophones to messages.

3.1.6 Polyalphabetic Substitution Ciphers

Whereas homophonic substitution ciphers hide the distribution via the use of homomorphisms, polyalphabetic substitution ciphers hide it by making multiple substitutions. Leon Battista Alberti (see [265]) used two discs which were rotated according to the key. In e ect this gave, for a period d, d di erent substitutions. Thus polyalphabetic substitution ciphers apply d di erent permutations

i : Z26 ! Z26 for i = 1; : : : ; d and the message,

m = m1; m2; : : : ; md; md+1; md+2; : : : m2d becomes,

Ek(m) = 1(m1); 2(m2); : : : ; d(md); 1(md+1); : : : ; d(m2d)

Note that if d = 1, we get back the monoalphabetic substitution cipher. We now give a few methods for obtaining polyalphabetic ciphers.

Vigenere cipher

Message Space: M = Z26d { d-letter sequences.

82 3 PRIVATE-KEY CRYPTOSYSTEMS

Cryptanalysis: If the period d is not known, then it can be determined using the Kasiski or index of coincidence methods (see the next Section). Once the period d is known, cryptanalysis reduces to the simultaneous analysis of d independent Caesar ciphers.

Let us consider how the Vigenere cipher can be used. Encipher the message

Cryptanalysis: If the period d is not known, then it can be determined using the Kasiski or index of coincidence methods. Once the period d is known, cryptanalysis reduces to the simultaneous analysis of d independent aÆne ciphers with the known multiplier.

so the same algorithm can be used for encryption and decryption as i = i 1!

In other words, encryption and decryption in the Beauford cipher can be done

using a single algorithm while the Vigenere cipher requires two algorithms: one for encryption and one for decryption.

3.1.7 Cryptanalysis of Polyalphabetic Substitution Ciphers

To break a polyalphabetic substitution cipher, the cryptanalyst must rst determine the period of the cipher. This can be done using two main tools: the Kasiski method, which is named after its inventor Friedrich Kasiski, and the index of coincidence.

The Kasiski method uses repetitions in the ciphertext to give clues to the cryptanalyst about the period. For example, suppose the plaintext TO BE OR NOT TO BE has been enciphered using the key NOW, producing the ciphertext below:

Ek(m) = GCXRC NACPG CXR

Since the characters that are repeated, GCXR, start nine letters apart we conclude that the period is probably 3 or 9.

The index of coincidence (IC), introduced in the 1920s by Friedman [189, 265], measures the variation in the frequencies of the letters in a ciphertext. If the period of the cipher is one (d = 1), that is a simple substitution has been used, there will be considerable variation in the letter frequencies and the IC will be high. As the period increases, the variation is gradually eliminated (due to di usion) and the IC is low (Table 3.2).

Assume that there is an alphabet of n letters uniquely identi able by their positions from the set Zn = f0; 1; : : : ; n 1g. Each character is assigned its corresponding frequency expressed by the probability P (M = m) = pm where m 2 Zn. Note that Pni=0 pi = 1. Following Sinkov [480], we shall derive the IC by rst de ning a measure of roughness, (MR), which gives the variation of the frequencies of individual characters relative to a uniform distribution. So the measure of roughness of the language with Zn and fpi j i = 0; 1; : : : ; n 1g is

For English letters we have

these from a limited number of observed cryptograms.P

Suppose we have seen a ciphertext with N characters. For every character in the ciphertext, let Fi express how many times it has occurred in the ciphertext.

Obviously, P25 Fi = N. Note that Fi can be used to estimate pi as pi Fi=N.

i=0

It is possible to create

N ! = N(N 1) 2 2

pairs of characters out of N observed in the ciphertext. The number of pairs (i; i) containing just the letter i is:

Fi(F2i 1)

The IC is de ned as:

and gives the probability that two letters observed in ciphertext are, in fact,

IC becomes closer and closer to P25 p2 as the number of observed charac-

i=0 i

ters in the ciphertext increases. The IC estimate can be used to compute the corresponding measure of roughness:

MR IC 0:038

Index of Coincidence (an algorithm)

IC1. Collect N ciphertext characters.

IC2. Find the collection F = fFi j i 2 Zng of frequencies for all characters. Note that Pi Fi = N.

IC3. Compute

n F (F 1)

IC = X i i i=0 N(N 1)

For a at distribution of a 26 character alphabet, all letters have the same frequency, 1/26, and the sum of the squares is (1=26)2 26: Hence the MR for a at distribution is 1=26 1=26 = 0. When the MR is 0, corresponding to aat distribution, we say it has in nite period (d = 1). At the other extreme we have period one (d = 1) for simple substitution. English with period one has MR = 0:028. Thus we have:

Thus, while we can get an estimate of d from the ciphertext, it is not exact but statistical in nature and a particular ciphertext might give misleading results.

86 3 PRIVATE-KEY CRYPTOSYSTEMS

d IC

1 0.0660

2 0.0520

3 0.0473

4 0.0450

5 0.0436

6 0.0427

7 0.0420

8 0.0415

9 0.0411

100.0408

110.0405

120.0403

130.0402

140.0400

150.0399

160.0397

170.0396

180.0396

190.0395

200.0394

Table 3.3. Periods and associated indices of coincidence

Table 3.2 gives the index of coincidence for some other languages. For English, the relation between IC and d is given in Table 3.3.

The following attack provides a concrete example of this method. Decrypt the following ciphertext which was produced using the Vigenere cipher:

TSMVM MPPCW CZUGX HPECP REAUE IOBQW PPIMS

Given that the cipher was produced using a Vigenere cipher, we would rst like to determine the period that has been used. The Kasiski method allows us to do that, assuming the repetitions are not coincidental. Examining the trigraphs we nd two occurrences of IYO and LVF. The IYOs are 25 letters apart and the LVFs are 55 apart. The common factors are 1 and 5.

Let us now examine the IC. The frequency count gives us:

a ! 6 g ! 5 1 ! 6 q ! 3 v ! 4 b ! 2 h ! 5 m ! 8 r ! 6 w ! 6 c ! 6 i ! 10 n ! 3 s ! 10 x ! 2

d ! 6 j ! 2 o ! 5 t ! 5 y ! 2 e ! 5 k ! 5 p ! 13 u ! 5 z ! 3

f ! 6

Thus the IC = 0.04066. From the table of ICs (Table 3.3) it appears more likely that 10 alphabets were used than 5, but we will proceed with an assumption of 5. We split the ciphertext into ve sections getting

(a) TMCHRIPFTSODSEGFANGWESITHRHI

from text positions 5i, i = 0; 1; : : : ; 27.

(b) SPZPFOPXSZPDLLHNRODSDMYLPALY

from text positions 5i + 1, i = 0; 1; : : : ; 27.

(c) MPUEABIIQNAPVTIIMSIGMWOVBQDO

from text positions 5i + 2, i = 0; 1; : : : ; 27.

(d) VCGCUQMPPUCKFKZDUKPVCKJFJIGU

from text positions 5i + 3, i = 0; 1; : : : ; 27.

(e) MWXPEWSCKLRTWRSFERHLMPSAIWA

from text positions 5i + 4, i = 0; 1; : : : ; 27.

In Table 3.4, the frequency distribution for each of these ve sections is shown. Each column of Table 3.4 corresponds to the frequency distribution of the section indicated by the text position in the heading. Thus column 4, headed by 5i + 3 corresponds to the fourth section which gave text positions 5i + 3.

It would be best to consider columns 2 and 4 as their IC is 0.06614 which corresponds most closely to English. In the second column of Table 3.4 we see L and P occur frequently, suggesting that they might be A and E respectively. In the fourth column we are more uncertain what initial guess to try for A so we will try the three most frequent values as guesses for A, i.e. U, C, K.

The second section is:

SPZPFOPXSZPDLLHNRODSDMYLPALY

Since P is the most common letter we are going to replace P ! E, Q ! F, : : :

getting:

HEOEUDEMHOESAAWCGDSHSBNAEPAN

88 3 PRIVATE-KEY CRYPTOSYSTEMS

Table 3.4. Frequency distribution for the ve sections of the ciphertext

The fourth section is:

VCGCUQMPPUCKFKZDUKPVCKJFJIGU

Hence replacing U ! A, V ! B, : : : we get:

BIMIAWSVVAIQLQFJAQVBIQPLFOMA,

which we quickly decide is unlikely to be English because of the number of Qs. The other choices for A, from the frequency distribution are C ! A or K ! A. Trying these gives, respectively:

TAEASOKNNSAIDIXBSINTAIHDHGES

CGCEGCFFECAFAJDEAFFCADFDCGE

Of these two the rst looks the most promising so we look at what we have for our ve sections as rows:

. . . . . . . . . . . . . . . . . . . . . . . . . . .

H E O E U D E M H O E S A A W C G D S H S B N A E P A N

. . . . . . . . . . . . . . . . . . . . . . . . . . .

T A E A S O K N N S A I D I X B S I N T A I H D H G E S

. . . . . . . . . . . . . . . . . . . . . . . . . . .

Neither row is part of a sentence so we look down the rst column and decide that since the most common rst word in English is THE we will start by leaving the rst row as it is and replacing M ! E, N ! F, . . . in the third row giving:

T M C H R I P F T S O D S E G F A N G W E S I T H R H I H E O E U D E M H O E S A A W C G D S H S B N A E P A N E H M W S T A A I F S H N L A A E K A Y E O G N T I V G T A E A S O K N N S A I D I X B S I N T A I H D H G E S

. . . . . . . . . . . . . . . . . . . . . . . . . . .

Hence we decide that the plaintext is:

THE TIME HAS COME THE WALRUS SAID TO SPEAK OF MANY THINGS OF SHOES AND SHIPS AND SEALING WAX OF CABBAGES AND KINGS AND WHY THE SEA IS BOILING HOT AND WHETHER PIGS HAVE WINGS.

Looking at the character which gave A in each of the ve alphabets gives us the key ALICE.

3.2 DES Family

This section discusses modern cryptographic algorithms. The discussion starts from the description of Shannon's concept of product ciphers. Later Feistel transformations are studied. The Lucifer algorithm along the Data Encryption Standard (DES) are presented.

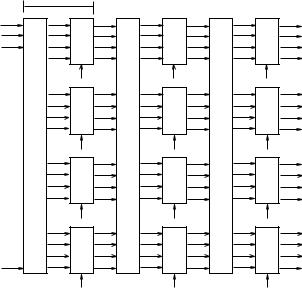
90 3 PRIVATE-KEY CRYPTOSYSTEMS

Fig. 3.5. S-P network

3.2.1 Product Ciphers

Shannon [468] proposed composing di erent kinds of simple and insecure ciphers to create complex and secure cryptosystems. These complex cryptosystems were called product ciphers. Shannon argued that to obtain secure ciphers, the designer had to operate on large message and key spaces and use simple transformations to incorporate confusion and di usion. The concept is illustrated in Figure 3.5. The S-boxes are simple substitution ciphers and they provide confusion because of the secret keys used. Permutation boxes (P-boxes) di use partial cryptograms across the inputs to the next stage. The P-boxes have no secret key. They have a xed topology of input-output connections. The product cipher needs to have a number of iterations or rounds. A single round consists of concatenation of a single P-box with the subsequent layer of S-boxes. The more rounds, the better mixing of partial cryptograms. Consequently the probability distribution of the cryptograms becomes atter. Product ciphers based on substitution and permutation boxes are also known as substitution-permutation networks (S-P networks). S-P networks are expected to have [67]: