
Sebery J.Cryptography.An introduction to computer security.1989
.pdf4.8 Public-Key Encryption Practice |
211 |
using the Chinese Remainder Theorem.
4.8 Public-Key Encryption Practice
Public-key cryptography traditionally is used to provide con dentiality of data via encryption under a standard assumption that the attacker is an outsider. The experience demonstrates that in many applications, the attacker is more likely to be an insider who apart from public encryption, may access decryption algorithm. In the so-called lunch-time or midnight attack, an insider can for some time play with the decryption device asking for messages which correspond to a collection of cryptograms chosen by the attacker. The device is assumed to be tamperproof so the attacker is not able to see the secret key.
4.8.1 Taxonomy of Public-Key Encryption Security
It is reasonable to assume that the computational power of an adversary is polynomially bounded. A public-key cryptosystem can be used to provide the following general security goals:
{One-wayness (OW) { the adversary who sees a cryptogram is not able to compute the corresponding message (plaintext).
{Indistinguishability (IND) { observing a cryptogram, the adversary learns nothing about the plaintext.
{Nonmalleability (NM) { the adversary observing a cryptogram for a message m, cannot derive another cryptogram for a meaningful plaintext m0 related to m.
The goals OW and IND relate to the con dentiality of encrypted messages. The IND goal is, however, much more diÆcult to achieve than the one-wayness. Note that probabilistic encryption presented in Section 4.7 provides indistinguishability (also termed semantic security). Nonmalleability guarantees that any attempt to manipulate the observed cryptogram to obtain a valid cryptogram, will be unsuccessful (with a high probability). For example, the RSA cryptosystem is malleable. The adversary knowing a cryptogram c = me, can for the message m0 = 2m, create the valid cryptogram c0 = c 2e. This allows an adversary to produce valid cryptograms for unknown messages which are smaller or bigger from m (the adversary always wins in electronic bidding).
212 4 PUBLIC-KEY CRYPTOSYSTEMS
The power of a polynomial attacker (with polynomial computing resources) very much depends on his access to the information about the public-key system. The weakest attacker is an outsider who knows the public encryption algorithm together with other public information about the setup of the system. The strongest attacker seems to be an insider who can access the decryption device in regular intervals (lunch-time and midnight attacks). The access to the decryption key is not possible as the decryption device is assumed to be tamperproof.
A decryption oracle is a formalism that mimics an attacker's access to the decryption device. The attacker can experiment with it providing cryptograms and collecting corresponding messages from the oracle (the attacker cannot access the decryption key). In general, the public-key cryptosystem can be subject to the following attacks (ordered in increasing strength):
{Chosen plaintext attack (CPA) { the attacker knows the encryption algorithm and the public elements including the public key (the encryption oracle is publicly accessible).
{Nonadaptive chosen ciphertext attack (CCA1) { the attacker has access to the decryption oracle before he sees a cryptogram that he wishes to manipulate.
{Adaptive chosen ciphertext attack (CCA2) { the attacker has access to the decryption oracle before and after he observes a cryptogram c that he wishes to manipulate (assuming that he is not allowed to query the oracle about the cryptogram c).
The security level that a public-key system achieves can be speci ed by the pair: (goal, attack) where goal can be either OW, or IND, or NM, and attack can be either CPA, or CCA1, or CCA2. For example, the level (NM, CPA) assigned to a public-key system says that the system is nonmalleable under the chosen plaintext attack. There are two sequences of trivial implications:
(NM, CCA2) ) (NM, CCA1) ) (NM, CPA)
(IND, CCA2) ) (IND, CCA1) ) (IND, CPA)
which are true because the amount of information available to the attacker in CPA, CCA1 and CCA2 grows. Figure 4.3 shows the interrelation among di erent security notions [22]. Consequently, we can identify the hierarchy of security levels. The top level is occupied by (NM, CCA2) and (IND,CCA2). The bottom level contains (IND,CPA) only as the weakest level of security. If we are

4.8 Public-Key Encryption Practice |
213 |
(NM, CCA2)  (NM, CCA1)
(NM, CCA1)  (NM, CPA)
(NM, CPA)
(IND, CCA2)  (IND, CCA1)
(IND, CCA1)  (IND, CPA)
(IND, CPA)
Fig. 4.3. Relations among security notions
after the strongest security level, its is enough to prove that our cryptosystem attains the (IND,CCA2) level of security.
4.8.2 Generic OAEP Public-Key Cryptosystem
Most public-key encryption systems exhibit strong algebraic properties which may be exploited by an attacker. For instance, the RSA cryptosystem has a multiplicative property, which can be used by an adversary to produce valid cryptograms from a pair of cryptograms created by the sender. Suppose that the attacker knows c1 and c2, then they are sure that the ciphertext
is a valid one for the message m1 m2 , although they do not know actual values of m1 and m2. This could be a security problem in electronic bidding since you can create a valid cryptogram that encrypts a larger (or smaller) message.
Clearly, it would be desirable to \destroy" relations among messages and their cryptograms by the introduction of a redundancy. Bellare and Rogaway [23] introduced the concept of optimal asymmetric encryption padding or OAEP for short. OAEP is a probabilistic encoding of messages before they are encrypted by a public-key cryptosystem. The construction uses random oracles.
A random oracle H : n ! ` is a function, which, for an argument x 2 n, returns a value y which is selected randomly, uniformly and independently from`. Random oracle is a theoretical concept that is very useful because its well formulated probabilistic properties allow to derive conclusions about security. The conclusions are said to be valid in the random oracle (RO) model.
The downside of this approach is that the security conclusions obtained for the RO model may not hold (this happens when the hash function exhibits properties not expected to exist in the random oracle). The following components are used:
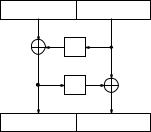
214 4 PUBLIC-KEY CRYPTOSYSTEMS
n-bit |
l - bit |
m |
r |
|
G |
|
H |
s |
t |
n-bit |
l - bit |
Fig. 4.4. Optimal asymmetric encryption padding
{An instance of a public-key cryptosystem with public encryption algorithm
E and secret decryption algorithm D = E 1 where E : n+` ! n+`. It is assumed that E is a one-way permutation so a polynomially-bounded attacker cannot reverse it.
{Two random oracles G : ` ! n and H : n ! `.
Encryption of a message m 2 n proceeds as follows (Figure 4.4):
1.Generate a random value r 2R `.
2.Calculate
s = m G(r) and t = r H(s):
3. Compute the corresponding cryptogram c = E(s; t) 2 n+`:
Decryption rst recovers the pair (s; t) = E 1(c), the random value r = t H(s) and the message m = s G(r). The security of the system meets (IND,CPA).
Note that OAEP cryptosystem is no longer deterministic. For the same message, the system generates di erent cryptograms with a high probability. It is expected that cryptograms of two or more messages are not \related" even if the messages are related. OAEP breaks relations among cryptograms by using the Feistel permutation with oracles G and H. Any message is rst masked by adding G(r) to it. As ri is likely to be di erent for each message, then a sequence of mi G(ri) are likely to be a sequence of unrelated numbers. The second oracle H masks r. Both masked strings s and t are concatenated and encrypted.
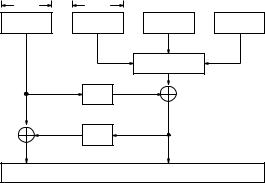
4.8 Public-Key Encryption Practice |
215 |
hLen |
hLen |
seed |
pHash |
PS |
M |
|
|
DB |
|
|
MGF |
|
|
|
MGF |
|
|
|
maskedSeed |
|
maskedDB |
|
|
EM |
|
Fig. 4.5. PKCS#1 version 2.1 |
|
||
4.8.3 RSA Encryption Standard
RSA Security introduced their public-key encryption standard known as PKCS#1. The early version 1.5 was shown to be subject to the CCA2 attack [43]. We describe the version 2.1, which can be found in http://www.rsasecurity.com/ rsalabs/pkcs. This version is also called PKCS-OAEP and is recommended for new applications.
The message M to be encrypted is rst encoded using the function EME- OAEP-ENCODE(M,P,emLen) where P indicates encoding parameters specifying the choice of hashing algorithms (random oracles) and emLen gives the requested length of encoded message (EM) in octets. The encoding procedure is illustrated in Figure 4.5. The input consists of four strings: seed, pHash, PS and M. Both seed and pHash are hLen octets long. The message can be at most emLen-1-2hLen octets long. The string seed is randomly chosen. pHash=Hash(P) is a string obtained from transforming P by the chosen Hash function. PS consists of emLen-mLen-2hLen-1 zero octets. The encoding
EME-OAEP-ENCODE(M,P,emLen) takes the following steps:
1.Concatenate strings pHash, PS and M and form the string DB in the form
DB=(pHashk PS k 01 k M):
2.Compute
maskedDB = DB MGF(seed,emLen-hLen);
where MGF() is the mask generation function (random oracle).
216 4 PUBLIC-KEY CRYPTOSYSTEMS
3. Calculate
maskedSeed = seed MGF(maskedDB,hLen):
4. Output EM=(maskedSeed,maskedDB).
The encryption runs through the following steps:
1.Encode the message M by invoking the function EM=EME-OAEP-ENCODE(M, P,emLen).
2.Convert the message EM into an integer representation, i.e. m=OS2IP(EM).
3.Apply the RSA encryption primitive or c=RSAEP((N,K),m) where N is the modulus and K the public key.
4.Convert the cryptogram c into its octet equivalent C and output it.
The decryption reverses the operations and rst the encoded message EM is recovered. The decoding procedure allows to verify the correctness of the cryptogram when
{The recovered string DB0 does not contain the string PS of zeros separated by the 01 octet.
{The string pHash0 which is a part of DB0 is not equal to the pHash determined by the encoding parameters P.
PKCS-OAEP is a variant of the generic OAEP public-key encryption and its security is believed to be (IND,CCA2) assuming the RO model (if MGF are replaced by random oracles).
4.8.4 Extended ElGamal Cryptosystem
Cramer and Shoup [115] designed a cryptosystem whose security is based on the presumed diÆculty of the DiÆe-Hellman decision problem.
Name: DiÆe-Hellman decision problem
Instance: Given a group G of large prime order q. Consider the following two distributions:
{ the distribution R of random quadruples (g1; g2; u1; u2) 2 G4
{ the distribution D of quadruples (g1; g2; u1; u2) 2 G4 where g1; g2 are random and u1 = g1r and u2 = g2r for a random r 2 Zq
Question: Given a quadruple coming from unknown distribution (either R or D). Does the quadruple belong to R or D?

4.8 Public-Key Encryption Practice |
217 |
The cryptosystem is interesting as it allows to identify cryptograms which have not been created according to the encryption algorithm. Moreover, the identi cation procedure can be skipped and then the system becomes the original ElGamal.
Extended ElGamal cryptosystem
Problems Used: DiÆe-Hellman decision problem.
Given q for prime q and a hash function H : 3 q chosen from the
Z Zq ! Z
family of universal one-way hash functions.
Message Space: M = Zq . Cryptogram Space: C = Zq4 .
Key generation: Random nonzero elements g1; g2; x1; x2; y1; y2; z 2R Zq are chosen, The following elements are computed:
c = g1x1 g2x2 ; d = g1y1 g2y2 ; and h = g1z:
Public Key: (g1; g2; c; d; h; H). Secret Key: (x1; x2; y1; y2; z).
Encryption: Given a message m 2 Zq, perform the following steps: 1. Choose random r 2R Zq.
2. Compute
u1 = g1r u2 = g2r e = hrm = H(u1; u2; e) v = crdr :
The cryptogram c = (u1; u2; e; v).
Decryption: Given a cryptogram c = (u1; u2; e; v), do the following:
1.Compute = H(u1; u2; e).
2.Check whether
x1+y1 x2+y2 ?
u1 u2 = v:
If the equation does not hold, reject the cryptogram otherwise continue
and output the message m = e u1 z:
Note that the decryption can be done by the original ElGamal system from the pair (u1; e). The whole cryptogram is used to verify its validity. The system is provably secure against CCA2 attack or more precisely meets (IND, CCA2) and using the equivalence from Figure 4.3 satis es (NM, CCA2).

218 4 PUBLIC-KEY CRYPTOSYSTEMS
4.9 Problems and Exercises
1.Name main components of the public-key cryptosystem and formulate security requirements. Discuss the usage of the system for secrecy and authenticity.
2.Given a modulus '(N ) and a public key e, write a C program that calculates a secret key d for the RSA system. Assume that both '(N) and e are long integers.
3.Assume that p = 467 and q = 479. Calculate the secret key in the RSA system, knowing
that the public key is equal to e = 73443.
4. Suppose you want to design an RSA system in which the modulus N = p1 p2 p3 (pi is prime for i = 1; 2; 3). Is it possible? If so, what is the main di erence between this modi cation and the original RSA system? Derive necessary expressions for encryption, decryption and keys.
5.Given a Rabin scheme for p = 179 and q = 191 with the decryption based on the Williams modi cation. Compute the deciphering key. What are cryptograms for two messages M1 = 33001 and M2 = 18344?
6.Write a primality testing algorithm that incorporates both the test based on Fermat's Little Theorem (see Equation (4.13)) and the Miller-Rabin test.
7.Find all primes from the interval (45700, 45750) using the Miller-Rabin test.
8.Implement the sieve of Eratosthenes as a C language program.
9.Suppose that you have an eÆcient probabilistic algorithm A which computes square roots
(modulo N). More precisely, the algorithm takes an integer x and returns a single integer which is a square root px mod N. Show how the algorithm can be applied to factor integers.
10.Use the quadratic sieve algorithm to factor N = 29591. First do the factorization by hand. Next implement the algorithm in C (or other high level programming language) assuming that N is a long integer.
11.Apply the iteration attack to recreate the original message for six di erent pairs (cryptogram, public key) while the RSA system uses the modulus N = 2773. The pairs are:
(a)c = 1561, e = 573;
(b)c = 1931, e = 861;
(c)c = 2701, e = 983;
(d)c = 67, e = 1013;
(e)c = 178, e = 1579;
(f)c = 2233, e = 791.
12.Design the Merkle-Hellman system which encrypts 7-bit messages. Suppose that w =
(!1; : : : ; !7) = (2, 3, 6, 12, 24, 49, 100), q is the smallest integer which is bigger than
P7 !i and r = 119. What is the cryptogram for the message M = 1011011? Show the
i=1
deciphering process.
13. Consider the easy knapsack vector w = (1, 2, 4, 8, 16, 32, 64, 128, 256, 512). Produce the public key using four iterations de ned by the following pairs (q1; r1), (q2; r2), (q3; r3), (q4; r4). Choose primes qi; i = 1; 2; 3; 4, as small as possible. Accept (r1; r2; r3; r4) = (233, 671, 322, 157).
4.9 Problems and Exercises |
219 |
14.Given an ElGamal cryptosystem with the modulus q = 1283 and g = 653. Let the receiver choose k = 977. Compute the public key and a cryptogram for the message m = 751.
15.The ElGamal system works under the assumption that the sender always selects her secret exponent s randomly and independently for each single message. Show how can the security of the system be compromised when the sender has generated two cryptograms (for two di erent messages) using the same secret s.
16.It is highly recommended for the modulus q to be selected in such a way that q 1 has at least one large factor. Formulate an argument and derive an algorithm which eÆciently
solves any instance of the discrete logarithm whenever q 1 has small factors only. Hint: It is requested to calculate a knowing ga mod q when q 1 = p1 pn. Observe that a can be represented by a vector (a1; : : : an) where ai a mod pi. The component ai can be readily recovered by computing (ga)ei mod q where ei is an integer ei 0 mod pj (i 6= j) and ei 1 mod pi.
17.Suppose that q is a Mersenne number so q 1 is prime. Implement the ElGamal system when q = 213 and q 1 = 8191. Do all computations in GF(213) using the modulus p(x) = x13 + x11 + x8 + x4 + 1 (p(x) is an irreducible polynomial over GF(2)). Write C
programs for addition and multiplication.
18.Assume an elliptic curve E11(2; 5) with points whose coordinates P = (x; y) satisfy the following congruence y2 x3 +2x+5 mod 11. Given two points P = (3; 4) and Q = (8; 7). What are the points P + Q, P + P and Q + Q?
19.Let our elliptic curve RSA system apply the group EN (0; b) where N is product of two suitable primes p and q. Decrypt the following cryptograms:
{c = (20060; 21121) for p = 257 and q = 131 and the decrypting key d = 4163,
{c = (1649684061; 291029961) for p = 65537, q = 65543 and decrypting key d = 354897809.
What are the encrypting keys in the two cases?
20.Implement the RSA encryption on an elliptic curve EN (a; 0) using an accessible multiprecision arithmetic system such as MAPLE.
21.Consider the ElGamal cryptosystem on an elliptic curve Ep(0; b0. Assume that p = 233, a point P on the curve is P = (135; 211), the secret key is a multiplier k = 176, and the public key is kP = (107; 127). Encrypt the following messages:
{m = (23; 223) for a secret multiplier s = 97
{m = (120; 37) for a secret multiplier s = 200
Decrypt the following cryptograms:
{c = (R; cx; cy) = ((26; 34); 76; 13)
{c = (R; cx; cy) = ((26; 199); 123; 118)
22.Design an instance of the GM encryption for p = 101, q = 103, u = 5646.
23.The BG probabilistic encryption uses BBS pseudorandom bit generator. Use an instance of the BBS generator for p = 7 and q = 11 to construct the BG encryption. Make necessary assumption. Show encryption and decryption processes.
