Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КР№3 НАША ПО МАТЕМАТИКЕ

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Получили знакочередующийся ряд. Третий член по модулю меньше заданной точности. Значит, достаточно взять два слагае-

1/4 sin x
мых:		dx 0,25000	0,00087 0,24913 .
	x
0
3. Интегрирование			дифференциальных	уравнений
с помощью рядов

Многие дифференциальные уравнения не приводятся к квадратурам, а их решения не выражаются в элементарных функциях. Решения некоторых из этих уравнений могут быть представлены в виде степенных рядов, сходящихся в определенных интервалах. В таких случаях ряд, являющийся решением дифференциального уравнения, можно найти или способом неопределенных коэффициентов, или способом, основанным на применении ряда Тейлора.

Пример 5. Найти в виде степенного ряда решение диффе-

ренциального уравнения y	xy 0 , удовлетворяющее началь-
ным условиям y(0)=1, y (0)	0 .

Решение. Первый способ. Применим метод неопределенных

коэффициентов. Записываем искомое решение

в виде ряда

y C

x 2

x 3

x 4

x 5 ... .

Находим произ-

водные:

x 2

x 3

x 4

...,

2C2

2 3C3 x 3

4C4 x 2

5C5 x 3

6C6 x 4 ... .

Подставляя y и y в данное уравнение, получаем:

2C 2	2 3C 3 x	3 4C 4 x 2 4 5C 5 x 3	5 6C 6 x 4 ...
				.
C 0 x	C1 x 2	C 2 x 3 C 3 x 4 C 4 x 5	C 5 x 6	C 6 x 7 ... .

Приравняв коэффициенты при одинаковых степенях x в обеих частях последнего уравнения, получим систему:

2C2		0,
2	3C3	C0 ,
3	4C4	C1 ,
4	5C5	C2 ,
5	6C6	C3 ,
6	7C7	C4 ,
.......... .......
Используя начальные условия,		из выражений для y и y находим:
y(0) 1 C0 , C0 1, y (0)	0	C1, C1 0 . Решая систему, полу-
		21

чаем

C 2

C 3

C 4

C 5

0, C 6

C 7

0, ... .

2 3

2 3 5 6

Таким образом, искомое решение представляется следую-

щим

рядом:

x 3

x 6

... . Этот ряд сходится

2 3

2 3 5 6

при всех значениях x.

Второй способ. Применим для исходного уравнения метод

последовательных дифференцирований.

Решение

y(x)

ищем в

виде

y(x)

y(0)

y (0)

y(n) (0)

В соответствии с начальными условиями

y(0)

1, y (0)

0 .

Подставляя

уравнение

0, y

получим

y (0)

0 1

0 ;

y(0) 0 . Для получения значений остальных производных будем последовательно дифференцировать исходное уравнение:

y	y xy , y(4)	y y xy		2 y xy ,
y(5)	3y xy , , y(n) (n		2).y(n	3) xy(n	2) ,
Отсюда	получим	y(n) (0)	n 2y(n	3) (0) .	Тогда при

n 3,4,5, имеем:

y(0) 1, y(4) (0) 0, y(5) (0) 0, y(6) (0) 4, y(7) (0) 0, y(8) (0) 0, y(9) (0) 4 7 .

Подставляя найденные значения в степенной ряд для y(x) , получим

y	1	1		x	3	4	x	6		4 7	x	9
		3!				6!				9!

1	x3				x6					x9			.
	2 3		2 3 5 6						2 3 5 6 8 9

1.7. Ряд Фурье функции, заданной на отрезке длиной 2

1. Пусть функция f(x) определена и интегрируема на отрезке [– , ]. Рядом Фурье функции f(x) называется ряд

a0	(an cos nx bn sin nx) ,	(1.16)
2
	n 1

где

1	1
a0	f (x)dx, an	f (x) cos nxdx,

		(1.17)
1
bn	f (x) sin nxdx, n	1,2,3,...

Числа a0 , an , bn называются коэффициентами Фурье функ-

ции f(x).

Теорема 7. Если функция f(x) кусочно-гладкая на отрезке [– , ], т.е. f(x) и ее производная f (x) – непрерывны на отрезке [– , ] или имеют на нем конечное число точек разрыва первого рода, то ряд Фурье функции f(x) сходится в каждой точке отрезка [– , ]. При этом сумма S(x), x [– , ], ряда Фурье (1.16) равна

f (x),

если

точка

непрерывности ;

S (x)

( f (x

f (x

0)), если x

точка разрыва f(x);

( f (x

f (x

0)),

если x

или x .

Здесь f (x0 0)

lim

f (x), f (x0

lim

f (x) .

Сумма S(x) ряда Фурье (1.16) определена для x

(– ,+ ) и

является 2 – периодической функцией.

Пример 1. Разложить функцию f(x)=ex в ряд Фурье в интер-

вале (–

). Построить график суммы ряда.

Решение. Вычислим коэффициенты Фурье функции по фор-

мулам (1.17), учитывая, что

e x sin

xdx

sin

cos

e x

e x cos

xdx

cos

sin

e x

Имеем:

e x dx

sh ;

e x cos nxdx

cos nx

n sin nx

e x

n 2

(

1) n

cos

e cos

(e e

)

n 2

2sh

(

1) n

;

n 2

e x

1 sin nx

n cos nx

sin nxdx

n 2

(e cos

cos n)

1 (

1) n

1 n

n 2

2sh

(

1) n

1 n

n 2

e x	1 (		n)
	1 (		n)

		n 2	1
		n 2	1

e )

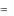
Поскольку функция ex и ее производная непрерывны на отрезке [– , ], то по теореме 7 ряд Фурье этой функции сходится к самой функции ex на интервале (– , ):

(

1)n

(cos nx

n sin x),

1 n2

а в точках x=

сумма ряда равна

e )

. График

суммы ряда изображен на рис. 1.1 (пунктиром – график самой функции ex вне отрезка [– , ]).



-3	- 0	2 3 4	5	x

Рис. 1.1

2. Если f(x) – четная функция на отрезке [– , ], то ее коэффициенты Фурье находятся по формулам

bn 0, a0	2	f (x)dx, an				2	f (x) cos nxdx, n 1,2,... ,	(1.18)


		0					0
а ряд Фурье имеет вид:				a0		an cos nx . Если f(x) – нечетная
а ряд Фурье имеет вид:				2		an cos nx . Если f(x) – нечетная
				2	n	1
					n	1
функция на отрезке [–			, ], то
a0	0, an		0, bn		2		f (x) sin nxdx, n 1,2,... ,	(1.19)
						0


					24

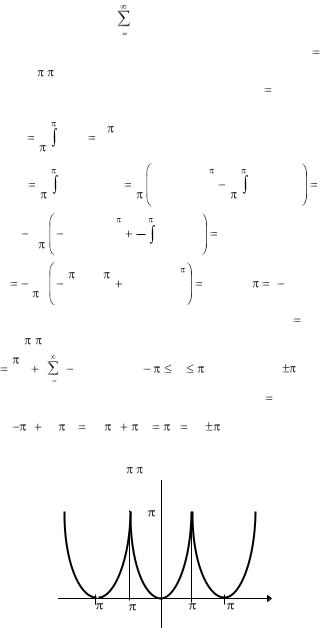
а ряд Фурье имеет вид:					bn sin nx .
				n	1
Пример 2. Разложить в ряд Фурье функцию						f (x)	x 2 на
отрезке [– ,	]. Построить график суммы ряда.
Решение. Поскольку функция четная, то bn						0; a0 , an	нахо-
дим по формулам (1.18), применяя интегрирование по частям:
2		x 2 dx	2	2
a0					,
a0	0		3		,
			3

an	2	x 2 cos nxdx


		0
=	4		x cos nx
	4		x cos nx

	n		n	0
	n		n

2 x 2 sin nx			2	x sin nxdx
	n	0		x sin nxdx
	n			0
				0

1 cos nxdx n 0

						4				cos n				1			sin nx				4	cos n		(	1)	n	4	.
						n					n			n 2			sin nx		0		n 2	cos n		(	1)		n 2	.
						n					n			n 2					0		n 2						n 2
Согласно теореме 7, ряд Фурье данной функции																								f (x)			x 2 на от-
резке [–					,	] сходится к самой функции x2:
			2								n cos nx
x		2				4 (		1)			n cos nx				,			x			(в точках x=					сумма ря-
x				3		4 (		1)					n2		,			x			(в точках x=					сумма ря-
				3			n 1						n2
да			совпадает						со				значением					функции					f (x)	x 2 ,			так как
	1		( f (		)	f (		))				1	( 2			2 )		2		f ( ) .			На рис.		1.2 изобра-
2			( f (		)	f (		))			2		( 2			2 )				f ( ) .			На рис.		1.2 изобра-
2											2

жен график суммы данного ряда (пунктиром – график самой функции x2 вне отрезка [– , ].

-2

- 0

Рис. 1.2

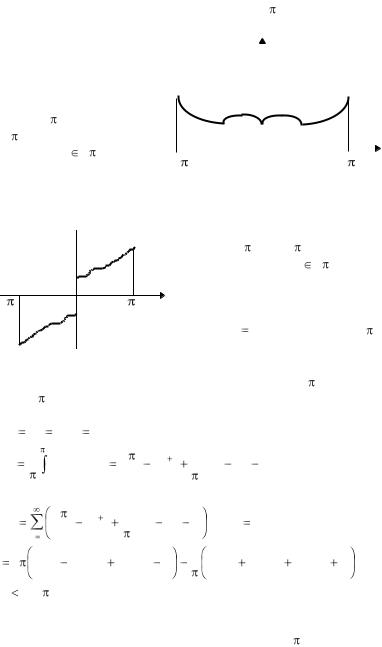
3. Если функция f(x) задана на отрезке [0, ] и удовлетворяет на нем условиям теоремы 7, то ее можно разложить в ряды Фурье

различным образом, на-						y
различным образом, на-						y
пример, как по косину-
сам, так и по синусам.
В		первом		случае
продолжают f(x) с интер-
вала	(0,	)	на	интервал
(– ,0)	четным			образом:
f(x)=f(–x),		x	(–	,0) (рис.
						0	x
					-
1.3), а коэффициенты Фурье					-
1.3), а коэффициенты Фурье
вычисляют			по	формулам		Рис. 1.3
(1.18);						Рис. 1.3
(1.18);

Рис. 1.4

вал (– ,0) нечетным образом формулам (1.19):

во втором – продолжают f(x) с интервала (0, ) на (– ,0) нечетным образом: f(x)=–f(x), x (– ,0) (рис. 1.4), а коэффициенты находят по формулам (1.19).

Пример3. Разложить функцию f (x) x 2 на интервале (0, )

в ряд Фурье по синусам. Решение. Продолжим функ-

цию x2 с интервала (0, ) на интер- и вычисляем коэффициенты по

a0	an		0, (n			1,2,...),
b	2	x2 sin nxdx						2		(		1)n 1	4		(( 1)n	1) .
b		x2 sin nxdx								(		1)n 1			(( 1)n	1) .
n									n				n3
	0								n				n3
	0
Тогда
x2		2		(		1)n 1	4				(( 1)n		1)	sin nx
x2	n 1		n	(		1)n 1			n3		(( 1)n		1)	sin nx
	n 1		n						n3
2	sin x				sin 2x		sin 3x					...	8	sin x		sin 3x		sin 5x	... ,

						2	3								13	33	53
						2	3								13	33	53

0 x .

(Сравните разложение этой же функции x2 в ряд по косинусам, полученное в примере 2).

4. Если функция f(x) задана на отрезке [a,a+2 ], то ее коэффициенты Фурье вычисляются по формулам:

	1 a	2		1 a	2
a0			f (x)dx, an		f (x) cos nxdx,

		a			a
bn	1 a	2	f (x) sin nxdx, n		1,2,... .

1.8. Ряд Фурье функции, заданной на отрезке длиной 2l

Пусть функция f(x) определена и интегрируема на отрезке [–l,l]. Рядом Фурье функции f(x) называется ряд

	a0	an cos	nx	bn sin	nx	,
2		an cos	l	bn sin	l	,
2		n 1	l		l
		n 1
где

1 l

f (x )dx, a

1 l

f (x ) cos

dx,

l l

1 l

f (x ) sin

dx,

n 12,, ... .

Если f(x) – кусочно-гладкая функция на отрезке [–l,l], то ее ряд Фурье сходится в каждой точке отрезка [–l,l]. При этом сумма S(x), x [–l,l], ряда Фурье равна

		f (x),					если x	точка непрерывности f (x);
S (x)		1	( f (x0	0)	f (x0	0)),	если x	x0 точка разрыва f (x);
		2

		1	( f ( l	0)	f (l	0)),	если x	l или x l.
		2

	Пример 1. Разложить в ряд Фурье по синусам функцию
f ( x)			x,	0 x	1,
		2 x, 1 x 2 .

	Решение. Продолжим f(x) на интервале (–2,0) нечетным об-
разом. Тогда a0				0, an 0 ; при l=2 получаем:

2 l

f ( x) sin

x sin

x) sin

1)k

если

2k 1,

sin

(2k

1)2

если

2k .

Следовательно, разложение в ряд Фурье имеет вид:

f (x )	8	(	1) k	sin	(2k	1) x	, 0 x 2 .
	2 k 0	(2k	1) 2			2

2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕНЫХ

2.1.Определенный интеграл по фигуре. Основные понятия и свойства

Пусть функция f(x,y,z) задана в точках тела W, на поверхности тела Т или кривой Г в декартовой системе координат Oxyz. Разобьем указанные фигуры на n частей Wi, Ti, Гi соответственно и на каждой из частей выберем по одной точке (xi, yi, zi).

Меры полученных частей разбиения обозначим через							Vi (обьем
части),		Si (площадь части) и Li (длина части) соответственно.
Через	i	обозначим наибольшее из расстояний между любыми
	i

двумя точками,			взятыми на i-ой части разбиения, i			1, n . Число
max		i , 1 i	n , показывает, насколько мелко разбиты фигу-
ры, и называется диаметром разбиения.
Составим теперь интегральные суммы:
			W	n
			W		f (x i , yi , zi ) V i ;
			n		f (x i , yi , zi ) V i ;
				i	1
			T	n
			T		f (x i , yi , zi ) S i ;
			n		f (x i , yi , zi ) S i ;
				i	1
			Г	n
			Г		f (x i , yi , zi ) L i .
			n		f (x i , yi , zi ) L i .
				i	1

Если существуют конечные пределы этих интегральных сумм при 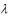0, причем эти пределы не зависят от способа разбиения фигур и от выбора точек на частях разбиения, то они на-

зываются определенными интегралами функции f(x,y,z) по на-

званным фигурам:

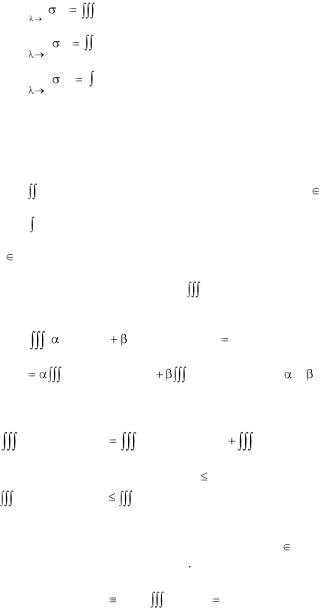
	lim	w
		n
	0
		w

f (x, y, z)dx dydz – тройной интеграл;

lim	s	f (x, y, z)ds	– поверхностный интеграл I рода;
	n
0
		s

lim	Г	f (x, y, z)dl	– криволинейный интеграл I рода.
	n
0
		Г

Физический смысл интеграла по фигуре.

Если f(x,y,z) – плотность распределения вещества по фигуре, то интеграл по этой фигуре выражает ее массу в соответствующих единицах измерения.

Замечание. Аналогично названным вводятся интегралы:

f (x, y, z)dx dy	– двойной интеграл по области D		Oxy;
D
f (x, y)dl – криволинейный интеграл I рода по кривой
Г
Г Oxy.
Свойства интегралов по фигуре
(на примере тройного интеграла		f (x, y, z)dx dydz ).
		v
1. Свойство линейности.
( f (x, y, z)	g(x, y, z))dxdydz
w
f (x, y, z)dx dydz		g(x, y, z)dx dydz; и	– числа.
w	w

2. Если область W есть объединение двух областей W1 и W2, не имеющих общих внутренних точек, то

f (x, y, z)dxdydz	f (x, y, z)dxdydz	f (x, y, z)dxdydz.
w	w1	w2
3. Если в области W: f (x, y, z) g(x, y, z) , то
f (x, y, z)dx dydz	g(x, y, z)dx dydz.
w	w

4. Теорема о среднем. Если f(x,y,z) непрерывна в замкнутой связной области W, то найдется точка (x*,y*,z*) W такая, что

f (x, y, z)dx dydz f (x *, y*, z*) V , где V – объем тела W. w

5. Если f(x,y,z) 1, то 1dxdydz V .

Предполагается, что все указанные интегралы существуют.

2.2.Вычисление двойных и тройных интегралов

вдекартовых координатах

а) Двойной интеграл. Пусть область D плоскости Oxyz ограничена линиями y= (x), y= (x), x=a, x=b, где a<b, (x)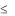 (x) и функции , непрерывны на отрезке [a; b] (рис.2.1). Двойной интеграл от непрерывной функции f(x,y) вычисляется путем сведения к двукратному интегралу по формуле

	b		(x )
	f (x, y)dx dy	dx	f (x, y)dy.	(2.1)
D	a		(x )

y= (x)

y D axxy aDx

y= (x)

Рис. 2.1

(x )

В выражении (2.1) сначала вычисляется

f (x, y)dy при

(x )

постоянном x. Полученный результат интегрируется по x. Аналогично, если область D ограничена линиями x= (y),

x= (y), y=c, y=d, где c<d, (y)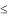(y) и функции и непрерывны на отрезке [c; d] (рис.2.2), то

	d	( y)
	f (x, y)dx dy	dy f (x, y)dx.	(2.2)
D	c	( y)

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.08.20198.02 Mб77Краткий конспект по Промышленным зданием.doc
#
20.11.201866.05 Кб14Кризис. псих.doc
#
31.05.20152.44 Mб167Круглов В.А.весь.doc
#
26.03.201636.97 Mб593КРУПНОЭЛЕМЕНТНОЕ И МОНОЛИТНОЕ ДОМОСТРОЕНИЕ.docx
#
26.09.20192.43 Mб12КРЭА шпорки1-40.docx
#
31.05.20152.37 Mб8КР№3 НАША ПО МАТЕМАТИКЕ.pdf
#
22.11.20191.79 Mб2КС Word.doc
#
10.07.2019261.12 Кб20КТП 12 кл.2010.doc
#
18.11.2018156.16 Кб8КУЛЬТУРА БЕЛАРУСІ XIX - пачатку XX стст..doc
#
18.11.2018144.38 Кб6КУЛЬТУРА БЕЛАРУСІ XIX - пачатку XX стст..doc
#
23.11.20192.12 Mб15Культура Беларусі.rtf