58 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
preemptable, and periodic tasks with relative deadlines the same as the corresponding periods on a uniprocessor such that the periods satisfy ps < p1 < p2 < · · · < pn < 2 ps and pn > ps + cs is RM-schedulable if the total utilization of this task set (including the DS) is at most
U (n) = (n − 1) |
|
Us |
+ |
1 |
|
1 |
|
− 1 . |
|
− |
|
||||||
|
|
+ |
2 |
|
|
|
||
|
|
Us |
|
|
n |
1 |
|
|
3.2.2 Scheduling Nonpreemptable Tasks
So far we have assumed that tasks can be preempted at any integer time instants. In practice, tasks may contain critical sections that cannot be interrupted. These critical sections are needed to access and modify shared variables or to use shared resources such as disks. Now we consider the scheduling of nonpreemptable tasks and tasks with nonpreemptable subtasks. An important goal is to reduce task waiting time and context-switching time [Lee and Cheng, 1994]. Using fixed-priority schedulers for non-real-time tasks may potentially lead to the priority inversion problem [Sha, Rajkumar, and Lehoczky, 1990], which occurs when a low-prioirty task with a critical section blocks a higher-priority task for an unbounded or long period of time.
The EDF and LL algorithms are no longer optimal if the tasks are not preemptable. For instance, without preemption, we cannot transform a feasible non-EDF schedule into an EDF schedule by interchanging computation blocks of different tasks as described in the proof of EDF optimality. This means that the EDF algorithm may fail to meet a deadline of a task set even if another scheduler can produce a feasible schedule for this task set. In fact, no priority-based scheduling algorithm is optimal for nonpreemptable tasks with arbitrary start times, computations times, and deadlines, even on a uniprocessor [Mok, 1984].
Scheduling Nonpreemptable Sporadic Tasks As above, we apply the scheduling strategies for periodic tasks introduced earlier by first transforming the sporadic tasks into equivalent periodic tasks [Mok, 1984], yielding the following schedulability test.
Schedulability Test 8: Suppose we have a set M of tasks that is the union of a set Mp of periodic tasks and a set Ms of sporadic tasks. Let the nominal (or initial) laxity li of task Ti be di − ci . Each sporadic task Ti = (ci , di , pi ) is replaced by an equivalent periodic task Ti = (ci , di , pi ) as follows:
ci = ci
pi = min( pi , li + 1) di = ci .
If we can find a feasible schedule for the resulting set M of periodic tasks (which includes the transformed sporadic tasks), we can schedule the original set M of tasks
UNIPROCESSOR SCHEDULING |
59 |
without knowing in advance the start (release or request) times of the sporadic tasks in Ms .
A sporadic task (c, d, p) can be transformed into and scheduled as a periodic task (c , d , p ) if the following conditions hold: (1) d ≥ d ≥ c, (2) c = c, and
(3) p ≤ d − d + 1. A proof can be found in [Mok, 1984].
3.2.3 Nonpreemptable Tasks with Precedence Constraints
So far we have described scheduling strategies for independent and preemptable tasks. Now we introduce precedence and mutual exclusion (nonpreemption) constraints to the scheduling problem for single-instance tasks (tasks that are neither periodic nor sporadic) on a uniprocessor.
A task precedence graph (also called a task graph or precedence graph) shows the required order of execution of a set of tasks. A node represents a task (or subtask) and directed edges indicate the precedence relationships between tasks. The notation Ti → Tj means that Ti must complete execution before Tj can start to execute. For task Ti , incoming edges from predecessor tasks indicate all these predecessor tasks have to complete execution before Ti can start execution. Outgoing edges to successor tasks indicate that Ti must finish execution before the successor tasks can start execution. A topological ordering of the tasks in a precedence graph shows one allowable execution order of these tasks.
Suppose we have a set of n one-instance tasks with deadlines, all ready at time 0 and with precedence constraints described by a precedence graph. We can schedule this task set on a uniprocessor with the algorithm shown in Figure 3.12.
This algorithm executes a ready task whose predecessors have finished execution as soon as the processor is available.
Example. Consider the following tasks with precedence constraints:
T1 → T2
T1 → T3
T2 → T4
T2 → T6
Algorithm:
1.Sort the tasks in the precedence graph in topological order (so that the task(s) with no in-edges are listed first). If two or more tasks can be listed next, select the one with the earliest deadline; ties are broken arbitrarily.
2.Execute tasks one at a time following this topological order.
Figure 3.12 Scheduling algorithm A for tasks with precedence constraints.
60 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
T6
T2
T4
T1
T3 
T5
Figure 3.13 Precedence graph.
T3 → T4
T3 → T5
T4 → T6.
The precedence graph is shown in Figure 3.13. The tasks have the following computation times and deadlines:
T1: c1 = 2, d1 = 5,
T2: c2 = 3, d2 = 7,
T3: c3 = 2, d3 = 10,
T4: c4 = 8, d4 = 18,
T5: c5 = 6, d5 = 25, and
T6: c6 = 4, d6 = 28.
A variation of this algorithm, shown in Figure 3.14, is to lay out the schedule by considering the task with the latest deadline first and then shifting the entire schedule toward time 0.
Algorithm:
1.Sort the tasks according to their deadlines in non-decreasing order and label the tasks such that d1 ≤ d2 ≤ · · · ≤ dn .
2.Schedule task Tn in the time interval [dn − cn , dn ].
3.While there is a task to be scheduled do
Suppose S is the set of all unscheduled tasks whose successors have been scheduled. Schedule as late as possible the task with the latest deadline in S.
4.Shift the tasks toward time 0 while maintaining the execution order indicated in step 3.
Figure 3.14 Scheduling algorithm B for tasks with precedence constraints.
UNIPROCESSOR SCHEDULING |
61 |
|
|
|
|
|
T1 T2 |
|
|
|
T3 |
|
|
|
|
|
T4 |
|
|
|
|
|
|
|
|
T5 |
|
|
|
|
|
|
T6 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
time |
||||||||
0 |
5 |
|
|
10 |
15 |
20 |
|
|
25 |
|
|
30 |
|||||||||||||||||||||||||||||||||||||||||||||
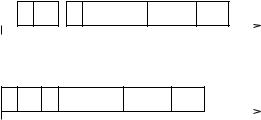
Figure 3.15 Schedule for tasks with precedence constraints.
|
|
T1 T2 T3 |
|
|
|
|
|
|
T4 |
|
|
|
|
|
|
|
|
|
|
T5 |
|
|
|
|
|
|
T6 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
time |
|||||||||
0 |
5 |
|
|
10 |
|
|
15 |
|
|
|
|
|
|
20 |
25 |
30 |
||||||||||||||||||||||||||||||||||||||||||
Figure 3.16 Schedule for tasks with precedence constraints after shifting tasks.
Step 1 of the algorithm A sorts the tasks in topological order: T1, T2, T3, T4, T5, T6. Note that tasks T2 and T3 are concurrent; so are pair T4 and T5 and pair T5 and T6. Step 2 of the algorithm produces the schedule shown in Figure 3.16.
Using scheduling algorithm B, we obtain the feasible schedule before shifting tasks, shown in Figure 3.15. Figure 3.16 shows the feasible schedule produced by the scheduler after shifting tasks toward time 0.
3.2.4Communicating Periodic Tasks: Deterministic Rendezvous Model
Allowing tasks to communicate with each other complicates the scheduling problem. In fact, interprocess communication leads to precedence constraints not only between tasks but also between blocks within these tasks. For example, the Ada programming language provides the primitive rendezvous to allow one task to communicate with another at a specific point during the task execution. Ada is used in the implementation of a variety of embedded and real-time systems, including airplane avionics. If a task A wants to communicate with process B, task A executes rendezvous(B). Task A then waits until task B executes a corresponding rendezvous(A).
As a result, these pair of rendezvous impose a precedence constraint between the computations of tasks A and B by requiring that all the computations prior to the rendezvous primitive in each task be completed before the computations following the rendezvous primitive in the other task can start. To simplify our scheduling strategy, we assume here that the execution time of a rendezvous primitive is zero or that its execution time is included in the preceding computation block.
A one-instance task can rendezvous with another one-instance task. However, it is semantically incorrect to allow a periodic task and a sporadic task to rendezvous with each other since the sporadic task may not run at all, causing the periodic task to wait forever for the matching rendezvous. Two periodic tasks may rendezvous with each other, but there are constraints on the lengths of their periods to ensure correctness.
Two tasks are compatible if their periods are exact multiples of each other. To allow two (periodic) tasks to communicate in any form, they must be compatible. One attempt to schedule compatible and communicating tasks is to use the EDF scheduler to execute the ready task with the nearest deadline that is not blocked due to a rendezvous.
62 REAL-TIME SCHEDULING AND SCHEDULABILITY ANALYSIS
The solution [Mok, 1984] to this scheduling problem starts by building a database for the runtime scheduler so that the EDF algorithm can be used with dynamically assigned task deadlines. Let L be the longest period. Since the communicating tasks are compatible, L is the same as the LCM of these tasks’ periods. We denote a chain of scheduling blocks generated in chronological order for task Ti in interval [0, L] by
Ti (1), Ti (2), . . . , Ti (mi ).
If there is a rendezvous constraint with Ti targeting Tj between
Ti (k) and Ti (k + 1),
Tj (l) and Tj (l + 1),
then the following precedence relations are specified:
Ti (k) → Tj (l + 1),
Tj (l) → Ti (k + 1).
Within each task, the precedence constraints are:
Ti (1) → Ti (2) → . . . → Ti (mi ).
After generating the precedence graph corresponding to these constraints, we use the algorithm shown in Figure 3.17 to revise the deadlines.
Example. Consider the following three periodic tasks:
T1: c1 = 1, d1 = p1 = 12.
T2: c2,1 = 1, c2,2 = 2, d2 = 5, p2 = 6.
T3: c3,1 = 2, c3,2 = 3, d3 = 12, p3 = 12.
T2 must rendezvous with T3 after the first scheduling block.
T3 must rendezvous with T2 after the first and second scheduling blocks.
Algorithm:
1.Sort the scheduling blocks in [0, L] in reverse topological order, so the block with the latest deadline appears first.
2.Initialize the deadline of the kth instance of Ti, j to (k − 1)pi + di .
3.Let S and S be scheduling blocks; the computation time and deadline of S are respec-
tively denoted by cS and dS . Considering the scheduling blocks in reverse topological order, revise the corresponding deadlines by dS = min(dS , {dS − cS : S → S }).
4.Use the EDF scheduler to schedule the blocks according to the revised deadlines.
Figure 3.17 Scheduling algorithm for tasks with rendezvous constraints.