1. Метод комплексных амплитуд

1.1. Гармонический сигнал

Гармонический сигнал записывают в виде

, (1.1)

где - амплитуда сигнала (индексот слова «максимум»),- круговая частота, а- начальная фаза. Временная диаграмма гармонического сигналапоказана на рис. 1.1.

Рис. 1.1

Амплитуда гармонического сигнала – это его максимальное значение, она измеряется в единицах сигнала (вольтах для напряжения и амперах для тока).

Период сигнала (рис. 1.1) определяетциклическую частоту его повторения,

, (1.2)

измеряемую в герцах (Гц). Ее физический смысл – число периодов колебаний в секунду.

Аргумент косинуса в (1.1) вида

4

(1.3)

называют полной фазой колебания, она пропорциональна текущему времени и измеряется в радианах или градусах.

Круговая частота равна

(1.4)

и представляет собой число радиан, на которое изменяется полная фаза колебания в единицу времени (1 с).

При полная фаза равна, поэтому параметрназываютначальной фазой гармонического сигнала. Она измеряется в радианах или градусах. Так как период функции равенили 360⁰, то начальная фаза оказывается многозначной величиной. Например, значения начальной фазы 30⁰ и (30⁰+360⁰)=390⁰, а также (30⁰-360⁰)=-330⁰ оказываются эквивалентными. Для устранения неоднозначности договариваются, что значения начальной фазы должны находиться, например, в интервале от 0 до , или отдо(аналогичные границы могут быть заданы в градусах).

Начальная фаза связана со смещением гармонического сигнала во времени на величину относительно функции, как показано на рис. 1.1. Функциясмещена влево относительно, а- вправо.Положительные значения отсчитываются в сторонуувеличения , а отрицательные – наоборот.

Из (1.1) можно записать

, (1.5)

5

где смещение во времени равно

. (1.6)

Тогда для начальной фазы получим

. (1.7)

Как видно, начальная фаза определяется временным сдвигом гармонического сигнала относительно функции. Присигналсмещается вправо по оси времени, при этом его начальная фаза, а если, то временная диаграмма смещается влево по оси времени, а. Величина начальной фазы зависит от начала отсчета времени (положения точки). При смещении начала отсчета времени изменяется и начальная фаза.

Применительно к двум гармоническим сигналам ис разными начальными фазамиивводится в рассмотрениесдвиг фаз между первым и вторым сигналами,

. (1.8)

На рис. 1.2 показаны два гармонических сигнала с начальными фазами и, причеми. В этом случае говорят, что первый сигналопережает по фазе второй или второй сигнал отстает по фазе от первого.

Сдвиг фаз связан со смещениемсигналов во времени

, (1.9)

6

п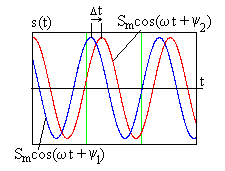оложительные значения временного сдвига отсчитываются в направлении оси времени. Гармоническое колебание может быть задано в нетипичной форме, которую необходимо преобразовать к виду (1.1), иначе начальная фаза

Рис. 1.2 оказывается неопреде-

ленной. Примеры преобразования показаны в табл. 1.1.

Таблица 1.1.

Исходный сигнал	Преобразованный сигнал	Начальная фаза

1.2. Комплексная амплитуда гармонического сигнала

Для гармонического сигнала (тока или напряжения) комплексная амплитуда равна

, .(1.10)

Комплексная амплитуда является комплексным числом (-мнимая единица) и определяется только амплитудой и начальной фазой сигнала и не зависит от его час-

7

тоты. Комплексная амплитуда обозначается тем же символом, что и амплитуда сигнала, но с точкой сверху.

Например, если мгновенное значение гармонического напряжения равно В, то его комплексная амплитуда равнаВ илиВ.

Если запись сигнала отличается от формы (5.1) то необходимо провести соответствующие тригонометрические преобразования, представленные в табл. 1.2.

Таблица 1.2.

Если гармоническое напряжение имеет вид мВ, то после преобразования получиммВ, а комплексная амплитуда будет равнамВ.

1.3. Операции с комплексными числами

Комплексные числа могут быть записаны в двух формах: алгебраической и показательной. В алгебраической форме комплексное число (точка сверху используется для обозначения комплексной амплитуды сигнала, а если речь идет о комплексном сопротивлении или проводимости, то используется подчеркивание символа) записывается в виде

8

, (1.12)

где -действительная, а -мнимая части комплексного числа, -мнимая единица.

В показательной форме комплексное число представляется выражением

, (1.13)

величину называютмодулем, а -аргументом комплексного числа. От алгебраической формы можно перейти к показательной, модуль комплексного числа равен

, (1.14)

а аргумент

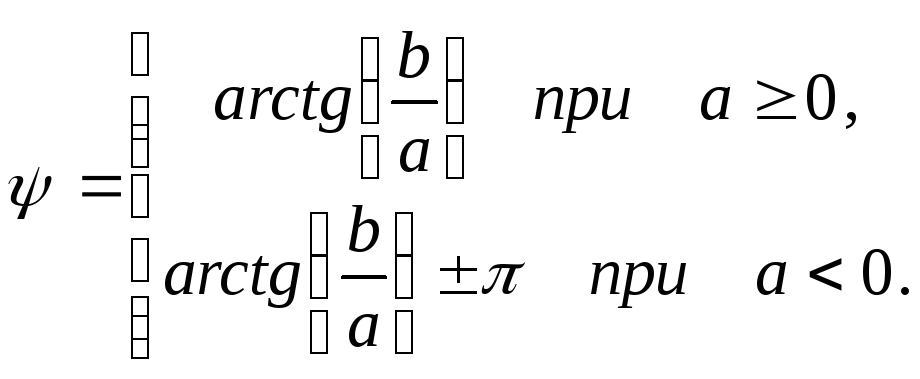(1.15)

Аргумент комплексного числа, как и начальная фаза гармонического сигнала, величина многозначная, к ней можно добавить (или вычесть) любое число раз. Для обеспечения однозначности аргумента комплексного числа его значения выбирают в диапазоне, например, отдоили от 0 до.

Показательную форму комплексного числа можно заменить алгебраической с помощью соотношений

(1.16)

Они вытекают из известной в математике формулы Эйлера,

9

(1.17)

Например, если комплексное число в алгебраической форме равно , то в показательной форме его можно записать в виде

.

Если комплексное число равно , то в показательной форме получим

.

Для комплексного числа в показательной форме в виде его алгебраическая форма имеет вид

.

С комплексными числами проводятся все четыре арифметические действия.

При сложении и вычитании комплексных чисел ив алгебраической форме получим

. (1.18)

Если числа заданы в показательной форме, то перед сложением или вычитанием их необходимо преобразовать в алгебраическую форму.

Операции умножения и деления удобнее выполнять в показательной форме, когда и, при этом при умножении комплексных чисел их модули перемножаются, а аргументы складываются

10

, (1.19)

а при делении делятся модули и вычитаются аргументы числителя и знаменателя

. (1.20)

Умножение можно провести и с алгебраической формой сомножителей по известным правилам с учетом того, что :

. (1.21)

При делении комплексных чисел в алгебраической форме используется операция устранения комплексности в знаменателе путем умножения числителя и знаменателя дроби на число, комплексно сопряженное знаменателю. Для заданного числа комплексно сопряженное числоравно, то есть отличается отпротивоположным знаком примнимой части. Произведение двух комплексно сопряженных чисел всегда равно квадрату их модуля,

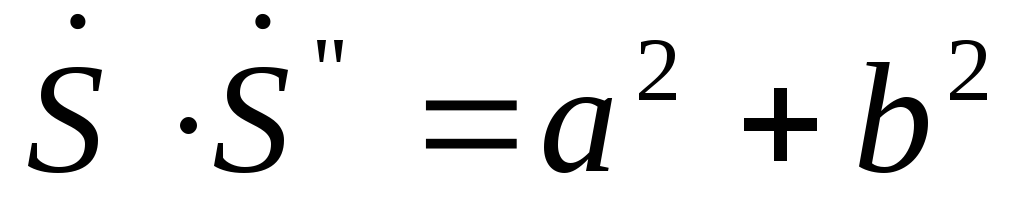. (1.22)

Тогда при делении в алгебраической форме получим

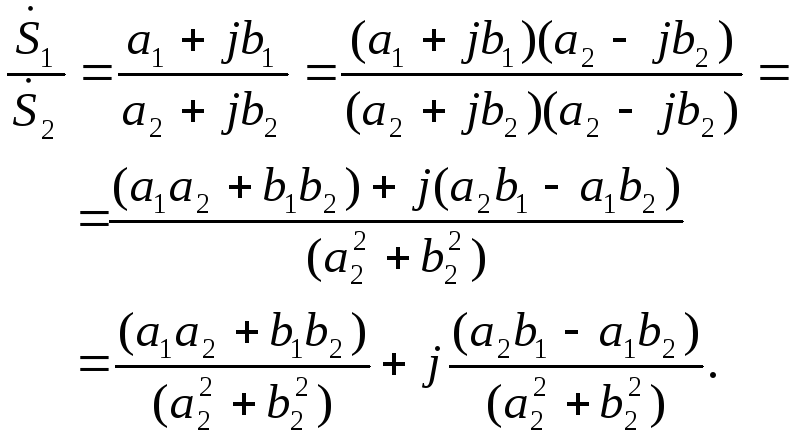(1.23)

11

Рассмотрим пример и, тогда

,

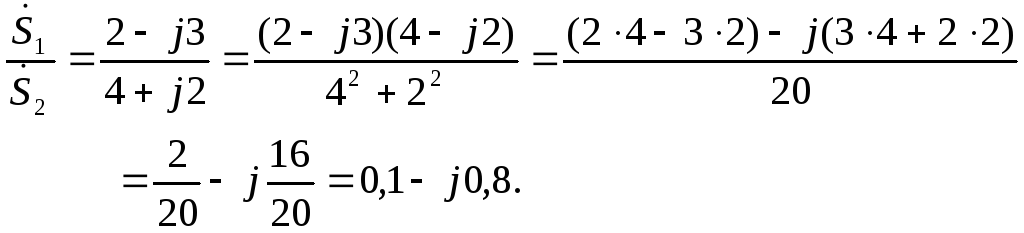
Эти операции можно провести и в показательной форме

,

,

,

.

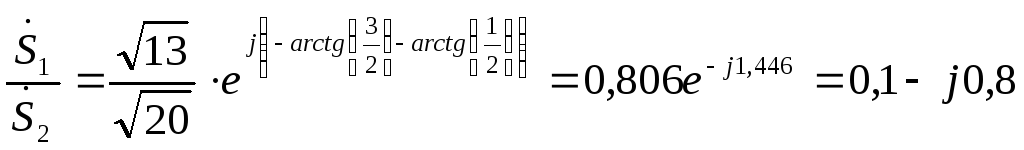Как видно, полученные результаты совпадают.

Полезно запомнить следующие равенства (табл. 1.3.), вытекающие из формулы Эйлера,

(1.24)

12

Таблица 1.3.

Вычисления с комплексными числами удобно проводить на персональной ЭВМ с помощью пакета программ MathCAD.

1.4. Законы Ома и Кирхгофа для комплексных

амплитуд токов и напряжений

Законы Ома и Кирхгофа применимы в своих классических формулировках для комплексных амплитуд токов и напряжений.

Закон Ома: комплексная амплитуда напряжения на участке цепи прямо пропорционально комплексной амплитуде протекающего через него тока. Для двухполюсного участка цепи его можно записать в виде

или , (1.25)

где -полное комплексное сопротивление, а -полная комплексная проводимость участка цепи.

Первый закон Кирхгофа: алгебраическая сумма комплексных амплитуд сходящихся в узле токов равна нулю,

. (1.26)

Второй закон Кирхгофа: алгебраическая сумма комплексных амплитуд падений напряжения на элементах замкнутого контура равна алгебраической сумме комплексных амплитуд ЭДС идеальных источников напряжения, включенных в этот контур,

13

. (1.27)

Знаки в алгебраических суммах определяются выбранными положительными направлениями токов и напряжений и направлением обхода контура.

1.5. Комплексные сопротивления и проводимости

элементов цепи

Значения комплексных сопротивлений и проводимостейэлементов цепиR, L и C приведены в табл. 1.4 (запомните эти формулы).

Таблица 1.4

Элемент	R	L	C
Комплексное сопротивление
Комплексная проводимость

Комплексные сопротивление и проводимость сопротивления всегдадействительны (мнимая часть равна нулю), а индуктивности и емкости – мнимые (действительная часть равна нулю).

Для комплексного сопротивления из закона Ома получим

, (1.28)

где -сдвиг фаз между напряжением и током в

14

элементе. Для сопротивления напряжение и ток совпадают по фазе, то естьи из (1.28) величинадействительна.

В индуктивности напряжение опережает по фазе ток на 90⁰ (на радиан), следовательно, тогдаи величина комплексного сопротивления индуктивностиоказывается снулевой действительной и положительной мнимой частями. В емкости ,и ее комплексное сопротивление имеетнулевую действительную и отрицательную мнимую части.

1.6. Комплексные сопротивление и проводимость

участка цепи

Полные комплексные сопротивления (и проводимости) двухполюсного участка цепи с произвольным соединением элементов определяются по следующим правилам:

- комплексное сопротивление последовательного соединения двухполюсников равно сумме их комплексных сопротивлений;

- комплексная проводимость параллельного соединения двухполюсников равна сумме их комплексных проводимостей.

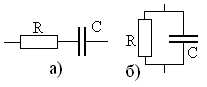Например, сопротивление последовательной цепи, показанной на рис. 1.3а прикОм ипФ и частотекГц равно

кОм,

Рис. 1.3 а проводимость параллельной це-

пи на рис 5.1б -

Сим.

Зная комплексное сопротивление цепи, можно определить ее комплексную проводимость и наоборот,

15

(1.29)

Для последовательной цепи на рис. 1.3а ее проводимость равна

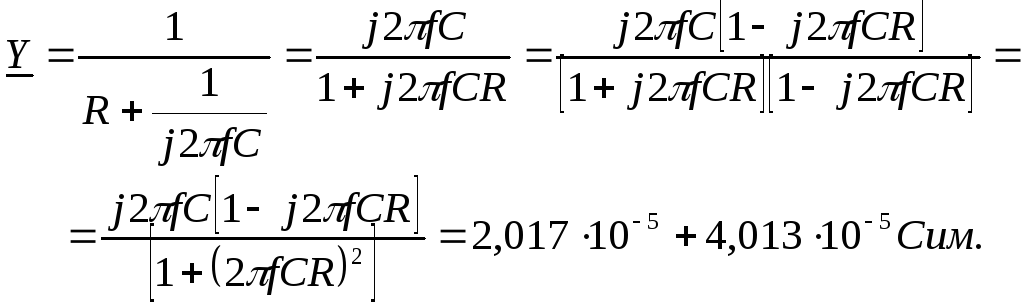
Расчет проведен методом устранения комплексности знаменателя путем умножения числителя и знаменателя дроби на множитель, комплексно-сопряженный знаменателю. Можно провести вычисление проводимости путем преобразования комплексного сопротивления из алгебраической формы в показательную,

.

Тогда для проводимости получим

Сопротивлениепараллельного соединения двух элементов с сопротивлениями иопределяется выражением

.

Комплексное сопротивление цепи со смешанным со-

16

единением элементов определяется следующим образом:

- в цепи выделяется фрагмент с простым (последовательным или параллельным) соединением элементов и определяется его сопротивление или проводимость;

- фрагмент заменяется эквивалентным элементом, в полученной цепи вновь выделяется простой фрагмент и повторяется предыдущее действие;

- эти действия повторяются до тех пор, пока цепь не трансформируется в один элемент с соответствующим сопротивлением или проводимостью.

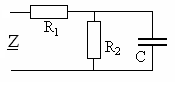Рассмотрим цепь, схема которой показана на рис. 1.4 прикОм,нФ,рад/с и определим ее комплексное сопротивление . В цепи выделяется простой параллельный фрагмент из элементовиопределяется его сопротивление , равное

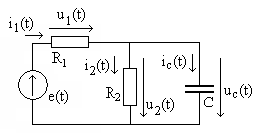Рис. 1.4 .

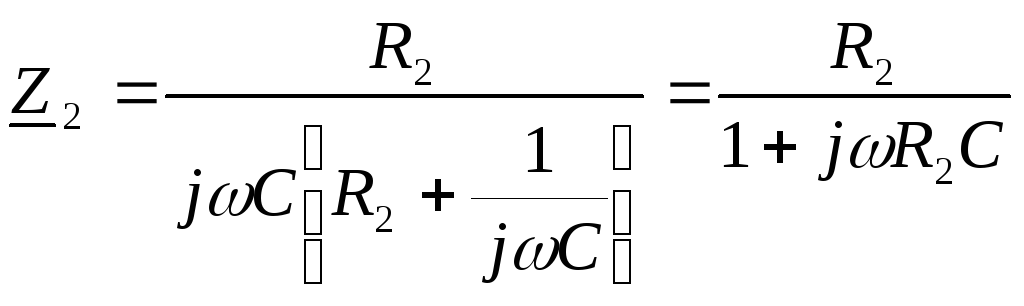Тогда параллельный фрагмент заменяется эквивалентным элементом с сопротивлениеми схема цепи принимает вид, показанный на рис. 1.5.

Для полученной последовательной цепи ее сопротивлениеравно

.

Подставляя исходные данные, получим

Рис. 1.5

Ом.

17