Статистика

Тогда ранговый коэффициент корреляции Спирмена вычисляется по формуле:

где tγ , f − пороговое значение распределения Стьюдента с параметрами

γ =1−α2 , f = n − 2 . В противном случае, гипотезаотклоняется.

Если необходимо определить степень тесноты статистической

Здесь

m − количество выбранных для анализа ранжировок; n − длина ранжировок;

k j , j =1, m − номера отобранных для анализа ранжировок.

0 ≤W (m)≤1.

33

Формула (4.4.4) также пригодна только для случая, если ни одна из исследуемых ранжировок не содержит повторяющихся рангов. Иначе, используя поправки (4.3.2), коэффициент конкордации рассчитывается по формуле:

Для проверки гипотезы об отсутствии статистически значимой корреляционной связи между выбранными ранжировками проверяется гипотеза

H0 : W (m)= 0 .

Гипотеза H0 принимается при уровне значимости α = 0.05 , если m(n −1)Wˆ (m)< χα2,n−1 .

Впротивном случае, гипотеза отклоняется.

Задача.

Втаблице приведены данные успеваемости учеников одного класса по математике, физике, литературе и иностранному языку.

34

Определить, есть ли связь между успеваемостью учащихся по каждой паре предметов.

Решение. Применение пакета Statistica для расчетов коэффициентов Спирмена дает следующие результаты:

35

«Математика – Физика» и «Литература – Иностранный язык», в то время, как для других пар предметов такой связи нет. Так, например, если учащийся имеет хорошие результаты по математике, у него, вероятно, будут хорошие результаты по физике, при этом это ничего не говорит об его успеваемости по другим предметам. И наоборот.

4.4 Корреляционный анализ категоризованных данных. Таблицы сопряженности.

Пусть рассматриваются n объектов на наличие в них двух признаков A и B . Пусть при этом признак A может иметь m различных значений, а B − k различных значений. Обозначим через nij количество элементов выборки, обладающих i -тым значением признака A и j -тым значением признака B . Предполагается, что один и тот же объект не может обладать одновременно несколькими уровнями одного признака.

Необходимо установить, влияет ли наличие у объекта признака A , на проявление в нем признака B , или обуславливает ли изменение уровней признака A изменения признака B .

36

Категоризованные данные – это набор перекрестных частот nij ,

i =1, m , j =1, k , ∑nij = n двух признаков A и B , значения которых

i, j

зафиксированы на конечном числе уровней. Данные (частоты) представляются в таблице сопряженности следующего вида:

Статистический анализ перекрестных частот позволяет ответить на вопрос о существовании зависимости между признаками непараметрически, т.е. при неизвестных распределениях рассматриваемых величин.

Степень тесноты статистической зависимости двух признаков можно определить с помощью коэффициента X 2 квадратичной сопряженности признаков A и B

37

Величина X 2 равна нулю при строгой статистической независимости признаков A и B . С ростом степени зависимости признаков величина X 2 может расти до +∞ . В предположении статистической независимости переменных A и B величина X 2

имеет χ2 -распределение с (m −1)(k −1) степенями свободы. Если выполнено неравенство

X 2 < χα2,(m−1)(k−1) ,

при уровне значимости α гипотеза H0 об отсутствии значимой статистической связи между A и B принимается.

Замечание. Аналогичным образом проверяется гипотеза о независимости двух случайных выборок. В этом случае в качестве уровней признаков берутся варианты рассматриваемых случайных величин.

Самый простой случай, когда признаки имеют всего два возможных уровня: наличие это признака у объекта, либо его отсутствие. Тогда таблица сопряженности имеет вид:

Тогда условие независимости признаков A и B по теореме умножения вероятностей может записано в виде

P(A)= P(A | B)= P(A | B ),

38

и B отрицательно связаны.

По статистическим данным получить равенство крайне сложно, поэтому речь идет о степени отклонения от него. Величиной характеризующей это отклонение является

На базе нее строится коэффициент сопряженности в виде:

39

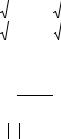
Тогда гипотеза об отсутствии статистически значимой корреляционной связи между исследуемыми признаками принимается, если

В противном случае гипотеза отклоняется и выносится решение о статистической связи.

Также может быть использован коэффициент

который, очевидно, связан с Q следующим соотношением

Q= 1+2ΥΥ2 .

Υ≤1.

Υ= 0 и Q = 0 при статистической независимости признаков A и B .

40