2.8 Задача д3. Теорема изменения кинетической энергии

механической системы

Механическая система, состоящая из твердых тел 1, 2, 3, 4, соединенных гибкими, невесомыми, нерастяжимыми нитями, под действием сил тяжести приходит в движение из состояния покоя. Учитывая трение скольжения тела 3, катящегося без скольжения, определить скорость груза 1 в тот момент, когда, опускаясь, он пройдет путь s.

Другие сопротивления не учитывать. Коэффициент трения скольжения f = 0,1; трения качения δ = 2 * 10^-3 м. Углы наклона плоскостей α и β принять равными 30º, 45º или 60º. Тела 2 и 3 считать однородными дисками, если они одноступенчатые. Если на рисунке Д3 они показаны двухступенчатыми, то их моменты инерции определить через указанные в таблице Д3 радиусы инерции ρ₂ и ρ₃.

Таблица Д3 Данные к задаче Д3

Номер условия	m1, кг	m2, кг	m3, кг	m4, кг	R2, м	r2, м	ρ2, м	R3, м	r3, м	ρ3, м	S, м
1	2	3	4	5	6	7	8	9	10	11	12
0	25	10	7	3	0,6	0,4	0,5	0,4	0,3	0,4	2
1	30	8	9	5	0,5	0,3	0,4	0,4	0,2	0,3	2
2	40	12	10	8	0,5	0,3	0,4	0,4	0,2	0,3	3
3	35	14	8	7	0,4	0,3	0,3	0,3	0,2	0,2	2
4	30	10	10	5	0,4	0,3	0,4	0,3	0,2	0,3	3
5	25	8	7	6	0,4	0,3	0,3	0,3	0,2	0,3	3
6	50	15	12	10	0,5	0,3	0,4	0,4	0,2	0,3	3
7	45	15	12	8	0,6	0,3	0,5	0,5	0,3	0,4	2
8	35	15	10	5	0,4	0,2	0,3	0,3	0,2	0,3	3
9	50	20	10	8	0,4	0,3	0,4	0,3	0,2	0,2	2

Пример Д3. Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на рисунках. Учитывая трение скольжения тела 1 и сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s. Тело 2 и 3 считать сплошными однородными цилиндрами.

Дано: – масса груза 1,,,м,,, коэффициент трения скольжения, коэффициент трения качениясм,м. На рис. Д3 показана механическая схема в начальном положении.

Найти: – скорость груза 1 в конечном положении.

Решение. Применим теорему об изменении кинетической энергии системы:

(1)

где Т₀ и Т – кинетическая энергия системы в начальном и конечном положениях; - сумма работ внешних сил, приложенных к системе, на перемещение системы из начального положения в конечное; - сумма работ внутренних сил системы на том же перемещении.

Для рассматриваемых систем, состоящих из абсолютно твёрдых тел, соединенных нерастяжимыми нитями и стержнями,

Так как в начальном положении система находится в покое, то Т₀ = 0.

Следовательно, уравнение (1) принимает вид

(2)

Напишем кинематические соотношения между скоростями и перемещениями точек системы, т. е. уравнения связей, при этом перемещения и скорости тел выразим соответственно через скорости и перемещения груза 1.

Скорость центра масс катка 3 равна скорости груза 1:

. (3)

Угловая скорость катка 3, мгновенный центр скоростей которого находится в точке касания катка с плоскостью

. (4)

Угловая скорость блока 2 . (5)

Вычислим кинетическую энергию системы в конечном положении как алгебраическую сумму кинетических энергий тел 1, 2, 3:

. (6)

Кинетическая энергия груза 1, движущегося поступательно,

. (7)

Кинетическая энергия блока 2, вращающегося вокруг оси Ax:

. (8)

Момент инерции блока 2 относительно оси Ax:

. (9)

Подставляя выражения (5), (9) в формулу (8), получаем

.

Кинетическая энергия катка 3, совершающего плоское движение:

, (10)

где - момент инерции катка 3 относительно его продольной центральной оси :. (11)

Подставляя (3), (4), (11) в формулу (10), получаем

. (12)

Кинетическая энергия всей системы:

. (13)

Найдём сумму работ всех внешних сил, приложенных к системе на заданном ее перемещении. Покажем внешние силы, приложенные к системе (рис. Д3.1): для тела 1:

Работа сил тяжести G₁ :

(14)

Работа силы трения скольжения F_тр:

.

Так как ,

то . (15)

для катка 3:

Работа силы тяжести G₃ будет отрицательной, т.к. начальное положение катка выше, чем конечное

. (16)

Работа силы сцепления катка , т.к. сила приложена в мгновенном центре скоростей катка.

Работа пары сил сопротивления качению катка 3:

где - момент пары сил сопротивления качению катка 3; - угол поворота катка 3.

Так как каток катится без скольжения, то угол его поворота

где S_C3 – перемещение центра тяжести С₃ катка 3.

В нашем случае перемещение центра масс катка 3 будет равно перемещению центра масс груза 1, т.е. S_C3 = S = 2,4 м.

Тогда работа пары сил сопротивления качению:

(17)

Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (14) – (17):

Согласно теореме (3.2), приравниваем значения и

,

Откуда .

2.9 Задача Д4. Принцип Даламбера для механической системы

Вертикальной вал АК (рисунок Д4, таблица Д4), вращающийся с постоянной угловой скоростью ω = 10 с^-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д4 (АВ = ВД = ДЕ = ЕК = b = 0,4 м). К валу жестко прикреплены невесомый стержень 1 длиной l₁ = 0,4 м и с точечной массой m₁ = 6 кг на конце и однородный стержень 2 длиной l₂ = 0,6 м, имеющий массу m₂ = 4 кг; оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице Д4.

Пренебрегая весом вала, определить реакции подпятника и подшипника.

Таблица Д4 Данные к задаче Д4

Номер условия	Подшипник в точке	Крепление стержня 1 в точке	Крепление стержня 2 в точке	α, град	β, град
1	2	3	4	5	6
0	В	Д	К	30	45
1	Д	К	В	30	45
2	В	Д	Е	45	60
3	Е	В	К	45	30
4	Е	Д	В	60	75
5	К	Е	В	60	75
6	К	Д	Е	75	30
7	Д	Е	К	75	60
8	В	Е	Д	90	60
9	Е	К	Д	90	45

Пример Д4. Вертикальный вал длины 3а (AB = BD = DE = а), закрепленный подпятником A и подшипником E (рис. Д9б), вращается с постоянной угловой скоростью . К валу жестко прикреплен в точкеD ломаный однородный стержень массы и длины ,состоящий из двух частей 1 и 2, а в точкеB прикреплен невесомый стержень длины с точечной массойна конце; оба стержня лежат в одной плоскости.

Дано:= 15 с^-1, 10 кг,=4 кг,= 30⁰, = 120⁰, =30⁰, = 0,5 м,= 0,1 м.

Определить: реакции подпятника A и подшипника E, пренебрегая весом вала.

Указания. Задача – на применение к изучению движения системы принципа Даламбера. При решении задачи учесть, что, когда силы инерции частиц тела (в данной задаче стержня) имеют равнодействующую , то численно=ma_c, где а_с – ускорение центра масс С тела, но линия действия силы в общем случае не проходит через точку С.

Решение: Изображаем (с учетом заданных углов) вал и прикрепленные к нему в точках B и D стержни (рис. Д9а). Массы и веса частей 1 и 2 ломаного стержня пропорциональны длинам этих частей и соответственно равны

; ;;;. (1)

Для определения искомых реакций рассмотрим движение заданной механической системы и применим принцип Даламбера. Проведем вращающиеся вместе с валом оси Axy так, чтобы стержни лежали в одной плоскости xy, и изобразим действующие на систему силы: активные силы – силы тяжести и реакции связей – составляющие реакции подпятника,и реакцию цилиндрического подшипника.

Согласно принципу Даламбера, присоединим к этим силам силы инерции элементов однородного ломаного стержня и груза, считая его материальной точкой.

а) б)

Рис. Д4

Так как вал вращается равномерно, то полные ускорения элементов стержня равны нормальным ускорениям, , направлены к оси вращения и численно равны, гдеесть расстояния элементов от оси вращения. Тогда силы инерциибудут направлены от оси вращения и численно равны, где– масса элемента. Так как всепропорциональны, то эпюра этих параллельных сил инерции для части 1 стержня образует треугольник. Силы, действующие на элементы части 2 стержня, параллельны ей (рис. Д4а).

Каждую из полученных систем параллельных сил инерции заменим ее равнодействующей, равной главному вектору этих сил. Так как модуль главного вектора сил инерции любого тела имеет значение , где– масса тела,– ускорение его центра масс, то для частей стержня соответственно получим:

. (2)

Сила инерции точечной массы 3 должна быть направлена в сторону, противоположную ее ускорению, и численно равна

. (3)

Ускорения центров масс частей 1 и 2 стержня и груза 3 равны:

, (4)

где , – расстояния центров масс частей стержня от оси вращения, а – соответствующее расстояние груза:

м,

м, (5)

м.

Подсчитаем теперь по формулам (2) и (3) значения ,и:

н,

н, (6)

н.

Линия действия равнодействующей проходит через центр тяжести эпюры сил инерции части 1 стержня на расстоянии 2H/3 от вершины D треугольника, где . Линия действия равнодействующейпроходит вдоль части 2 стержня.

Согласно принципу Даламбера, приложенные внешние силы (активные и реакции связей) и силы инерции образуют уравновешенную систему сил. Составим для этой плоской системы сил три уравнения равновесия. Получим

; ,

; , (7)

;

где H₁, H₂, H₃ – плечи сил ,,относительно точкиA. Найдем численные значения этих величин, учитывая, что

м.

м, м, (8)

м.

Подставив в уравнения (7) соответствующие величины из равенств (1), (5), (6) и (8) и решив эту систему уравнений (7), найдем искомые реакции.

Ответ: Х_А=-95,0 Н; Y_A= 140,0 Н; R_E= -107,0 Н.

2.10 Задача Д5. Общее уравнение динамики

По условиям задачи Д3 определить ускорение груза 1, составив для механической системы (рисунок Д3) общее уравнение динамики. Сделать для задачи Д5отдельный чертеж.

Пример Д5. Механическая система (рис. Д11) состоит из обмотанных нитями блока 1 радиуса R₁ и ступенчатого шкива 2 (радиусы ступеней R₂ и r₂, радиус инерции относительно оси вращения ), а также из грузов 3, 4 и 5, прикрепленных к нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М₁, приложенной к блоку 1.

Дано: Р₁ = 0; Р₂= 40 Н; Р₃= 30 Н; Р₄= 20 Н; Р₅= 10 Н; М=10 Н×м; R₁ =0,2 м; R₂ = 0,3 м; r₂ = 0,15 м, = 0,2 м.

Определить: а₃ (трением пренебречь).

Указания. Задача - на применение к изучению движения системы общего уравнения динамики (принципа Даламбера - Лагранжа). Ход решения задачи такой же, как в задаче Д3, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом М^и = I_z , где I_z - момент инерции тела относительно оси вращения, - угловое ускорение тела; направление М^и противоположно направлению .

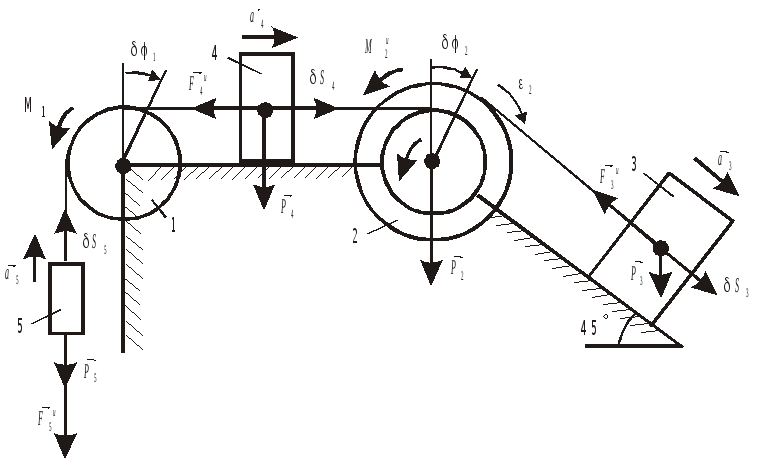
Рис. Д5

Решение: 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, …,5, соединенных нитями. Система имеет 1 степень свободы. Связи, наложенные на систему, – идеальные.

Для определения ускорения а₃ применим общее уравнение динамики:

, (1)

где – сумма элементарных работ активных сил на любом возможном перемещении системы;

–сумма элементарных работ сил инерции соответственно.

2. изображаем на чертеже активные силы: силы тяжести ,и пару сил с моментом М.

Задавшись направлением ускорения а₃, изображаем на чертеже силы инерции и пару сил с моментом, величины которых равны:

;

(2)

3. Сообщаем системе возможное перемещение и, составляя уравнение (1), получим

(3)

Выразим все возможные переменные через :

(4)

Подставим величины (2) и (4) в уравнение (3), приведем его к виду:

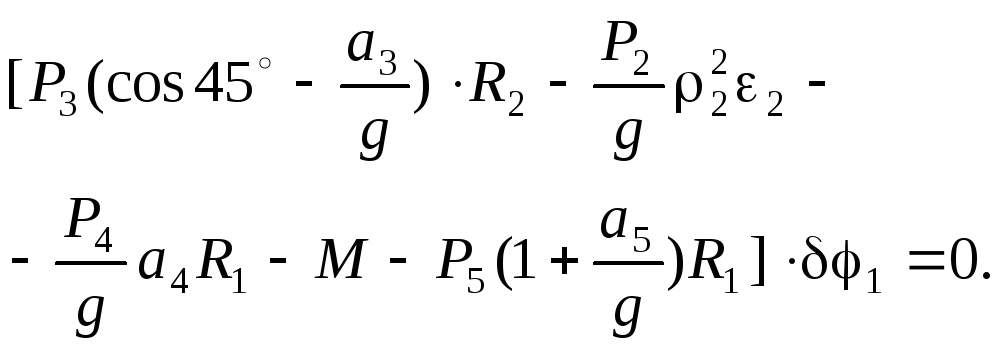(5)

Входящие сюда величины ,а₄, а₅ выразим через искомую величину а₃:

.

Затем, учтя, что , приравняем к нулю выражение, стоящее в (5) в квадратных скобках.

Из полученного уравнения найдем:

а₃ = .

Вычисления дают следующий ответ: а₃= -0,3 м/с². Знак «-» указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. Д5.

2.11 Задача Д6. Уравнения Лагранжа 2 рода

По условиям задачи Д3 определить ускорение груза 1, составив для механической системы с одной степенью свободы (рисунок Д3) уравнение Лагранжа 2 рода. По условиям задачи Д3 определить ускорение груза 1, составив для механической системы (рисунок Д3) общее уравнение динамики. Сделать для задачи Д6 отдельный чертеж.

Пример Д6. Механическая система (рис. Д3) состоит из барабана 1 радиуса R, к которому приложена пара сил с моментом М, тележки 2 и катка 3 (барабан и каток – однородные цилиндры); веса всех тел равны Р₁, Р₂, Р₃; весом колес тележки пренебречь. Тележка соединена с барабаном намотанной на него нитью, а с катком – пружиной BD, коэффициент жесткости равен с. Система начинает движение из состояния покоя; пружина в этот момент не деформирована.

Дано: P₁ = P; P₂ = P; M = 2PR.

Определить: 1) x = f(t), где x – удлинение пружины (или перемещение центра D катка по отношению к тележке); 2) частоту k и период t колебаний.

Указания. Задача – на применение к изучению движения системы уравнений Лагранжа. В задаче система имеет две степени свободы; следовательно, ее положение определяется двумя обобщенными координатами q₁ и q₂ и для нее должны быть составлены два уравнения.

Решение следует начать с выбора обобщенных координат, обозначив их q₁ =х и q₂ = илиq₁ =х и q₂ = y. За координату х принять удлинение пружины, отсчитываемое в сторону того из тел 3, 4 или 5 системы, к которому пружина прикреплена; например, если пружина прикреплена к этому телу в точке В и ее длина в произвольный момент времени равна АВ, то х = АВ – l_o, где l_o – длина недеформированной пружины. За координату j принять угол поворота крайнего блока (этот блок может быть и невесомым), отсчитывая j от начального положения. Если в систему ни один блок не входит, а входят лишь тела 3 и 4, за координату y принять расстояние тела 4 от начального положения.

Решение:

1. Для решения задачи воспользуемся уравнениями Лагранжа II рода. Рассматриваемая система имеет две степени свободы. Выберем в качестве обобщенных координат угол поворота барабана φ и удлинение пружины x (q₁ = ;q₂ = x). Тогда уравнения Лагранжа будут иметь вид:

; . (1)

2. Определим кинетическую энергию Т системы, равную сумме энергий всех тел:

Т = Т₁+Т₂+Т₃. (2)

Рис. Д6

Так как барабан вращается вокруг оси О, тележка движется поступательно, а каток – плоскопараллельно, то:

; ;, (3)

где

, .

Все входящие сюда скорости надо выразить через обобщенные скорости и. Очевидно, что,. Для определенияV_D рассмотрим движение катка как сложное. Учитывая, что x определяет положение точки D по отношению к тележке, получим , где численно. Принимая во внимание, что при возрастании φ иx скорости инаправлены в разные стороны и что точкаE для катка – мгновенный центр скоростей, получим:

, .

Подставляя все найденные значения скоростей и значения I₀ и I_D в равенства (3) и учитывая, что P₁ = P₃ = P, P₂ = 2P, получим окончательно из (2) следующее выражение для T:

. (4)

Отсюда находим:

; ;

; . (5)

3. Теперь определим обобщенные силы Q₁ и Q₂ . Изображаем действующие на систему активные силы: силы тяжести, равные ,,силы упругостии, где численно=F = cx, и пару с моментом M.

а) Для определения Q₁ сообщим системе возможное перемещение, при котором координата получает приращение, аx не изменяется, т.е. (пружина при таком перемещении системы не изменяет свою длину). Тогда тележка и центрD катка получают одинаковые перемещения и элементарная работа действующих сил будет равна:

.

Заменив здесь все величины их значениями, найдем в результате, что:

,

. (6)

б) Для определения Q₂ сообщим системе возможное перемещение, при котором координата x получает приращение , ане изменяется, т.е.(барабан не поворачивается и тележка не перемещается). Тогда работу совершает только сила.

;

. (7)

Подставляя величины (5), (6) и (7) в уравнения (1), получим следующие дифференциальные уравнения движения системы:

,

. (8)

4. Для определения исключим из уравнений (8). Получим дифференциальное уравнение вида:

,

где

, . (9)

Общее решение уравнения (9) имеет вид x = x₁+x₂, где x₁ – общее решение однородного уравнения , т.е.

.

А x₂ – частное решение уравнения (9), которое будем искать в виде x₂ = A = const. Подставляя x₂ в (9), получим . Таким образом, общее решение уравнения (9) имеет вид:

. (10)

Продифференцировав уравнение (10), получим:

. (11)

По начальным условиям при t = 0, x = 0, (движение начинается из состояния покоя и пружина в этот момент не деформирована).

Подставляя эти величины в уравнение (10) и в уравнение (11), найдем из них, что ,.

Окончательно получаем искомую зависимость x = f(t) в виде:

, (12)

где значения a и k² даются последними двумя равенствами из (9). Таким образом, центр катка D совершает по отношению к тележке колебания, закон которых дает равенство (12). Частота k и период этих колебаний:

; . (13)

Контрольные вопросы для самопроверки:

Раздел Статика

1. Основные исторические этапы развития теоретической механики.

2. Сила, система сил, эквивалентная система сил и уравновешенная

система сил.

3. Аксиомы статики и следствия из них.

4. Принцип освобождаемости от связей (аксиома связей).

5. Исследование связей и установление направления их реакций.

6. Геометрический метод определения равнодействующей

пространственной и плоской систем сходящихся сил.

7. Условие равновесия пространственной и плоской систем сходящихся сил в геометрической форме.

7. Проекция силы на ось и на плоскость.

8. Определение силы по ее проекциям на координатные оси.

9. Аналитический метод определения равнодействующей

пространственной и плоской систем сил.

10. Условия равновесия пространственной и плоской систем сходящихся сил в аналитической форме.

10. Момент силы относительно точки.

11. Теорема Вариньона о моменте равнодействующей.

12. Приведение системы двух параллельных сил, направленных в одну сторону, к равнодействующей.

13. Приведение системы двух не равных по модулю параллельных сил, направленных в противоположные стороны, к равнодействующей.

14. Пара сил. Момент пары сил.

15. Эквивалентность пар сил.

16. Сложение пар сил, расположенных в одной плоскости. Условие равновесия пар.

17. Теорема о параллельном переносе силы.

18. Приведение произвольной плоской системы сил к одной силе и к одной паре.

19. Приведение произвольной плоской системы сил к равнодействующей.

20. Теорема Вариньона о моменте равнодействующей произвольной плоской системы сил. Условие равновесия рычага.

21. Условия равновесия произвольной плоской системы сил.

22. Условия равновесия плоской системы параллельных сил.

23. Равновесие сочлененной системы тел.

24. Трение скольжения. Конус трения.

25. Трение качения. Коэффициент трения качения. Момент трения качения.

26. Понятие о ферме. Способ вырезания узлов.

27. Способ сечений фермы.

28. Момент силы относительно точки как вектор.

29. Момент силы относительно оси.

30. Зависимость между моментом силы относительно оси и моментом силы относительно точки, лежащей на этой оси.

31. Аналитическое выражение моментов силы относительно координатных осей.

32. Сложение пар, лежащих в разных плоскостях.

33. Приведение произвольной пространственной системы сил к одной силе и к одной паре.

34. приведение произвольной пространственной системы сил к динамическому винту.

35. Условия равновесия произвольной пространственной системы сил.

36. Условия равновесия пространственной системы параллельных сил.

37. Центр тяжести.

38. Определение центра тяжести площади треугольника.

39. Центр тяжести площади кругового сектора.

Раздел кинематика

1. Три способа задания движения точки.

2. Векторный способ задания движения точки. Мгновенная скорость

точки. Ускорение точки.

3. Годограф вектора скорости точки.

4. Координатный способ задания движения точки. Определение

скорости и ускорения точки.

5. Естественный способ задания движения точки. . Определение

скорости и ускорения точки.

6. Определение скорости и ускорения точки при естественном способе задания ее движения.

7. Частные случаи движения точки по прямой и по окружности. Определение скорости и ускорения точки.

8. Простейшие движения твердого тела.

9. Поступательное движение твердого тела.

10. Вращение твердого тела вокруг неподвижной оси.

11. Определение скорости и ускорения точки твердого тела. вращающегося вокруг неподвижной оси.

12. Сложное движение точки. Относительное, переносное и абсолютное движения точки.

13. Теорема сложения скоростей при сложном движении точки.

14. Теорема сложения ускорений при поступательном переносном движении.

15. Теорема сложения ускорений при вращательном переносном движении.

16. Ускорение Кориолиса. Определение величины и направления.

17.Уравнения плоскопараллельного движения твердого тела.

18. Разложение движения плоской фигуры на поступательное и вращательное.

19. Определение скоростей точек плоской фигуры, движущейся в своей плоскости.

20. Теорема о проекциях скоростей двух точек плоской фигуры на прямую, соединяющую эти точки.

21. Мгновенный центр скоростей плоской фигуры.

22. Определение ускорений точек плоской фигуры, движущейся в своей плоскости.

23. Мгновенный центр ускорений точек плоской фигуры.

24. Теоремы о сложении вращений твердого тела вокруг неподвижных осей.

25. Теоремы от сложении поступательного и вращательного движений твердого тела.

Раздел динамика

1. Раздел теоретической механики – динамика. Две задачи динамики.

2. Основные законы динамики.

3. Дифференциальные уравнения движения свободной материальной

точки

4. Дифференциальные уравнения движения несвободной материальной точки.

5. Принцип Даламбера для материальной точки.

6. Дифференциальные уравнения движения материальной точки.

7. Гармонические колебания материальной точки.

8. Затухающие колебания материальной точки.

9. Вынужденные колебания материальной точки при отсутствии сопротивления.

10. Вынужденные колебания материальной точки при наличии сопротивления.

11. Механическая система. Классификация сил, действующих на механическую систему.

12. Масса системы. Центр масс механической системы.

13. Моменты инерции твердого тела относительно точки, оси и

плоскости

14. Определение момента инерции тонкого однородного стержня.

15. Момент инерции однородного кольца или обруча.

16. Момент инерции круглого тонкого однородного диска.

17. Момент инерции круглого однородного цилиндра.

18. Теорема Гюйгенса.

19. Дифференциальные уравнения движения механической системы.

20. Теорема об изменении количества движения точки.

21. Теорема об изменении количества движения механической системы.

22. Закон сохранения количества движения механической системы.

23. Теорема о движении центра масс механической системы.

24. Теорема об изменении кинетического момента точки.

25. Теорема об изменении кинетического момента механической

системы.

26. Закон сохранения кинетического момента механической системы.

27. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси.

28. Теорема об изменении кинетической энергии материальной точки.

29. Элементарная работа силы.

30. Вычисление работы и мощности силы, приложенной к материальной точке.

31. Определение работы силы тяжести.

32. Определение работы силы упругости.

33. Теорема об определении кинетической энергии механической системы.

34. Определение кинетической энергии твердого тела, движущегося поступательно.

35. Определение кинетической энергии твердого тела, вращающегося вокруг неподвижной оси.

37. Определение кинетической энергии твердого тела при плоскопараллельном движении.

38. Потенциальное силовое поле.

39. Дифференциальные уравнения плоскопараллельного движения твердого тела.

40. Принцип Даламбера для механической системы.

41. Определение динамических реакций в точках закрепления вращающегося тела.

42. Классификация связей.

43. Возможные перемещения механической системы.

44. Понятие работы сил на возможном перемещении. Обобщенная сила. Идеальные связи.

45. Принцип возможных перемещений.

46. Общее уравнение динамики.

47. Дифференциальные уравнения движения системы в обобщенных координатах.

48. Явление удара. Ударная сила и ударный импульс.

49. Основное уравнение теории удара.

50. Теорема об изменении количества движения системы при ударе.

51. Условия, при которых удар не передается на точки закрепления оси. Центр удара.

52. Прямой центральный удар тела о неподвижную преграду.

53. Случай косого удара шара о неподвижную преграду.

54. Прямой центральный удар двух тел.

55. Потеря кинетической энергии при прямом центральном ударе двух тел. Теорема Карно.