Решение.

1. Статическая сторона задачи.

С учетом симметрии относительно оси Yимеем:

,

отсюда (a)

2. Геометрическая сторона задачи.

В результате термического расширения точка А переместится в А₁(рис. 2.52, б). Исходя из схемы деформированной конструкции можно составить условие совместности деформаций:

(b)

3. Физическая сторона задачи.

Крайние стержни 1 длиннее среднего стержня 2; кроме того, у край­них стержней коэффициент линейного расширения больше, чем у сред­него. По этой причине точка А у первых стержней опустилась бы ниже, чем точка А у второго стержня, если бы они деформировались отдельно. Но так как они в точке А связаны шарниром, то возникает силовое взаи­модействие боковых и среднего стержней. Боковые стержни, удлиняясь за счет термического воздействия, будут одновременно укорачиваться в результате действия возникающего усилия, средний же стержень будет удлиняться как за счет термического расширения, так и за счет механи­ческого действия на него крайних стержней.

Следовательно

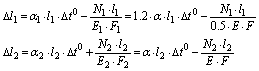(c)

где

подставляя (с) в (б), получим:

(d)

4. Определение неизвестных.

Решая систему уравнений (а) и (d) с учетом, чтоR₁=N₁иR₂=N₂, получим:

 

Пример 25.

Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 2.53). Исходные данные: а= 2,1 м,b= 2,4 м,с= 1,5 м,F= 12см², Е = 2·10⁵МПа.

Требуется найти:

1. усилия и напряжения в стержнях, выразив их через силу Q;

2. допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению= 160 МПа;

3. предельную грузоподъемность системы Q_пр.и допускаемую нагрузку [Q_пр], если предел текучести= 240 МПа и запас прочностиn= 1,5;

4. сравнить величины допускаемых нагрузок [Q] и [Q_пр].

Рис.2.53

 

Решение.

Усилия N₁, иN₂в стержняхАА₁, иВВ₁, шарнирно прикрепленных по концам, направлены вдоль осей этих стержней. Реакция опорыКимеет горизонтальную составляющуюН_К, и вертикальную составляющуюR_К, т.к. эта опора препятствует горизонтальному и вертикальному перемещению точкиКбруса.

Таким образом, всего имеется четыре неизвестные реакции (рис.2.54), а уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима. Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи.

Рис. 2.54

 

1. Найдем усилия и напряжения в стержнях, выразив их через силу Q.

Статическая сторона задачи. По условию задачи необходимо определить усилия N₁, иN₂стальных стержнейАА₁, иВВ₁,aв определений реакцийН_К, иR_Кнет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакцияН_К, иR_К. Таким является уравнение в виде суммы моментов всех сил относительно шарнираК:

,

где м.

Подставляя в уравнение значения h,b,с, получим

.(а)

 

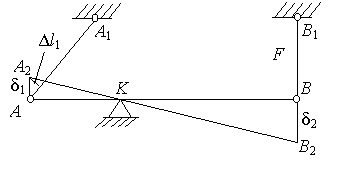
Рис.2.55

 

Геометрическая сторона задачи.Под действием внешней силыQабсолютно жесткий брус повернется вокруг точкиК. ШарнирыАиВпосле деформации переходят в положениеА₂иВ₂соответственно, т.е. перемещаются по вертикали на величиныи(рис.2.55).

Из подобия треугольников AA₂КиВВ₂Кнаходим

.(b)

Выразим укорочение стержняАА₁и удлинениестержняВB₁, через перемещенияи.

,,

откуда

или с учетом равенства (b)

(c)

Физическая сторона задачи.Используя закон Гука, записанный для абсолютных деформаций, выразим удлинения стержней через усилия

;

; (d)

Подставим выражения (c) в условие (d)

,

после сокращения получим

(e)

Решаем совместно уравнения статики (a) и уравнение (e):

.

Определяем напряжения в стержнях 1 и 2:

Па,

Па.

2. Найдем допускаемую нагрузку [Q], приравняв большее из напряжений в двух стержнях допускаемому напряжению= 160 МПа.

,

откуда

Н.

3. Найдем предельную грузоподъемность системы Q_пр.и допускаемую нагрузку [Q_пр], если предел текучести= 240 МПа и запас прочностиn= 1,5.

При увеличении нагрузки Qcверх значения [Q] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величинынапряжениево второй стержне достигают предела текучести, а усилиеN₂- предельного значенияN_2пр=c₁·F. При этом напряжениев первом стержне остается меньше. В процессе дальнейшего увеличения нагрузки напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом - возрастают, пока также не становятся равными, усилиеN₁при этом равно. Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. ВеличинуQ, вызываюшую предельное состояние, обозначаютQ_при называют предельной нагрузкой.

Для определения Q_пр, подставим в уравнение (a) значения сил, соответствующих предельному состоянию, когдаQ=Q_пр,N₁=N_1пр,N₂=N_2пр:

,

откуда

Н.

Н.

4. Сравним величины допускаемых нагрузок [Q] и [Q_пр]

.

Следовательно, при расчете на прочность данной системы по предельной нагрузке грузоподъемность ее увеличивается на 38%.

 

Расчет конструкций по допускаемым нагрузкам.

Расчет статически определимых систем по способу допускаемых нагрузок.

   В предыдущем изложении методов расчета мы исходили из основного условия прочности . Это неравенство требует выбора размеров конструкции с таким расчетом, чтобы наибольшее напряжение в самом опасном месте не превосходило допускаемого.

   Но можно стать на другую точку зрения. Можно задать условие, чтобы действительная нагрузка на всю конструкцию не превосходила некоторой допускаемой величины. Условие это можно выразить таким неравенством:

За допускаемую нагрузку надо выбрать некоторую часть той нагрузки, при которой конструкция перестанет функционировать правильно, перестанет выполнять свое назначение. Такая нагрузка обычно называетсяпредельной, иногда—разрушающей в широком смысле слова (под разрушением конструкции подразумевают прекращение ее нормальной работы).

В качестве примера возьмем систему из двух стальных стержней АВ и АС (рис.2.56), нагруженных силой P.

 

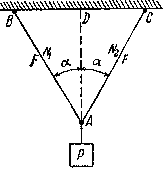Рис.2.56

 

 Рассчитывая эту систему обычным путем, найдем усилия N₁ = N₂ no формуле:

(из равновесия узла А). Отсюда площадь каждого из стержней равна:

По способу допускаемых нагрузок имеем:

Введя в качестве коэффициента запаса для конструкции в целом ту же величину k, которая была принята в качестве коэффициента запаса для напряжений, мы получим, что величина

Предельной, опасной величиной P_пр будет та, при которой напряжения в стержнях дойдут до предела текучести:

Таким образом, допускаемая величина Р равна:

Условие прочности принимает вид

а учитывая, что

,

получаем:

Отсюда:

Таким образом, расчет по допускаемым нагрузкам привел в данном случае к тем же результатам, что и расчет по допускаемым напряжениям. Это всегда имеет место для статически определимых конструкций при равномерном распределении напряжений, когда материал по всему сечению используется полностью.

 

Расчет статически неопределимых систем по способу допускаемых нагрузок

Совсем другие результаты мы получим, если будем применять способ допускаемых нагрузок к статически неопределимым системам, стержни которых изготовлены из материала, обладающего способностью к большим пластическим деформациям, например из малоуглеродистой стали.

В качестве примера рассмотрим систему из трех стержней, нагруженных силой Q (рис. 2.57). Пусть все стержни сделаны из малоуглеродистой стали с пределом текучести . Длины крайних стержней, как и выше, обозначим; длину среднего. Допускаемое напряжение.

 

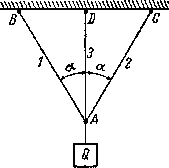Рис.2.57

 

Как и раньше, при расчете этой статически неопределимой системы зададимся отношением площадей стержней; примем, что все три стержня будут иметь одинаковую площадь F. Получим:

1.

2.

3. .

Используя закон Гука, получим:

Следовательно:

Так как , средний стержень напряжен больше, чем крайние; поэтому подбор площади сечения F надо произвести по формуле:

Ту же величину площади надо дать и боковым стержням; в них получается некоторый дополнительный запас.

Применим способ допускаемых нагрузок; условием прочности будет:

Что в данном случае следует понимать под предельной нагрузкой конструкции? Так как конструкция выполнена из материала, имеющего площадку текучести, то, по аналогии с простым растяжением стержня из такого материала, за предельную нагрузку следует взять груз, соответствующий достижению состояния текучести для всей конструкции в целом. Назовем эту нагрузку . Пока силаQ не достигла этого значения, для дальнейшей деформации (опускания точки A) требуется возрастание нагрузки. Когда же Q сделается равным , дальнейший рост деформаций будет происходить уже без увеличения нагрузки, — конструкция выйдет из строя.

Для определения величины рассмотрим постепенный ход деформации нашей стержневой системы. Так как средний стержень напряжен сильнее крайних, то в нем раньше, чем в других, напряжение дойдет до предела текучести. Нагрузку, соответствующую этому моменту, обозначимQ_Т; она будет равна:

где — усилие в среднем стержне, соответствующее его пределу текучести.

Напряжения в крайних стержнях, имеющих ту же площадь, в этот момент еще не дойдут до предела текучести, и эти стержни будут упруго сопротивляться дальнейшей деформации. Для того чтобы эта деформация происходила, необходимо дальнейшее увеличение нагрузки до тех пор, пока в крайних стержнях напряжения тоже не дойдут до предела текучести. Лишь тогда будет достигнута предельная грузоподъемность конструкции .

Так как при нагрузке Q_Т напряжения в среднем стержне дойдут уже до предела текучести , то при дальнейшем возрастании груза они, а стало быть и усилиеN₃, останутся без увеличения. Наша статически неопределимая система превратится в статически определимую, состоящую из двух стержней АВ и АС и нагруженную в точке А силой Q, направленной вниз, и известным усилием , равным(рис.2.58).

 

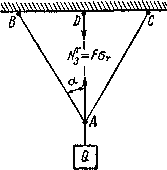Рис.2.58

 

Такая схема работы нашей конструкции будет иметь место, пока

Для иллюстрации хода деформации рассматриваемой конструкции изобразим графически зависимость между силой Q и перемещением f точки А (рис. 2.59). Пока опускание точкиА равно удлинению среднего стержня и определяется формулой

.

 

Рис.2.59

 

Как только Q будет заключаться в промежутке перемещение точкиА должно быть вычислено, как опускание этого узла в системе двух стержней АС и АВ, нагруженных в точке А силой . Так как:

и, в свою очередь:

;

Отсюда

;

Для f₁₂ (на втором участке) получаем уравнение прямой, но уже не проходящей через начало координат. После достижения нагрузкой Q значения напряжения в крайних стержнях достигнут предела текучести, и система будет деформироваться без увеличения нагрузки. График перемещения идет теперь параллельно оси абсцисс.

Для определения предельной грузоподъемности всей системы мы должны для системы двух стержней, нагруженных силой , найти то значение Q, при котором напряжения и в крайних стержнях дойдут до предела текучести. Такая задача решена в предыдущем параграфе; подставляя в выражение (а) вместо Р величину , получаем:

Отсюда

Допускаемая нагрузка будет равна

а учитывая, что

,

получаем

Окончательно:

и

Эта величина меньше, чем полученная обычным методом расчета, т. е.

При (сталь) получаем: по обычному способу

по способу допускаемых нагрузок:

Таким образом, метод расчета по допускаемым нагрузкам позволяет спроектировать статически неопределимую систему из материала, обладающего площадкой текучести, экономичнее, чем при расчете по допускаемым, напряжениям. Это понятно: при способе расчета по допускаемым напряжениям мы считали за предельную нагрузку нашей конструкции величину Q_Т, при которой до предела текучести доходил лишь материал среднего стержня, крайние же были недонапряжены. При методе расчета по допускаемым нагрузкам предельная грузоподъемность определяется величиной . При нагрузкеполностью используется материал всех трех стержней.

Таким образом, новый метод расчета позволяет реализовать скрытые при старом способе запасы прочности в статически неопределимых системах, добиться повышения их расчетной грузоподъемности и действительной равнопрочности всех частей конструкции. Не представит никаких затруднений распространить этот метод на случай, когда соотношение площадей среднего и крайних стержней не будет равно единице.

Изложенные выше теоретические соображения проверялись неоднократно на опыте, причем всегда наблюдалась достаточно близкая сходимость величин предельной нагрузки — вычисленной и определенной при эксперименте. Это дает уверенность в правильности теоретических предпосылок метода допускаемых нагрузок.

 

Расчет гибких нитей

В технике встречается еще один вид растянутых элементов, при определении прочности которых важное значение имеет собственный вес. Это — так называемые гибкие нити. Таким термином обозначаются гибкие элементы в линиях электропередач, в канатных дорогах, в висячих мостах и других сооружениях.

Пусть (рис.2.60) имеется гибкая нить постоянного сечения, нагруженная собственным весом и подвешенная в двух точках, находящихся на разных уровнях. Под действием собственного веса нить провисает по некоторой кривой АОВ.

Горизонтальная проекция расстояния между опорами (точками ее закрепления), обозначаемая , носит названиепролета.

Нить имеет постоянное сечение, следовательно, вес ее распределен равномерно по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, и длина кривой АОВ мало отличается (не более чем на 10%) от длины хорды АВ. В этом случае с достаточной степенью точности можно считать, что вес нити равномерно распределен не по ее длине, а по длине ее проекции на горизонтальную ось, т. е. вдоль пролета l.

 

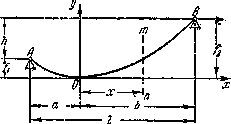Рис.2.60

 

Эту категорию гибких нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равномерно распределенной по пролету нити, равна q. Эта нагрузка, имеющая размерность сила/длина, может быть не только собственным весом нити, приходящимся на единицу длины пролета, но и весом льда или любой другой нагрузкой, также равномерно распределенной. Сделанное допущение о законе распределения нагрузки значительно облегчает расчет, но делает его вместе с тем приближенным; если при точном решении (нагрузка распределена вдоль кривой) кривой провисания будет цепная линия, то в приближенном решении кривая провисания оказывается квадратной параболой.

Начало координат выберем в самой низшей точке провисания нити О, положение которой, нам пока неизвестное, очевидно, зависит от величины нагрузки q, от соотношения между длиной нити по кривой и длиной пролета, а также от относительного положения опорных точек. В точке О касательная к кривой провисания нити, очевидно, горизонтальна. По этой касательной направим вправо ось .

Вырежем двумя сечениями — в начале координат и на расстоянии от начала координат (сечениеm — n) — часть длины нити. Так как нить предположена гибкой, т. е. способной сопротивляться лишь растяжению, то действие отброшенной части на оставшуюся возможно только в виде силы, направленной по касательной к кривой провисания нити в месте разреза; иное направление этой силы невозможно.

   На рис.2.61 представлена вырезанная часть нити с действующими на нее силами. Равномерно распределенная нагрузка интенсивностью q направлена вертикально вниз. Воздействие левой отброшенной части (горизонтальная сила Н) направлено, ввиду того, что нить работает на растяжение, влево. Действие правой отброшенной части, сила Т, направлено вправо по касательной к кривой провисания нити в этой точке.

Cоставим уравнение равновесия вырезанного участка нити. Возьмем сумму моментов всех сил относительно точки приложения силы Т и приравняем ее нулю. При этом учтем, опираясь на приведенное в начале допущение, что равнодействующая распределенной нагрузки интенсивностью q будет , и что она приложена посредине отрезка. Тогда

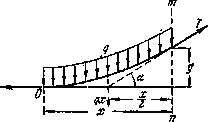Рис.2.61

 

 ,

откуда

(2.39)

Отсюда следует, что кривая провисания нити является параболой. Когда обе точки подвеса нити находятся на одном уровне, то . Величинав данном случае будет так называемой стрелой провисания. Ее легко определить. Так как в этом случае, ввиду симметрии, низшая точка нити находится посредине пролета, то; подставляя в уравнение (2.39) значенияиполучаем:

(2.40)

Из этой формулы находим величину силы Н:

(2.41)

Величина Н называется горизонтальным натяжением нити.

Таким образом, если известны нагрузка q и натяжение H, то по формуле (2.40) найдем стрелу провисания . Призаданных инатяжениеН определяется формулой (2.41). Связь этих величин с длиной нити по кривой провисания устанавливается при помощи известной из математики приближенной формулы)

Составим еще одно условие равновесия вырезанной части нити, а именно, приравняем нулю сумму проекций всех сил на ось :

Из этого уравнения найдем силу Т — натяжение в произвольной точке

Откуда следует, что сила Т увеличивается от низшей точки нити к опорам и будет наибольшей в точках подвеса — там, где касательная к кривой провисания нити составляет наибольший угол с горизонталью. При малом провисании нити этот угол не достигает больших значений, поэтому с достаточной для практики степенью точности можно считать, что усилие в нити постоянно и равно ее натяжению Н. На эту величину обычно и ведется расчет прочности нити. Если все же требуется вести расчет на наибольшую силу у точек подвеса, то для симметричной нити ее величину определим следующим путем. Вертикальные составляющие реакций опор равны между собой и равны половине суммарной нагрузки на нить, т. е. . Горизонтальные составляющие равны силеН, определяемой по формуле (2.41). Полные реакции опор получатся как геометрические суммы этих составляющих:

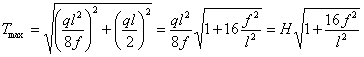
Условие прочности для гибкой нити, если через F обозначена площадь сечения, имеет вид:

Заменив натяжение Н его значением по формуле (2.41), получим:

   Из этой формулы при заданных ,,иможно определить необходимую стрелу провисания. Решение при этом упростится, еслив включен лишь собственный вес; тогда, где— вес единицы объема материала нити, и

т. е. величина F не войдет в расчет.

Если точки подвеса нити находятся на разных уровнях, то, подставляя в уравнение (2.39) значения и, находими:

Отсюда из второго выражения определяем натяжение

а деля первое на второе, находим:

или

Имея в виду, что , получаем:

или

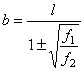
Подставив это значение в формулу определенного натяженияН, окончательно определяем:

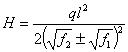(2.42)

Два знака в знаменателе указывают на то, что могут быть две основные формы провисания нити. Первая форма при меньшем значении Н (знак плюс перед вторым корнем) дает нам вершину параболы между опорами нити. При большем натяжении Н (знак минус перед вторым корнем) вершина параболы расположится левее опоры А. Получаем вторую форму кривой. Возможна и третья (промежуточная между двумя основными) форма провисания, соответствующая условию ; тогда начало координатсовмещается с точкойА. Та или иная форма будет получена в зависимости от соотношений между длиной нити по кривой провисания АОВ (рис.2.60) и длиной хорды АВ.

Если при подвеске нити на разных уровнях неизвестны стрелы провисания и, но известно натяжениеН, то легко получить значения расстояний а и b и стрел провисания и. Разностьh уровней подвески равна:

Подставим в это выражение значения и, и преобразуем его, имея в виду, что:

откуда

а так как то

и

 Следует иметь в виду, что при будет иметь место первая форма провисания нити,при — вторая форма провисания и при— третья форма. Подставляя значенияив выражения для стрел провисанияи, получаем величиныи:

Теперь выясним, что произойдет с симметричной нитью, перекрывающей пролет , если после подвешивания ее при температуреи интенсивности нагрузкитемпература нитиповысится до а нагрузка увеличится до интенсивности(например, из-за ее обледенения). При этом предположим, что в первом состоянии задано или натяжение, или стрела провисания(Зная одну из этих двух величин, всегда можно определить другую.)

При подсчете деформации нити, являющейся по сравнению с длиной нити малой величиной, сделаем два допущения: длина нити равна ее пролету, а натяжение постоянно и равно Н. При пологих нитях эти допущения дают небольшую погрешность.

В таком случае удлинение нити, вызванное увеличением температуры, будет равно

где — коэффициент линейного температурного расширения материала нити.

При повышении температуры нить удлиняется. В связи с этим увеличится ее стрела провисания и, как следствие, уменьшится ее натяжение. С другой стороны, из-за увеличения нагрузки, как видно из формулы (2.41), натяжение увеличится. Допустим, что окончательно натяжение увеличивается. Тогда удлинение нити, вызванное увеличением натяжения, будет, согласно закону Гука, равно:

Если окажется меньше, чем то величинабудет отрицательной. При понижении температуры будет отрицательной величина.

   Таким образом, длина нити во втором ее состоянии будет равна длине при первом ее состоянии с добавлением тех деформаций, которые произойдут от повышения температуры и натяжения:

Изменение длины нити вызовет изменение и ее стрелы провисания. Вместо , она станет.

Теперь заменим в последнем уравнении иих известными выражениями, а деформациии— также их полученными ранее значениями. Тогда уравнение дляS₂ примет следующий вид:

В этом уравнении заменим иих значениями по формуле (2.40):

и

Тогда, после некоторых преобразований, уравнение для расчета натяжения может быть написано в виде:

Определив из этого уравнения натяжение , можно найти по формуле (2.40) и стрелу.

В случае, если при переходе от первого ко второму состоянию нагрузка не изменяется, а изменяется лишь температура, то в последнем уравнении интенсивность заменяется на. В случае, если при переходе от первого ко второму состоянию не изменяется температура, а изменяется лишь нагрузка, то в этом уравнении средний член в квадратной скобке равен нулю. Полученное уравнение пригодно, конечно, и при понижении температуры и уменьшении нагрузки.

В тех случаях, когда стрела провисания не является малой по сравнению с пролетом, выведенные выше формулы, строго говоря, неприменимы, так как действительная кривая провисания нити, цепная линия, будет уже значительно отличаться от параболы, полученной нами благодаря предположению о равномерном распределении нагрузки по пролету нити, а не по ее длине, как то имеет место в действительности.

Точные подсчеты показывают, что значение погрешности в величине натяжения Н, вызванной этим предположением, таково: при отношении погрешность не превосходит 0,3%,при ошибка составляет уже 1,3%, а припогрешность несколько, превосходит 5%.