1. Цель работы

В процессе выполнения лабораторного практикума студент должен освоить:

• элементы математического аппарата цифровой техники;

• функции алгебры логики;

• анализ и синтез комбинационных цифровых устройств;

• метод упрощения выражений для функций алгебры логики с помощью карт Карно;

• минимизация заданной логической функции с применением средств

вычислительной техники;

- программную модель микропроцессора (МП);

- команды МП;

- принципы выполнения вычислений МП.

2. Теоретическая часть

2.1 Системы счисления.

Система изображения любых чисел с помощью ограниченного числа символов называется системой счисления. Используемые в системе счисления символы называются цифрами.

Существуют различные системы счисления, и от их особенностей зависит наглядность представления числа при помощи цифр и сложность выполнения арифметических операций. Если в системе счисления каждой цифре в любом месте числа соответствует одно и то же значение — количественный эквивалент, то такая система счисления называется непозиционной. Таким образом, для непозиционных систем счисления местоположение цифры в записи числа не играет никакой роли. Примером непозиционной системы счисления является римская система, в которой используются римские цифры I, V, X, L, С, М. Соответственно значение числа, например, CCXXIV вычисляется следующим образом: С=100, Х=10, V=5, 1 = 1. При этом вес цифры не зависит от ее местоположения в записи числа, а знак зависит. Если цифра с меньшим весом стоит слева от цифры с большим весом, то ее знак «—», а если цифра с меньшим весом стоит справа от цифры с большим весом, то ее знак «+». Общим недостатком непозиционных систем счисления являются трудности записи в таких системах больших чисел и трудности выполнения арифметических операций, поскольку для этого используются громоздкие правила. Поэтому в цифровой технике непозиционные системы практически не нашли применения.

В цифровой технике используются позиционные системы счисления. Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее позицией в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции цифры по некоторому закону. В позиционных системах число

будет равно сумме

где — символы, обозначающие целые числа;

—веса, т.е. количественные значения каждой единицы, определяемые местом соответствующего символа в изображении числа. При изображении разных чисел в любой конкретной системе счисления символы

могут менять свое цифровое выражение, но веса единиц, расположенных на одних и тех же позициях во всех числах, сохраняют одно и то же заранее обусловленное значение. Номер позиции, который определяет вес единицы, расположенной на этой позиции, называется разрядом.

Среди позиционных систем особое значение имеют системы счисления, в которых вес отдельных разрядов представляет собой ряд членов геометрической прогрессии со знаменателем р. В этом случае число

будет иметь значение

В этой последовательности запятая определяет целую часть числа от дробной, т.е. коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях. Запятая опускается, если нет отрицательных степеней. Число различных символов — цифр, необходимых для записи произвольного числа, равно знаменателю геометрической прогрессии р. В большинстве случаев используются числа натурального ряда 0, 1, 2, ..., (р—1). Знаменатель геометрической прогрессии р, равный отношению веса любого разряда к весу соседнего справа разряда, называется основанием системы счисления. Соответственно количество цифр, употребляемых в позиционной системе счисления, равно ее основанию.

В десятичной системе основание р = 10 и для записи чисел используется десять цифр: 0, 1,2,...,9. Каждая цифра числа занимает в нем определенный разряд, который имеет весовые коэффициенты для разрядов влево от запятой

10⁰, 10¹, 10²,... и вправо от запятой10^-1, 10^-2, 10^-3,... Таким образом, запись 547,359 в десятичной системе счисления означает следующее количество:

547,359 = 5•10² + 4•10¹ + 7•10° + 3•10^-1 + 5•10^-2 + 9•10^-3.

Позиционные системы счисления имеют ряд преимуществ перед непозиционными. Основным преимуществом следует считать удобство выполнения таких арифметических операций, как сложение, вычитание, умножение, деление, извлечение корня и др. Поэтому в цифровой технике, как правило, применяются позиционные системы счисления. Выбор основания системы счисления зависит от физических элементов, на основе которых строится то или иное устройство. В цифровой технике широко используются элементы с двумя устойчивыми состояниями. В этих элементах различие между отдельными фиксированными состояниями носит качественный, а не количественный характер, благодаря чему представление чисел с их помощью может быть реализовано значительно надежнее, чем с помощью элементов, в которых число четко различимых состояний превышает два. В частности, выполнение элемента с десятью четко различимыми состояниями представляет собой сложную техническую задачу. Указанное обстоятельство явилось одной из главных причин распространения в цифровой технике позиционных систем с недесятичным основанием, в первую очередь двоичной, а также восьмеричной и шестнадцатеричной систем счисления.

Наибольшее распространение в цифровой технике имеет двоичная система счисления. В этой системе используются только две цифры: 0 и 1. В двоичной системе любое число может быть представлено последовательностью двоичных цифр:

где а_і принимает значение либо 0, либо 1. Эта запись соответствует сумме степеней числа два, взятых с указанными в ней коэффициентами

Вес разрядов, отсчитываемых влево от запятой, в целой части числа равен соответственно 1, 2, 4, 8, 16, ..., вес же разрядов правее запятой в дробной части будет ½, ¼, ¹/₈, ¹/₁₆. Например, число 11010,11₂ соответствует следующему количеству:

которое, как следует из приведенного разложения его по степеням числа 2, равно десятичному числу 26,75₁₀. В восьмеричной системе счисления употребляется восемь цифр: 0, 1,2, ..., 7. Любое число в восьмеричной системе представляется последовательностью в которой цифры могут принимать значения от 0 до 7. Вес разрядов целой части 1, 8, 64, 256, ..., в дробной части ¹/₈, ¹/₆₄, ¹/₂₅₆. Например, восьмеричное число 756,25

равно десятичному числу 494, 328125₁₀.

В шестнадцатеричной системе счисления для изображения чисел употребляется 16 цифр: 0...15. При этом чтобы одну цифру не изображать двумя символами, приходится вводить специальные обозначения для цифр больше девяти. В качестве шести символов обычно используются буквы латинского алфавита: А, В, С, D, E, F, которым в десятичной системе соответствуют числа 10, 11, 12, 13, 14, 15. Таким образом, шестнадцатеричное число А7В,C8₁₆ соответствует следующему количеству:

равному десятичному числу 2683,78125₁₀.

2.2 Перевод чисел из одной системы счисления в другую.

Правила перевода чисел из двоичной системы в восьмеричную, шестнадцатеричную и обратно достаточно просты, поскольку основания восьми- и шестнадцатеричной систем счисления выражаются целой степенью двух (8=2³, 16=2⁴). Для перевода чисел из восьмеричной системы в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом — триадой. Например:

Перевод шестнадцатеричных чисел в двоичную систему счисления осуществляется представлением цифр шестнадцатеричного числа четырехразрядными двоичными числами — тетрадами. Например,

При обратном переводе чисел из двоичной системы в восьми- и шестнадцатеричную системы необходимо разряды двоичного числа, отсчитывая от запятой влево и вправо, разбить на группы по три разряда при переводе в восьмеричную систему или в группы по четыре разряда при переводе в шестнадцатеричную систему. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представляется цифрой той же системы счисления, в которую переводится число. Например,

В общем случае, при некратных основаниях, перевод числа, содержащего целую и дробную части,

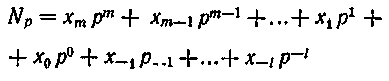
из системы с основанием p₁ в систему с основанием р₂ можно выполнить по универсальному алгоритму, при котором целая и дробная части приводятся к следующему виду:

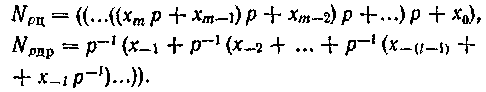
Согласно этому алгоритму перевод числа состоит из вычислительных процессов двух видов:

• последовательного деления целой части и образующихся целых частных на основание новой системы счисления,

• 2) последовательного умножения дробной части и дробных частей получающихся произведений на то же новое основание, записанное, как и в первом случае, цифрами исходной системы счисления.

При переводе целой части числа остатки, получающиеся в результате процесса последовательного деления, представляют цифры а₀, а₁,... целой части числа в новой системе счисления, записанные цифрами исходной системы счисления. Последний остаток является старшей цифрой переведенного числа.

При переводе дробной части числа целые части, получающиеся при каждом умножении, не участвуют в последующих умножениях. Они представляют цифры в дробной части исходного числа в новой системе счисления, изображенные цифрами исходной системы. Значение первой целой части является первой цифрой после запятой переведенного числа.

При преобразовании десятичных чисел в двоичные целая часть должна последовательно делиться на 2, а дробная часть — умножаться на 2. Например, при переводе десятичного числа 30,6 в двоичное получим целую часть путем деления:

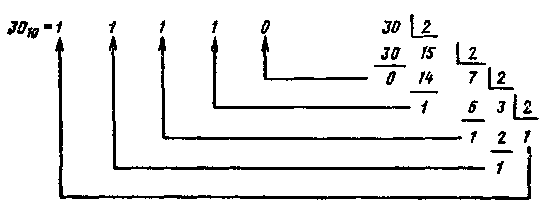
и дробную часть путем умножения на 2:

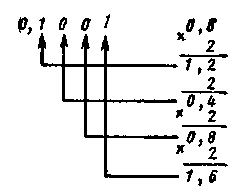
В результате имеем двоичное число 11110, 1001... Если при переводе дробной части получается периодическая дробь, то производится округление, исходя из заданной точности вычисления. В данном примере дробь определена с точностью до пятого знака после запятой.

Аналогично осуществляется перевод чисел из двоичной системы в десятичную. Например, при переводе двоичного числа 111101, 01 в десятичное его целую часть надо делить на основание десятичной системы, которое в двоичной записи будет 1010₂, а дробную умножать последовательно на это число:

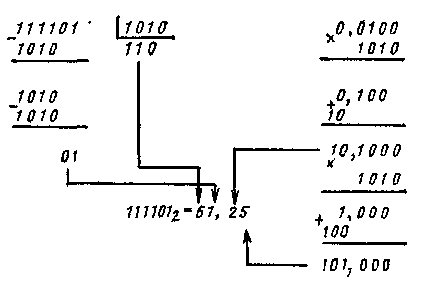
При переводах чисел по рассмотренному алгоритму необходимо выполнять последовательные преобразования, пользуясь таблицями сложения и умножения исходной системы счисления. При переходе вручную к системе с большим основанием такой процесс оказывается неудобным. Поэтому в этом случае применяется другой алгоритм. Сначала для первых чисел находится произведение старшего разряда числа на основание исходной системы счисления, к которому прибавляется следующая цифра переводимого числа. Затем полученная сумма также умножается на основание р, к полученному произведению прибавляется следующая цифра, и т. д. до последнего цикла, в котором осуществляется только прибавление цифры младшего разряда без последующего умножения. При этом действия выполняются в новой системе счисления.

Аналогичная последовательность действий применяется и для перевода дробной части, с той лишь разницей, что для умножения используется величина, обратная основанию и равная р^-1. Например, при переводе двоичного числа 111101,101 в десятичную систему

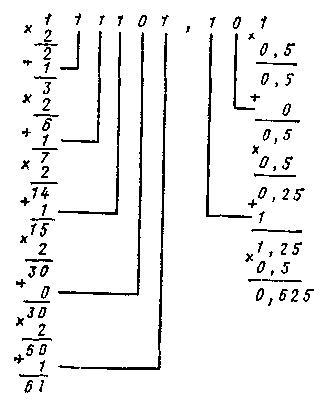
В результате получаем десятичное число 61,625.

Пользуясь стандартным алгоритмом, можно переводить числа из десятичной системы в восьми- и шестнадцатеричные системы и обратно. При этом целая часть числа в десятичной системе последовательно делится на 16 или на 8, а дробная умножается соответственно на 16 или на 8. Например, при преобразовании десятичного числа 39519₁₀ в шестнадцатеричную систему получаем число 9A5F₁₆.

Применение шестнадцатеричной системы счисления позволяет переводить десятичные числа в двоичные и обратно. При этом вначале либо десятичное число переводится в шестнадцатеричное, либо шестнадцатеричное число заменяется двоичным. Например, для перевода числа 509₁₀ в двоичную систему сначала оно должно быть преобразовано в шестнадцатеричную систему

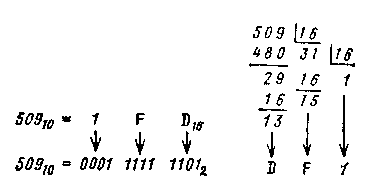
Аналогично осуществляется обратный перевод двоичных чисел в десятичные. Как видно из приведенного примера, при использовании промежуточного перехода к шестнадцатеричной системе счисления существенно сокращается количество операций деления, хотя и появляется дополнительно операция по преобразованию цифр шестнадцатеричной системы в двоичный код.