Задача 1.7. Определить свойства бинарного отношения T, заданного на множестве M2 = {a, b, c, d, e, f} (рис. 1.8).

b f

c d

Рис. 1.8

Решение. Данное бинарное отношение обладает свойствами:

•нерефлексивности (часть вершин имеет петли, часть – нет);

•несимметричности (есть симметричные и антисимметричные

дуги);

•интранзитивности (бинарное отношение обладает несколькими путями длины два, но, ни на один из них нет транзитивного замыкания).

1.3.5. Типы бинарных отношений

Определяя совокупности различных свойств на бинарных отношениях, мы задаем типы бинарных отношений. К ним относятся отношения тождества, эквивалентности, упорядоченности и толерантности.

Отношение тождества. Бинарное отношение U(M), заданное на множестве М, называется отношением тождества тогда и только тогда, когда оно состоит только из пар вида (a,a), a M , т.е.a M (a, a) U (M ) . Обозначается отношение тождества как U.

Отношение эквивалентности. Бинарное отношение T(M), за-

данное на множестве М, называется отношением эквивалентности тогда и только тогда, когда оно рефлексивно, симметрично и транзитивно. Обозначается отношение эквивалентности как <=>.

Классом эквивалентности K(x) элемента x, x M называется множество всех элементов y, y M , с которыми х находится в от-

25

ношении эквивалентности: K(x) = {y/x <=> y}. Отношение эквивалентности разбивает множество М на непересекающиеся классы эквивалентных межу собой элементов, объединение которых совпадает с М.

Задача 1.8. На множестве M = {a, b, c, d, e, f} построить бинарное отношение эквивалентности R при условии, что пара (a,b) R .

Решение. По определению бинарного отношения оно рефлексивно, симметрично и транзитивно. По условию задачи пара (а, b) не принадлежит R. На рис. 1.9 представлены различные бинарные отношения, удовлетворяющие этим условиям.

Задача 1.9. Найти разбиение множество M = {a, b, c, d, e, f} на классы эквивалентности, при условии, что пара (a,b) R .

Решение. По определению класса эквивалентности, это все элементы, между которыми выполняется рефлексивное, симметричное и транзитивное бинарное отношение. На рис.1.9 представлено разбиение М на классы эквивалентности.

Рис. 1.9

Отношение упорядочивания. Бинарное отношение T(M), за-

данное на множестве М, называется отношением упорядоченности тогда и только тогда, когда оно рефлексивно, антисимметрично и транзитивно. Обозначается отношение упорядоченности (порядка) как ≤,≤ (M ) .

Если бинарное отношение T(M) иррефлексивно, антисимметрично и транзитивно, то оно называется отношением строгой упорядоченности <, < (M ) .

26

порядок, в противном случае – частичный порядок.

Рассматривая наиболее часто используемые отношения упорядоченности, можно отметить, что множество чисел упорядочено линейно, а булеан – частично.

Упорядоченные множества принято обозначать с помощью диаграмм Хассе H =< M ,≤>. Диаграмма Хассе представляет собой

графическое представление упорядоченного множества, в котором отсутствуют (но подразумеваются) рефлексивные петли и транзитивные дуги.

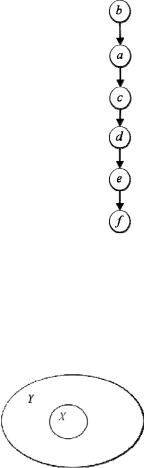
Задача 1.9. Упорядочить множество M = {a, b, c, d, e, f} линейно (т.е. построить ≤ (M ) ), при условии, что пара

(a,b) ≤ .

Решение. По определению линейного порядка, между всеми элементы должны быть в отношении ≤, но пара (a,b) ≤. Для решения этой задачи, в бинарное отношение

нужно включить пару (b,a) ≤. На рис. 1.10 решение за-

дачи представлено диаграммой Хассе.

Теорема 1.2 (Цермело). Всякое непустое множество может быть строго упорядочено [4].

Рис. 1.10

1.3.6. Экстремальные характеристики отношения упорядочивания

Говоря об экстремальных характеристиках частично упорядоченных множеств, следует отметить, что среди исследователей этого вопроса нет полного согласия [1-5]. Рассмотрим подмножество Х

27

Другими словами, из сравнимости элементов xmax X и x X

вытекает, что x ≤ xmax .

Элемент xmin X называется минимальным элементом Х, то-

гда и только тогда, когда среди элементов Х не существует меньших xmin, т.е. ¬( y X ), y ≤ xmin и x ≠ y . Другими словами, из сравнимости элементов xmin X и x X вытекает, что xmin ≤ x .

Теорема 1.3 (принцип максимума). Каждое непустое под-

множество Х упорядоченного множества Y содержит, по меньшей мере, один максимальный (минимальный) элемент.

Элемент xlargest X называется наибольшим элементом, тогда и только тогда, когда для любого x X x ≤ xlargest . Из определения

следует, что наибольший элемент находится в отношении сравнения со всеми элементами их Х.

Элемент xsmallest X называется наименьшим элементом, тогда

28