Lektsii_predely_i_differentsirovanie

Лекция № 1

Функция, ее свойства , способы задания

1.1. Некоторые простейшие логические символы:

– означает «из предложения следует предложение »;

– «предложения равносильны», т.е. из следует , из следует ;

- означает «для любого», «для всякого»;

- «существует», «найдется»;

: - «имеет место»;

1.2. Числовые промежутки, окрестность точки

Напомним, что между точками числовой оси и множествам - действительных чисел, существует взаимнооднозначное соответствие, поэтому вместо слова «число» часто говорят «точка», а подмножества действительных чисел называют числовыми промежутками, или интервалами. Наиболее часто эти множества представляют собой:

1)интервал a;b , т.е. {x a x b}

2)отрезок (сегмент) [a;b] , т.е. {x a x b}

3)полуинтервал, закрытый слева [a;b , {x a x b}

4)полуинтервал, закрытый справа a;b],{x a x b}

Эти множества будем обозначать a;b и называть промежутками.

5) полуось, ;

Любой интервал, содержащий точку x0 , называется окрестностью точки x0 .

Часто рассматривают окрестности, симметричные относительно x0 .

Если из этого интервала выколоть точку x0 , то окрестность называется проколотой - окрестностью точки x0 .

1.3. Функции, способы задания, свойства

Изучая явления, мы обычно имеем дело с совокупностью переменных величин, которые связаны между собой так, что значения одних величин (независимые переменные) полностью определяют значения других (зависимые переменные или функции).

Определение: Переменная величина y называется функцией (однозначной) от переменной x, если они связаны между собой так, что каждому значению величины x из некоторого множества соответствует единственное вполне определенное значение величины y из множества . Записывается этот факт :

Область определения функции f обозначается D(f), множество значений: E(f).

Способы задания функции:

1.Табличный, когда значения аргумента и соответствующие значения функции заданы таблицей.

2.Графический, когда соответствие аргумента и функции даны в виде графика; 3.Аналитический, когда зависимость дана в виде формулы.

1.4. Основные свойства функции:

Определение: Функция у=f(х) называется четной, если для любого

значения х и –х, взятых из области определения функции, выполняется равенство f(-x)=f(x).

Из определения следует, что график четной функции симметричен относительно оси ординат(Оу).

Определение: Функция у=f(х) называется нечетной, если для любого значения х и –х, взятых из области определения функции, выполняется равенство f(-x)= -f(x).

Из определения следует, что график нечетной функции симметричен относительно начала координат.

Примеры нечетных функций: y=, y=sin(x), y=xcos(x), y=tg(x),

Определение: Функция у=f(х) называется периодической, если существует такое число Т>0, что f(x+T)=f(x) для всех х D(f).

Наименьшее число Т, если такое существует, называется периодом функции.

Определение: Функция у=f(x) называется возрастающей на промежутке (а; b), если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует большее значение функции.

Т.е. если для любых (а;b), из условия

.

Определение: Функция у=f(x) называется убывающей на промежутке (а; b), если для любых двух значений аргумента, принадлежащих этому промежутку, большему из них соответствует меньшее значение функции. Т.е. если из .

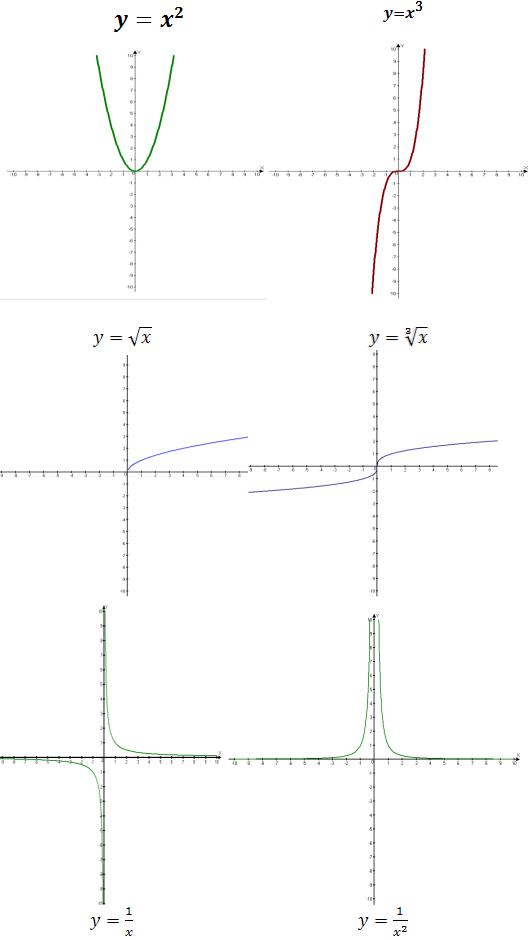
1.5.Основные элементарные функции и их области определения

3. Показательная функция, 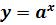, a>0, a≠1, определена на всей

числовой оси. При a>1 функция возрастающая, при а<1 функция убывающая.

4. Логарифмическая функция у= , а>0, а≠1, определена на

интервале (0;∞). При a>1 функция возрастающая, при а<1 функция убывающая.

y=tgx определена на всей числовой оси, исключая точки х= 2 , ;

у=ctgx определена на всей числовой оси, исключая точки х= , .

6. Обратные тригонометрические функции

y=arccosx и y=arcsinx определены на отрезке *-1;1] ;

y=arctgx и y=arcctgx определены на всей числовой оси.

1.6. Сложная функция

Пусть задана функция c множеством определения и множеством значений , и функция y=f(u), областью определения которой является , а множеством значений E(f). Тогда на множестве определена сложная функция (или суперпозиция функций, или функция от функции) с множеством значений E(f). Записывается сложная функция . Переменная называется промежуточным (или внутренним) аргументом функции.

1.7. Обратная функция

Пусть задана функция y=f(x) c областью определения D(f), множеством значений E(f). Если каждому значению соответствует единственное значение , то определена обратная функция (которая иногда обозначается ) с областью определения E и множеством значений D. Про такие функции y=f(x) и говорят, что они взаимно обратные. Для того, чтобы найти функцию , достаточно разрешить уравнение y=f(x) относительно переменной x.

Строго монотонная функция имеет обратную, причем если сама функция возрастает ( убывает), то и обратная так же возрастает( убывает).

Графики функций y=f(x) и изображаются одной и той же кривой. Если же в обратной функции независимую переменную назвать х , а зависимую у, то графики двух взаимно обратных функций y=f(x) и симметричны относительно биссектрисы 1-3 координатных углов.

Пример: Графики двух взаимнообратных функций

-синий и - зеленый.

1.8. Неявная функция

Функция называется явной, если она задана формулой y f x .

Функция называется неявной, если она задана уравнением F x; y 0 , не разрешенным относительно y . Любую явно заданную функцию y=f(x)

можно представить в неявном виде: y-f(x)=0 , однако не всегда неявно заданную функцию можно представить в явном виде.

Примеры:

1.Найти область определения функции:

2.Найти множество значений функции:

5.Даны две функции: составить сложные функции:f(g(x)) и g(f(x)).

6.Найти обратную функцию для данной:

Ответы:

1.(D(f)=(

2.(E(f)=)

3.

4.(

5.(f(g(x))= и g(f(x))=.)

6.(

Лекция № 2

Последовательность. Предел числовой последовательности

2.1. Бесконечная числовая последовательность

Опредедение.1 Бесконечной числовой последовательностью

называется числовая функция, определенная на множестве N натуральных чисел.

Опредедение.2 Последовательность 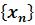называется возрастающей

(убывающей), если каждый ее член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство xn 1 > xn

( xn 1 < xn ).

Опредедение.3 Последовательность называется невозрастающей

(неубывающей), если каждый ее член, начиная со второго, не больше (не меньше) предыдущего, т.е. если для любого п выполняется неравенство xn 1 xn xn 1 xn .

Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.

Опредедение.4 Последовательность называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число т), что для всех членов этой последовательности выполняется неравенство xn М ( xn т). Числа М и т называются соответственно верхней и нижней

границами последовательности . Тот факт, что последовательность ограничена сверху числом М (снизу числом т) геометрически означает, что ни одна точка xn не лежит правее точки М (левее точки т).

Опредедение.5 Последовательность называется ограниченной, если существуют два числа т и М такие, что для всех n выполняется неравенство т xn М. Тот факт, что последовательность ограничена

числами т и М, геометрически означает, что все её члены помещаются в промежутке *т, М+.

Опредедение.6 Последовательность называется постоянной, если все ее члены совпадают.

Обычно последовательность задается формулой, выражающей общий член последовательности через n. Иногда указывается правило, по которому можно вычислить n-й член последовательности по ее известным предыдущим членам, такой способ задания последовательности называется индуктивным (или рекуррентным).