6 Молекулярно-кинетические свойства коллоидных систем.

6.1 Броуновское движение в коллоидных системах. Среднее квадратичное смещение, уравнение Эйнштейна.

Согласно молекулярно-кинетической теории всякий газ представляет собой собрание отдельных молекул, находящихся в хаотическом движении. Среднее расстояние между молекулами газа значительно превосходит средние размеры молекул и они находятся в хаотическом движении. В твердом состоянии молекулы колеблются вокруг узлов кристаллической решетки. В жидком состоянии есть только ближний порядок, но отсутствует дальний порядок. Молекулы совершают как колебательное движение, так и поступательное. В коллоидных растворах и в микрогетерогенных системах с размером частиц 10^-6 м частицы участвуют в тепловом движении. Оно называется броуновским в честь английского ботаника Р. Броуна, обнаружившего его (1827 г.) при наблюдении под микроскопом водной суспензии водной пыльцы. Движение частиц пыльцы не зависело от внешних факторов и ослабевало со временем. Казалось, что оно нарушает второй закон термодинамики. Однако впоследствии пришло понимание того, что броуновское движение является следствием хаотического движения молекул жидкости. Частицы дисперсной системы двигаются в результате огромного числа ударов молекул среды , поэтому они меняют часто положение. За одну секунду коллоидная частица может изменить свое направление свыше 10²³ степени раз. На рис. VI.1 представлена схема броуновского движения коллоидной частицы.

Рисунок VI.1 - Схема броуновского движения частицы дисперсной системы

В связи со сложным движением частиц оно характеризуется среднеквадратичным смещением (), равным среднеквадратичному значению проекций отдельных смещений (∆₁ ², (∆₂ ², ∆₃ ²,…) частицы:

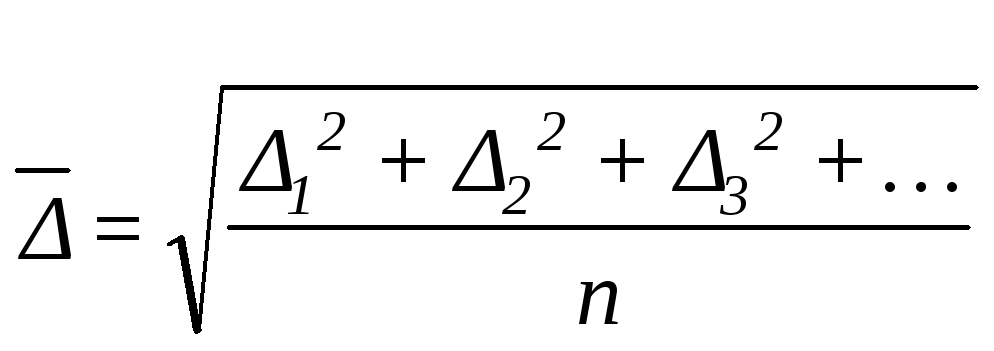. (VI.1)

Как показано далее [см. уравнение (VI.23)], величина среднеквадратичного смещения () не зависит от природы частиц, а зависит прямо пропорционально от температуры и времени и обратно пропорционально от радиуса частиц и вязкости среды.

Осмотическое давление лиозолей, его особенности.

Осмотическое давление для истинных растворов подчиняется закону Вант-Гоффа:

π = сRT, (VI.2)

где с - концентрация растворенного вещества в молях/л.

Закон Вант-Гоффа справедлив и для лиозолей, но для них он записывается через частичную концентрацию ν (число частиц в единиц объема золя):

π = ν kT , ν = сN_А. (VI.3)

Для физических молекул закон Вант-Гоффа записывается также, как и для истинных растворов.

Для коллоидных растворов осмотическое давление имеет малую величину. Грэм считал, что оно полностью отсутствует.

Осмотическое давление коллоидных растворов зависит от размера частиц.

Это легко показать на примере двух растворов с равной массовой концентрацией части (с) сферической формы (с= 4/3 πr³ ν d ):

(VI.4)

Агрегативная неустойчивость приводит к тому, что π ≠ ν kT.

Наблюдает температурный гистерезис: с увеличением температуры наблюдается увеличение, а затем уменьшение давления. Имеет место мембранное равновесие Доннана - сложное равновесие между противоионами в коллоидном растворе во внешнем растворе. Практически осмотическое давление измеряют для ВМС, для определения их молекулярных масс.

Диффузия коллоидных частиц, уравнение Эйнштейна.

Связь коэффициента диффузии с размером частиц дисперсной фазы была установлена Эйнштейном в 1908 году. Для этого Эйнштейн воспользовался уравнением первого закона Фика. В дифференциальной форме закон Фика записывается как:

, (VI.5)

а в интегральной:

, (VI.6)

где m - масса диффундирующего вещества;

D - коэффициент пропорциональности, коэффициент диффузии;

- градиент концентрации в направлении диффузии;

S - площадь сечения, через которое проходит диффузия;

τ - время диффузии.

Рисунок VI.2. Схема, поясняющая вывод уравнения Эйнштейна (принято, что S =1 см², C>C₁ π > π₁, х₁= х + dx, π₁ = π - d π).

Движущая сила диффузии F равна:

. (VI.7)

Проинтегрировав уравнение (VI.1) Вант-Гоффа, получим:

d π = RTdc,

а после постановки значения d π = -Fdx запишем:

-Fdx= RTdc. (VI.8)

Решим это уравнение относительно F:

F= - RT. (VI.9)

Движущая сила должна равняться силе сопротивления:

F=fcN_A, (VI.10)

где в соответствии с законом Стокса сила сопротивления одно сферической частицы

f= Bu = 6πrηu. (VI.11)

Подставив уравнение (VI.11) в уравнение (VI.10), а затем в (VI.9) получим:

- RT = 6πrηucN_A. (VI.12)

При S =1,τ =1 уравнение первого закона Фика запишется:

m = -D. (VI.13)

Проведем преобразование уравнения (VI.12):

uc = m = - RT..(VI.14)

Подставив уравнение (VI.13) в уравнение (VI.14), получим уравнение Эйнштейна для коэффициента диффузии:

D = = (VI.15)

Связь коэффициента диффузии со среднеквадратичным смещением. Уравнение Эйнштейна - Смолуховского.

Разберем схему (рис. VI.3), поясняющую зависимость среднеквадратичного смещения от коэффициента диффузии. На рис.VI.3 представлен разрез трубы, наполненной коллоидным раствором, концентрация которого с₁ и с₂ в отмеченных точках 1 и 2 уменьшается слева на право, т. е. с₁ > с₂. Диффузия также идет слева на право. Расстояние между точками 1 и 2 принято равным среднеквадратичному смещению . Масса дисперсной фазы, перенесенного за время τ вправо и влево через поперечное сечение трубы будут равны:

m₁=1/2 с₁,m₂=1/2 с₂, (VI.16)

а масса m дисперсной фазы диффундирующей слева направо будет равна разности масс m₁ и m₂:

m = m₁ - m₂ = 1/2(с₁ - с₂ ) . (VI.17)

Рисунок VI.3. Схема, поясняющая зависимость от D.

Из рис. VI.3 следует:

,

или

. (VI.18)

Подставляя (с₁ - с₂ ) из уравнения (VI.18) в уравнение (VI.17) получим:

. (VI.19)

Подставляя значение m из уравнения первого закона Фика для диффузии через сечение S = 1 за время τ

m = -D τ. (VI.20)

в уравнение (VI.19) получим

-D= . (VI.20)

Уравнение (VI.20) является уравнением Смолуховского:

D= . (VI.21)

Подставляя значение D из уравнения Эйнштейна в уравнение Смолуховского, получим уравнение Эйнштейна - Смолуховского:

. (VI.22)

Проверка уравнения Эйнштейна - Смолуховского.

Поскольку уравнение Эйнштейна - Смолуховского было выведено для физических молекул, находящихся в хаотическом броуновском движении, подобным движению молекул газа, то доказательство этого уравнения явилось доказательством молекулярно кинетической теории газов. Шведские ученые Сведберг и Зеддиг проводили проверку уравнения, определяя среднеквадратичное смещение, наблюдая под ультрамикроскопом перемещение частиц золя золота. Сведберг доказал справедливость уравнения Эйнштейна - Смолуховского, проверив зависимость и , а Зеддиг -. Перрен определил число Авогадро по уравнению Эйнштейна - Смолуховского:

. (VI.23)

Он проводил опыты с частицами суспензии гуммигута, по размерам относящиеся к физическим молекулам. Полученное им значение близко к значению, определенного другими методами.

Седиментационная устойчивость дисперсных систем.

Частицы дисперсной фазы под влиянием гравитационного поля оседают, или седиментируют. В зависимости от размеров частиц они или выпадут в осадок, или установится их равновесное распределение по высоте. Способность дисперсной системы сохранять равномерное распределение частиц по всему объему называется седиментационной, или кинетической устойчивостью системы. Седиментационная устойчивость имеет место только для свободно дисперсных систем, частицы которых участвуют в тепловом движении. Устойчивость или не устойчивость дисперсной системы определяется соотношением между диффузионным потоком, определяемым тепловым движением и седиментационным, определяемым действием гравитационных сил. Удельный диффузионный поток i_д в соответствии с первым законом Фика равен массе вещества диффундирующего в единицу времени через сечение единичной площади:

i_д = - D. (VI.24)

С учетом уравнения Эйнштейна (VI.15) уравнение (VI.24) запишем:

i_д = - . (VI.25)

Масса оседающих частиц при тех же условиях под действием гравитационного поля (т.е. седиментационный поток i_с) равна произведению скорости оседания на концентрацию, а скорость оседания равна массе одной частицы m на ускорение свободного падения g и деленного на силу сопротивления B, определяемому для сферических частиц законом Стокса (уравнение VI.11). В соответствии с вышесказанным запишем:

i_с = uc = (mg/B)c. (VI.26)

Разделив уравнение (VI.26) на уравнение (VI.25) получим:

(VI.27)

Учет закона Архимеда для частиц объемом v и плотностью дисперсной фазы ρ₁ и дисперсионной среды ρ₂ приводит к уравнению для массы частицы:

m = v (ρ₁ - ρ₂). (VI.28)

Подставив уравнения (VI.28) в уравнение (VI.27), получим:

(VI.29)

При i_д/ i_с>>1имеет место только седиментация, при i_д/ i_с << 1 - только диффузия, при i_д/ i_с = 1 - оба процесса и устанавливается распределение дисперсной фазы по высоте. Преобразование уравнения (VI.29) при и при х =h и его дифференцирование приводит к выражению:

,

а при интегрировании в пределах от с₀ до с_h и от 0 до h получим:

ln с_{0 /} с_h . (VI.30)

Уравнение (VI.30) аналогично гипсометрическому (hypsos - высота) закону Лапласа, где вместо концентрации введена пропорциональная величина - давление газа на разной высоте. Если принять, что концентрации в уравнении (VI.30) - это частичная концентрация ν₁ и ν₂ в суспензии на расстоянии высот Δh при сферической форме частиц, то получим:

ln (ν₁/ ν₂ ). (VI.31)

В случае если принять, что концентрации в уравнении (VI.30) - это частичная концентрация в суспензии на расстоянии высот , на котором концентрация ν₁ уменьшилась в два раза, то получим:

. (VI.32)

Перрен для суспензии гуммигута с размером частиц 0,2 мк установил, что концентрация частиц падает вдвое на высоте 30 мк. Это позволило ему по уравнению (VI.32) рассчитать число Авогадро равным 6,82^.10²³, что близко к принятому в настоящее время.

Различают кинетическую и термодинамическую седиментационную устойчивость. За кинетическую седиментационную устойчивость (КСУ) принимают обратную величину константы седиментации S_сед , определяемую скоростью седиментации

S_сед =. (VI.33)

В соответствии с уравнением (VI.33)

КСУ = . (VI.34)

КСУ определяется гидродинамическими факторами: вязкостью, плотностью и размером частиц; измеряется обратными сведбергами, равными 10¹³с^-1.

Термодинамическая седиментационная устойчивость (ТСУ) определяется статистическим законами диффузии и непосредственно связана с диффузионно - сидиментационным равновесием . Мерой ТСУ является гипсометрическая высота. Ее определяют как высоту h_е, на которой конценрация дисперной фазы изменяется в е раз:

h_е,= . (VI.35)

Уравнение (VI.35) показывает, что гипсометрическая высота и соответственно ТСУ тем больше, чем меньше размер частиц и разность между плотностями частиц и среды. С увеличением температуры термодинамическая устойчивость увеличивается в связи с увеличением теплового движения, а кинетическая уменьшается в связи с уменьшением вязкости.

Седиментационный анализ

Определение размеров частиц дисперсной фазы суспензий и распределение их по фракциям называется дисперсионным анализом. Известно два основных способа седиментационного анализа: в гравитационном и в центробежном поле. Для вывода уравнения, используемого для определения частиц в гравитационном поле, рассмотрим силы, действующие на частицу в гравитационном поле. Оседание происходит под действием гравитационной силы, которая равна произведению массы частицы на ускорение свободного падения и с учетом закона Архимеда для сферических частиц равна:

(VI.36)

Сила F равна силе сопротивления, рассчитываемой по уравнению (VI.11). Приравняв правые части уравнений (VI.36) и (VI.11) получим:

=6πrηu. (VI.37)

Разрешив уравнение (37) относительно радиуса частиц r, получим:

. (VI.38)

Исследование сводится к установлению зависимости скорости оседания во времени. Из этой зависимости по известным из курса физики методикам рассчитывают кривую распределения, показывающую наглядно массу частиц определенного радиуса (фракций).

Для седиментационного анализа в центробежном поле используется уравнение аналогичное (VI.37), в котором скорость оседания равна градиенту продвижения границы оседания частиц dx/dτ, а ускорение свободного падения - угловой скорости на расстояние границы оседания до центра центрифуги ω²x:

ω²x:=6πrη dx/dτ. (VI.39)

После упрощения и разделения уравнения возьмем интегралы с пределами от 0 до τ и от х₁ до х₂:

х₂

∫ω² dτ =6πrη ∫х/dx . (VI.40)

х₁

Значения х₁ и х₂ как расстояния границ оседания в начальный период и во время τ поясняется на рис. VI.4.

Интегрирование уравнения (VI.40) и разрешение его по отношению к размеру частиц позволяет получить уравнение для расчета радиуса частиц:

(VI.41)

Рисунок VI.4. Схема движения границы оседания в центробежном поле.

7 Оптические свойства коллоидных систем.

Учение об оптических свойствах ультра- и микрогетерогенных систем является одним из основных разделов коллоидной химии. С помощью ультрамикроскопических наблюдений коллоидных систем удалось проверить основные молекулярно-кинетические представления, долгое время носившие гипотетический характер. Изучение оптических свойств способствовало количественному истолкованию таких процессов как диффузия, броуновское движение, седиментация и коагуляция. Учение об оптических свойствах коллоидных систем имеет важное практическое значение. В связи с достижениями в этой области созданы оптические методы установления качества продуктов нефтяной и пищевой промышленности.

При падении луча света на коллоидную систему возможны следующие явления:

1. прохождение света через систему;

2. преломление света частицами дисперсной фазы;

3. отражение света частицами дисперсной фазы;

4. рассеяние света (это явление проявляется в виде опалесценции);

5. абсорбция света (поглощение света дисперсной фазой с превращением световой энергии в тепловую).

Прохождение света характерно для неокрашенных систем молекулярной или ионной степени дисперсности (газы, истинные растворы, большинство индивидуальных жидкостей, стекла, кристаллы).

Преломление и отражение света характерно доля микрогетерогенных систем. Если взять крупную частицу, диаметр которой больше половины длины световой волны, происходит преломление (для оптически прозрачных веществ) или отражение света (для оптически не прозрачных веществ) частицами дисперсной фазы по законам геометрической оптики. Такую частичку можно увидеть в обычный микроскоп.