
Вступ до аналізу. Ч. 1
.pdf
. 5 E > 0 N ( E ) (, n > N -
* |
xn |
> E , + *, lim xn = ∞ . |
|
|
n→∞ |
# ! ! *2 " n * xn
+ ! ! *2, + ! * " E . % * + " , -
. |
|
|
|
|
|
|
|||
. 5 |
E > 0 N (E ) |
(, |
n > N - |
||||||
* xn > E , + *, lim xn |
= + ∞ . |
|
|
||||||
|
|
|
|
n→∞ |
|
|
|
||
. 5 |
E > 0 N (E ) |
(, |
n > N - |
||||||
* xn < − E , + *, |
lim xn = − ∞ . |
|
|||||||
|
|
|
|
|
n→∞ |
|
|
|
|
. , lim |
n2 |
= + ∞ . |
|
|
|||||
|
|
|
|
||||||
|
|
|
|
n→∞ n + 1 |
|
|
|
||
6 * E > 0 " *: |
|
||||||||
|
n2 |
1 |
|
|
|
|
|
|
|
|
|
> E n −1 + |
|
> E . |
|
|
|
||
|
|
|
|
|
|
||||
|
n + 1 |
n + 1 |
|
|
|
|
|
||
4' * + ! , " n > E + 1, ! n > N (E ) = [E + 1] .
5 * , ', " * - , * " , + – .
10. & .
" 1 ( ). ) & {xn } ,
.
. .( * {xn } , ( a b ,
a ≠ b . # | a − b | > 0 . ) * lim xn = a , ε > 0 N1 |
n > N1 |
||
|
n →∞ |
|
|
: | xn |
− a | < ε . * lim xn = b , ε > 0 N |
2 n > N |
2 - |
|
n →∞ |
|
|
: | xn − b | < ε . % N = max( N1, N 2 ) . # " n > N ,
! : | xn − a | < ε | xn − b | < ε . % ε = | a − b | 2 . # " n > N :
2 . # " n > N :
| a − b | = | a − xn + xn − b | ≤ | xn − a | + | xn − b | < ε + ε = 2ε = 2 | a − b | . 3
' | a − b | > 0 , , 1 < 2 3 , , , .
3 , , , .
& ( " ! +. ) ( + *
+ " *.
32
" 2 ( ). ) &
, .
. .( * {xn } ! +, lim xn = x0 . # ε > 0
n →∞
N n > N : | xn − x0 | < ε . " n ,:
| xn | = | xn − x0 + x0 | ≤ | xn − x0 | + | x0 | < | x0 | + ε .
% M1 = max | xk | . # n ! : | xn | ≤ M ,
1≤k ≤ N
M= max(M1, | x0 | + ε) . # ! * {xn } ! +.
$ . )! + " , ! ! +
, ! + *. . , * xn = (−1)n ! +, , " . 9 ( 4), , ! + '.
" 3 ( ). -! {xn }, { yn },{zn }
:
1) |
N0 n > N0 : xn ≤ yn ≤ zn ; |
|
|
2) |
lim xn |
= lim zn = a . |
|
|
n →∞ |
n →∞ |
|
. { yn } , lim yn = a . |
|
||
|
|
n →∞ |
|
|
. ) * lim xn = a , ε > 0 N1 n > N1 : | xn − a | < ε . |
||
|
|
n →∞ |
|
! −ε < xn − a < ε . ) * lim zn = a , ε > 0 N |
2 n > N 2 : | zn − a | < ε |
||
|
|
n →∞ |
|
. ! −ε < zn − a < ε . % N = max( N0 , N1, N 2 ) . # " n > N -
:
−ε < xn − a ≤ yn − a ≤ zn − a < ε ,
+ | yn − a | < ε . # " ! * " ε > 0 (2 " N -
(, n > N : | yn |
− a | < ε . ( ,, lim yn = a . #- |
|
n →∞ |
.
4' ' * ! . 5 -
! * ", ! " ' *
", ( (, " ( + , " , + "-. 5 * « » + 2, 2 -
" ' * , ( , + , « » + -
* " , , + . % {xn }, {zn } – « -
», * { yn } – «(».
.
1. ,
lim |
1 |
= 0 . |
|
||
n → ∞ 2n |
|
|
$" " ! .*':
33

2n = (1 + 1)n = 1 + n + n(n −1) + K > 1 + n . 2
6:
0 < |
1 |
< |
1 |
. |
|
|
|
2n |
|
|
|
|
|||
|
|
n + 1 |
|
|
|
||
8 ',, lim |
1 |
= 0 |
. # - |
||||
|
|||||||
|
|||||||
n → ∞ n + 1
, !. 2. , a > 1:
lim n a = 1.
a = 1.
n → ∞
%: αn = n a − 1. # n
a − 1. # n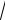 a = 1 + αn , a = (1 + αn )n . 6 - ' ! .*' ,:
a = 1 + αn , a = (1 + αn )n . 6 - ' ! .*' ,:
a = 1 + nαn + ... > 1 + nαn ,
0 < αn < a −1 , n
* lim a −1 = 0 , ,
n →∞ n
!.
3. ,
lim n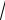 n = 1 .
n = 1 .
n → ∞
%: αn = n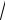 n − 1 > 0 . # n
n − 1 > 0 . # n n = 1 + αn , n = (1 + αn )n . 6 -
n = 1 + αn , n = (1 + αn )n . 6 -
' ! .*' ,:
n = (1 + αn )n = 1 + nαn |
+ |
n(n −1) |
αn2 + ... > |
n(n −1) |
αn2 , |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α2 |
< |
2 |
|
α |
|
< |
|
|
2 |
. |
|
|
|
||
|
|
n |
|
|
|
|
|
||||||||
n |
|
n − 1 |
|
|
|
n |
−1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
#
2
0 < αn < 
 , n − 1
, n − 1
2
* lim = 0 (* (),
n → ∞ n − 1
, !.
" 4. -! lim xn = a , |
lim yn = b , a < b . . N |
n → ∞ |
n → ∞ |
n > N : xn < yn . |
|
34

. ) * |
lim xn = a , ε > 0 N1 n > N1 : | xn − a | < ε . |
|
n → ∞ |
) * lim yn = b , |
ε > 0 N1 n > N 2 : | yn − b | < ε . % |
n → ∞ |
|
N = max( N1, N 2 ) . # " n > N , : | xn − a | < ε , |
|
| yn − b | < ε . !: a − ε < xn < a + ε , b − ε < yn < b + ε . ) * a < b , !- |
|
ε * , ! *: a + ε < b − ε (! ε < (b − a) 2 |
|
). # " n > N ! : |
xn < a + ε < b − ε < yn , ( * - |
|||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# 1. ) & |
|
lim xn = a , |
a < b (a > b) , N n > N - |
|||||||||||||||
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
: |
xn < b ( xn > b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
# 2. 5 |
|
lim xn = a , |
a > 0 ( a < 0 ) , N n > N - |
|||||||||||||||
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
: |
xn > 0 ( xn < 0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
# 3. ) & |
|
lim xn = a , |
|
lim yn = b , |
n xn ≤ yn |
|||||||||||||
|
|
|
n → ∞ |
|
|
|
n → ∞ |
|
|
|
|
|
|
|
||||
, a ≤ b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(, " ! ! a > b , ' 1 ! !, |
xn > yn , ! - |
|||||||||||||||||
' " , * . |
|
|
|
|
|
|
||||||||||||
6, " |
xn ≤ 0 ( xn ≥ 0 ), a ≤ 0 ( a ≥ 0 ) – |
! " - |
||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 + , " ! 3 ! |
xn < yn ( - |
|||||||||||||||||
*), + ! , * " a ≤ b , a < b . 6, " |
xn < 0 ( |
|||||||||||||||||
xn > 0 ), a ≤ 0 (a ≥ 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. .( |
x |
|
= |
|
n |
, y |
|
= |
n + 1 |
|
. ), n x |
|
< y |
|
. |
|||
|
|
|
n |
|
n |
n |
||||||||||||
|
|
n |
|
n |
+ 2 |
|
|
n + 2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
lim xn = lim yn = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n → ∞ |
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. # .
. % * {αn } , * " , "
lim αn = 0 .
n → ∞
# ! " ε > 0 N n > N : | αn | < ε .
., {1 n2}, {1 2n} , ( . . 9,
2 . 10, 1).
". , ! ! -
.
35

. .( {αn }, {βn } – . #
ε > 0 N1 n > N1 : | αn | < ε 2 N 2 n > N 2 : | βn | < ε
2 N 2 n > N 2 : | βn | < ε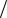 2 . % N = max( N1, N 2 ) . # n > N ! | αn | < ε
2 . % N = max( N1, N 2 ) . # n > N ! | αn | < ε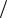 2 ,
2 ,
| βn | < ε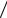 2 . ) +
2 . ) +
| αn |
± βn | ≤ | αn |
| + | βn |
| < |
ε |
+ |
ε |
= ε . |
|
|
||||||
|
|
|
2 |
2 |
|
||
4 ( ,, {αn ± βn } .
* 2 ', * " ! * " -
.
". -
( , ) .
. .( * {xn } – ! +. # M > 0 n : | xn | ≤ M . .( * {αn } . # ε > 0 Nn > N : | αn | < ε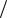 M . # n > N ! :
M . # n > N ! :
| x α |
|
| = | x | | α |
|
| ≤ M |
ε |
= ε . |
n |
n |
|
||||
n |
n |
|
M |
|
||
|
|
|
|
|
|
4 ( ,, * {xnαn } – .
#. ! !
.
(, ( {αn }, {βn } – . % * {βn } , ! + ', * ! +, * {αnβn } – -
.
4" * 2 ', * " ! * " +-
. $ . % ( -
* +. # + !
', + ( !. 0 * + ! ! + '.
.
1. .( αn
αn |
= |
1 n2 |
|
= |
|
n |
||
|
|
n2 |
||||||
βn |
|
|
1 n |
|
||||
|
2. .( αn |
|||||||
αn |
= |
1 n2 |
= |
1 |
|
|||
|
2 n2 |
|
||||||
βn |
|
|
2 |
|
||||
= 1 , βn = 1 . 4 . ? n2 n
=1 + . n
= |
1 |
, β |
|
= |
2 |
. 4 . |
|
n |
|
||||
|
n2 |
|
n2 |
|
||
|
|
|
|
|||
, ', " ', 1 . 2
36
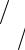
3. .( α |
|
= |
|
1 |
, β |
|
= |
(−1)n |
. 4 . - |
|||||
n |
|
|
|
n |
|
|||||||||
|
|
|
|
|
n2 |
|
n2 |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
αn |
= |
1 n2 |
|
|
= (−1)n , ! + ' ' ( . . 9, - |
||||||||
|
(−1)n |
n2 |
|
|||||||||||
|
βn |
|
|
|
|
|
|
|
|
|||||
4). |
|
|
|
|
|
|
|
|
|
|
|
|
||
". |
lim xn = a ! - |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
xn = a + αn , {αn } – . |
||||||||||||||
. .! *. .( |
lim xn = a . 4 ,, ε > 0 N |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
n > N : | xn − a | < ε . % αn = xn − a . # * {αn } – -
, xn = a + αn .
*. .( xn = a + αn , * {αn } – . # ε > 0 N n > N : | αn | < ε . ) * αn = xn − a , ε > 0 N
n > N : | xn − a | < ε , ! |
lim xn = a . |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
||
. .( x = |
n |
|
. 8 ',, lim x = 1. / ,: |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
n |
n + 1 |
|
|
n → ∞ |
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x = |
|
n |
= |
|
n + 1 −1 |
= 1 − |
1 |
|
= 1 + α |
|
, |
|
||||
|
|
|
|
|
|
|
|
n |
|
|||||||
n |
n |
+ 1 |
|
|
n + 1 |
|
n + 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
αn = − |
1 |
|
|
– . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
n + 1 |
|
|
|
|
|
|
|
|
|||||
" (( ). -! |
||||||||||||||||
lim xn = a, |
lim yn = b . |
. : |
|
|
|
|
||||||||||
n → ∞ |
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|||||
1) lim ( xn ± yn ) = a ± b ;
n → ∞
2) lim ( xn yn ) = ab ;
n → ∞
3) " y |
|
≠ 0, b ≠ 0 , |
lim |
xn |
= |
a |
. |
n |
|
|
|||||
|
|
n → ∞ yn |
|
b |
|||
|
|
|
|
||||
. ) * |
lim xn |
= a, lim yn = b , * |
|||||
|
|
|
n → ∞ |
|
|
n → ∞ |
|
xn = a + αn , yn = b + βn , {αn }, {βn } – -
. 6 xn ± yn = a ± b + αn ± βn . ) * * {αn ± βn } – -
, * ,:
lim ( xn ± yn ) = a ± b . :
n → ∞
xn yn = (a + αn )(b + βn ) = ab + aβn + bαn + αnβn .
) * {αn }, {βn } – ,
{aβn }, {bαn }, {αnβn } + , , ,, ( -
37

* {aβn + bαn + αnβn } – , *
lim ( xn yn ) = ab .
n → ∞
6 , , |
|
lim c = c , , ,, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim (cxn ) = c lim xn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n → ∞ |
|
|
|
n → ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
# ! . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
a |
|
|
|
|
||
, * |
|
n |
− |
|
– . (: |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
b |
|
|
|
|
|||
|
x |
|
|
a |
|
bx − ay |
n |
|
b(a + α |
n |
) − a(b + β |
n |
) |
|
|
a |
1 |
|
||||||
|
|
n |
− |
|
|
= |
n |
= |
|
|
|
|
|
= αn − |
|
βn |
|
. |
||||||
|
|
|
|
|
byn |
|
|
|
byn |
|
|
|
|
|
|
|||||||||
|
yn |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
b |
yn |
|
||||||
) * {αn }, {βn } – , * |
||||||||||||||||||||||||
|
|
|
a |
|
|
|
+ . |
|
|
|
|
|
|
|
|
|
|
|
||||||
αn |
− |
|
βn |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
% +, * {1 yn } ! +. ) * |
lim yn = b ≠ 0 , |
||||||
|
n → ∞ |
|
|
|
|
|
|
ε > 0 N n > N : | yn − b | < ε . # n > N ,: |
|
|
|
|
|
|
|
| yn | = | b + yn − b | ≥ | b | − | yn − b | >|b | −ε . |
|
|
|
|
|
|
|
% ε = | b | 2 . # | yn | > | b | 2 , + n > N : | 1 yn | < 2 |
| b | . |
# ! |
|
||||
* {1 yn } ( ! +. * |
|
|
a |
1 |
|
||
αn − |
|
βn |
|
|
|
||
|
|
||||||
|
|
|
b |
yn |
|
||
– " ! ! +.
x |
|
|
a |
|
x |
n |
|
a |
|||
# * |
|
n |
− |
|
– , + |
lim |
|
= |
|
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
yn |
|
b |
n → ∞ yn |
|
b |
||||||
. % * {xn } , * " , "
lim xn = ∞ .
n → ∞
/ + " + ", " "
" " ! + ' *. . . . -
* ( , ! + '. ! - + " . $" *:
n, & n − , xn = 0, &n − .
4" * ! +, , '. (, " !
! ', E > 0 N n > N : | xn | > E . "
N – , N + 1 – , | xN +1 | = 0 < E . " N – , N + 2 + , | xN + 2 | = 0 < E . ! * " !
, * ".
38

". ) & {xn }, { yn } ,
lim xn = + ∞, lim yn = + ∞ , {xn + yn } |
|
n → ∞ |
n → ∞ |
, |
lim ( xn + yn ) = + ∞ . |
|
n → ∞ |
. ) * lim xn = + ∞ , E > 0 N1 n > N1 : xn > E 2 . |
|
n → ∞ |
|
) * lim yn = + ∞ , E > 0 N |
2 n > N 2 : yn > E 2 . % |
n → ∞ |
|
N = max( N1, N 2 ) yn > E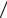 2 . ) +
2 . ) +
. #, " n > N , , * ": xn > E 2 ,
2 ,
n > N : xn + yn |
> E 2 + E 2 = E , ! lim ( xn + yn ) = + ∞ . |
|
n → ∞ |
* ", " lim xn = − ∞ |
lim yn = − ∞ , |
n → ∞ |
n → ∞ |
lim ( xn + yn ) = − ∞ . # ! ( -
n → ∞
, + ' ' + . $ . % * {xn − yn } (+ " -
( ) * -
+ – " * + ! ', + (
!, + * " ( , -
).
.
1. .( xn = 2n2 , yn = n2 . 4 . &
* xn − yn = n2 – + .
2. .( xn = 1 + n, |
|
yn = n . 4 . - |
||||||||||||
* xn − yn |
= 1 , ': lim ( xn − yn ) = 1. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n → ∞ |
3. .( |
x |
= n + |
1 |
, |
y |
|
= n . 4 . - |
|||||||
|
|
n |
||||||||||||
|
n |
|
|
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
* |
x |
− y |
|
= |
1 |
|
, ', * |
|||||||
n |
|
|
||||||||||||
|
n |
|
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. .( x |
= n + (−1)n , |
y |
n |
= n . 4 . |
||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
* x − y |
n |
= (−1)n , " . |
||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
". ) & {xn }, { yn } , -
{xn yn } – .
". ) * * {xn } , E > 0
N1 n > N1 : | xn | > 
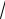 E . ) * * { yn } – ,
E . ) * * { yn } – ,
|
|
|
|
|
|
|
E > 0 N2 n > N2 : | yn | > |
E . %: N = max( N1, N 2 ) . # |
|||||
|
|
|
|
|
|
|
n > N : | xn | > |
|
|
E , | yn | > E . ) + n > N : |
|||
|
39 |
|
|
|||

|
|
|
|
|
|
|
|
| xn |
yn | = | xn |
| | yn |
| > E E = E , ( ,, lim xn yn = ∞ , ! - |
||||
|
|
|
|
|
|
|
n → ∞ |
* {xn yn } – .
$ . % ( -
* +, + " -
. & , * " (.
". , ( , ) -
.
. .( * {xn } – , -
* { yn } – ! +. # M > 0 n : | yn | ≤ M . 0 E > 0 N n > N :
| xn | > E + M . # n > N : | xn + yn | ≥ | xn | − | yn | > E + M − M = E , ! -
* {xn + yn } .
". -
.
. .( xn = C , { yn } – *. #
E > 0 |
N n > N : | yn | > E | C | . ) + n > N : | xn yn | = | Cyn | = |
= | C | | |
yn | > | C | E | C | = E , ! {xn yn } – - |
*. |
|
$ . % ! ! + -
*
+ ( * ().
". ) & n xn ≠ 0 , {xn }
, {1 xn } – .
. .( * {xn } – . # E > 0N n > N : | xn | > E . % +, * {1 xn } – -. " * ! , ε > 0 N1 n > N1 | 1 xn | < ε .
6 * ε > 0 E = 1 ε . " * E ( * " N
(, n > N | xn | > E . # n > N :
1 |
|
= |
1 |
|
< |
1 |
= |
1 |
= ε , |
|
|
|
|
|
|||||
xn |
|
| xn | |
|
E |
1 ε |
||||
( ,, * {1 xn } – .
., ( * {1 xn } – . 4 ,,ε > 0 N n > N | 1 xn | < ε . % +, * {xn } –
. " * ! , E > 0 N1 n > N1 -
: | xn | > E . 6 * E > 0 ε = 1 E . " * ε
( * " N (, n > N | 1 xn | < ε . # n > N -
:
40
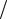
| x | = |
1 |
|
> |
1 |
= E , |
|
|
|
|
||||
n |
1 xn |
|
|
ε |
|
|
|
|
|
|
|||
( ,, * {xn } – . # .
12. % & ! . e . " ' .
". ) & {xn } ,
!,
lim xn = sup{xn}.
n → ∞
. ) * * {xn } ! + , +
X = {x1, x2 ,..., xn ,...} ! + , + , sup X ( . .4). % a =sup X . 6 ' * ε > 0 xN : a − ε < xN ≤ a .
* * {xn } ' ! , n > N ! -
: a − ε < xn ≤ a . 6 " ,,
a = lim xn . # .
n → ∞
* ", " * {xn } ! - ' ! + , ,
lim xn = inf{xn}.
n → ∞
#. ) & , . # ,
. $ . # 2 , * " ' " , !-
+ ( ) ' ! ( ! '-
), * ' " .
.
1. , a :
lim |
an |
= 0 . |
|
|
|
|
|
|
|
|
(12.1) |
||
|
|
|
|
|
|
|
|
|
|||||
n → ∞ n! |
|
|
|
|
|
|
|
|
|
|
|
||
$" a > 0 . # |
|||||||||||||
x |
= |
an |
|
, x |
= |
an+1 |
= |
an a |
= |
a |
x . |
||
|
|
|
|
|
|
|
|||||||
n |
|
n! |
|
n+1 |
|
(n + 1)! |
|
n!(n + 1) |
|
n + 1 |
n |
||
) +, ' " N !:
xn +1 < xn ,
! * {xn } – . n : xn > 0 , ! - 41
