_{Лабораторная работа №1. Дискретное преобразование Фурье}

Цель: Изучение дискретного преобразования Фурье (ДПФ) одномерного дискретного сигнала. Применение теоремы Котельникова для восстановления непрерывного одномерного сигнала по его дискретным отсчетам. Программная реализация ДПФ и ОДПФ для одномерного сигнала.

Программное обеспечение: MS Visual Studio, OpenCV 2.4.0, scilab-5.3.3.

Теория

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и т.д.) преобразуется в последовательность чисел, которая затем подвергается математическим преобразованиям в вычислительном устройстве. Трансформированный цифровой сигнал (последовательность чисел) при необходимости может быть преобразован обратно в напряжение или ток.

Аналоговые, дискретные и цифровые сигналы

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты времени, называют аналоговыми.

Непрерывный гармонический сигнал (рис. 1) описывается выражением:

,

где А – амплитуда, f – частота в Гц, φ – начальная фаза,

ω = 2π • f– угловая частота (рад/с), T = 1/f = 2π/ω-период сигнала.

Рисунок 1 - непрерывный гармонический сигнал и его характеристики

В 1822г. французский инженер и математик Жан Батист Жозеф Фурье (1768-1830) показал, что произвольную периодическую функцию, которая в самом общем виде представляется как s(t)=Acos(ωt+φ), где А-амплитуда, ω-круговая частота и φ-начальная фаза, даже имеющую конечное число разрывов первого рода, можно представить бесконечной дискретной суммой периодических тригонометрических функций в ортонормированном базисе.

Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом и не может полностью соответствовать аналоговому сигналу. Числа, составляющие последовательность, являются значениями сигнала в отдельные (дискретные) моменты времени и называются отсчетами сигнала. Как правило, отсчеты берутся через равные промежутки времени , называемые периодом (или интервалом, шагом) дискретизации. Величина, обратная периоду дискретизации, называется частотой дискретизации: . Соответствующая ей круговая частота определяется следующим образом: . Ясно, что в общем случае представление сигнала набором дискретных отсчетов приводит к потере информации, так как ничего неизвестно о поведении сигнала в промежутках между отсчетами. Однако существует класс аналоговых сигналов, для которых такой потери информации не происходит и которые могут быть точно восстановлены по значениям своих дискретных отсчетов.

Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией, а результат такого преобразования – дискретным сигналом.

При обработке сигнала в вычислительных устройствах его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число отсчетов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню, а возникающие при этом ошибки округления – ошибками (или шумами) квантования.

Сигнал, дискретный во времени, но не квантованный по уровню, называется дискретным сигналом. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым сигналом. Разницу между аналоговыми, дискретными и цифровыми сигналами иллюстрирует рис.2.

Рисунок 2 – Аналоговый (слева), дискретный (в центре) и цифровой (справа) сигналы

Преобразование Фурье. Дискретное преобразование Фурье (ДПФ)

В цифровой обработке сигналов базовой операцией является переход из временной области представления сигнала в частотную область и обратно. Для непрерывного сигнала такой переход осуществляется с использованием прямого (формула 1) и обратного (формула 2) преобразования Фурье.

(1) (2)

где - мнимая единица, ,

- частота,

- время,

- сигнал во временной области,

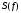- сигнал в частотной области (Фурье спектр).

Для дискретного сигнала преобразование Фурье принимает вид так называемого дискретного преобразования Фурье (ДПФ) (прямое – формула 3, обратное – формула 4):

, ₍₃₎

, ₍₄₎

где - число отсчетов дискретного сигнала .

Для вычисления ДПФ используются формулы Эйлера (формула 5 и 6):

₍₅₎

(6)

Тогда, заменяя комплексную экспоненту выражением Эйлера в формулах (3) и (4), получим:

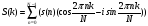(7)

(8)

Векторно-матричная форма дпф и одпф

_{В векторно-матричной форме ДПФ и ОДПФ соответствуют формулы 9 и 10 соответственно:}

(9)

(10)

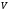где и - матрицы ДПФ для прямого и обратного преобразования соответственно:

а элемент матрицы определяется как ,

- длина вектора дискретных отсчетов сигнала,

- вектор коэффициентов ДПФ.

Как следует из формулы 10 для получения матрицы из матрицы необходимо выполнить комплексное сопряжение элементов матрицы (операция комплексного сопряжения числа заключается в изменении знака у мнимой части этого числа).

Учитывая периодичность степенного ряда элемента матрицы при различных кратностях N выборок на периоде 2π можно записать: , где k mod N есть остаток от деления k на N. Тогда для N=4 матрица примет вид:

Комплексные числа

Сигналы, с которыми приходится иметь дело в ЦОС, обычно имеют значения из области действительных чисел. Однако математические выражения для ряда Фурье в комплексной форме намного проще и на практике постоянно приходится иметь дело с комплексными числами.

Число вида z=a+ib называется комплексным, если в нём a и b любые действительные числа, а - мнимая единица. Комплексное число включает в себя действительную часть a=Re(z) и мнимую часть b=Im(z). На плоскости комплексное число удобно представить на окружности с радиусом z, имеющей декартовы координаты: действительную ось 0x и мнимую ось 0y.

Значение модуля комплексного числа представляется как , а аргумент – это угол между вектором z и осью абсцис: φ=arctg(b/a). Два числа z=a+ib и z=a-ib называются комплексно-сопряженными. Ось абсцисс является действительной, а ось ординат – мнимой осью. Размещение комплексного числа в виде вектора в комплексной форме представлено на рис. 3.

Рисунок 3 - Графическое представление комплексного числа

Как видно из рис.3, комплексное число можно представить кроме алгебраической, также тригонометрической формой следующим образом:

z=a+ib=zcos φ+izsin φ=z(cos φ+isin φ)

На основании тригонометрической формы комплексного числа возможен переход к его показательной форме и формуле Эйлера.

Действия над комплексными числами

Если z₁=a+bi, z₂=c+di, то:

z₁ + z₂ = (a+bi) + (c+di) = (a+c)+(b+d)i;

z₁ - z₂ = (a+bi) - (c+di) = (a-c)+(b-d)i;

z₁*z₂ = (a+bi) *(c+di) = (ac-bd)+(ad+bc)i.

При программировании на С++ для хранения комплексных чисел можно воспользоваться стандартным в C++ STL типом complex (определённым в заголовочном файле <complex>).

_{Пример 1. Расчет ДПФ и ОДПФ}

Найти ДПФ для дискретного сигнала, заданного дискретными отсчетами {2, -1, 1, 4}.

Решение

Подставляя исходные данные в формулу 7, найдем:

.

Аналогично находим:

; ; .

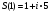Выполним ДПФ и ОДПФ, используя векторно-матричную форму:

Матрица для N=4 имеет вид:

Тогда

Выполним ОДПФ:

Из формул (7) и (8) следует, что для нахождения одного коэффициента или отсчета необходимо выполнить операций умножения на комплексное число и столько же операций сложения. Для определения всех коэффициентов или отсчетов потребуется около вычислений. При такой вычислительной сложности обработка больших массивов данных в реальном времени является трудно решаемой задачей и предъявляет высокие требования к вычислительному устройству по быстродействию и объемам оперативной памяти. Поэтому практически применяют модификации алгоритма вычисления ДПФ.