6. Абстрактные конечные автоматы 1-го и 2-го рода. Матрицы переходов и выходов. Представление графом.

Абстрактный автомат задается как совокупность шести объектов:

• множества входных сигналов Х (входной алфавит автомата);

• множества выходных сигналов Y (выходной алфавит автомата);

• множества состояний автомата А;

• элемента а₀А, называемого начальным состоянием автомата;

• функций переходов (а,x) и выходов (а,x), задающих однозначные отображения множества (а,x), где аА и xX, в множества А и Y.

Абстрактный автомат функционирует в дискретном времени, в каждый момент этого времени имеет определенное состояние а(t) из множества А состояний автомата. В каждый момент времени, отличный от начального, автомат способен воспринимать входной сигнал x(t) – произвольную букву входного алфавита X и выдавать соответствующий выходной сигнал y(t) – определенную букву выходного алфавита.

Закон функционирования автомата первого рода задается уравнениями вида:

а(t)= [а(t-1), x(t)]; y(t)=[а(t-1), x(t)]; t=1,2,...;

(7)

Закон функционирования автомата второго рода:

а(t)= [а(t-1), x(t)]; y(t)=[а(t), x(t)]; t=1,2,...

(8)

В практике используют:

• автомат Мили: произвольный конечный автомат первого рода;

• автомат Мура: частный случай конечных автоматов второго рода, у которого функция выходов (а,x) не зависит от переменной х.

Автомат называется конечным если конечно число его состояний. Автоматы задают табличным способом или направленным графом. В первом случае строят матрицы переходов и выходов. Строки обеих этих таблиц обозначаются входными сигналами автомата, а столбцы – его состояниями. На пересечении строки и столбца таблицы переходов ставится соответствующее значение функции переходов (а,x), а в таблице выходов – значение (а,x).Для автомата Мура сдвинутая таблица выходов сводится к одной строке, поэтому часто в таблице переходов над каждым состоянием а_i автомата, обозначающим тот или иной столбец таблицы, ставят соответствующий этому состоянию выходной сигнал  (а_i,x)= (а_i).

При задании автомата с использованием направленного графа вершины графа отождествляются с состояниями автомата, а стрелки – с выходными сигналами. Если входной сигнал x_i вызывает переход автомата из состояния а_j в состояние а_k, то на графе автомата этому сигналу соответствует помеченная буквой x_i стрелка, соединяющая вершину, соответствующую состоянию а_j, с вершиной, соответствующей состоянию а_k. Для задания функции выхода ребра графа также помечаются соответствующими выходными сигналами. Если обозначенная входным сигналом x_i стрелка соединяет вершину а_j с а_k, то в случае автоматов первого рода ей предписывается выходной сигнал (а_j,x_i), а в случае автоматов второго рода – выходной сигнал (а_k,x_i) (см. рис. 12).

Пример графа АКА первого рода представлен на рис. 13, а соответствующие ему матрицы переходов и выходов – в таблицах 5 и 6.

Таблица 5

Таблица 6

Матрица переходов

Матрица выходов

А

B

C

D

E

А

B

C

D

E

x1

B

C

D

E

A

x1

y1

y2

y3

y4

y5

x2

E

C

D

D

E

x2

y2

y3

y2

y4

y5

x3

A

B

D

B

A

x3

y5

y1

y2

y5

y1

Пример графа АКА второго рода представлен на рис. 14, а соответствующие ему матрицы переходов и выходов – в таблицах 7 и 8.

Таблица 7

Таблица 8

Матрица переходов

Матрица выходов

a

b

c

d

e

a

b

c

d

e

х1

b

c

e

a

d

х1

y5

y1

y2

y3

y3

х2

c

d

b

e

a

х2

y5

y4

y1

y2

y4

В случае автомата Мура все стрелки, входящие в одну и туже вершину а_k, должны быть обозначены одним и тем же выходным сигналом. Поэтому принято обозначать выходными сигналами не стрелки, а вершины, в которые эти ребра входят, т. е. на графе автомата Мура каждая вершина имеет два обозначения – одно, определяющее состояние автомата, и другое, обозначающее выходной сигнал.

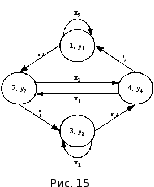
Пример графа АКА Мура представлен на рис. 15, а соответствующая ему совмещенная матрица переходов и выходов – в таблице 9.

Таблица 9
Совмещенная матрица переходов и выходов
y	y1	y2	y3	y4
а	1	2	3	4
x1	2	3	3	2
x2	1	4	4	1

ПРИМЕРЫ автоматных моделей дискретных устройств.

Для моделирования элементов вычислительных систем и сетей, проявляющих статистически закономерное случайное поведение, можно использовать вероятностные автоматы. Вероятностный автомат определяется, в дополнение с семейству множеств X, Y, А конечного автомата, семейством матриц {M(y/x)}. Если Х(x₁...x_l) – входной алфавит, Y(y₁...y_m) – выходной алфавит, A(a₁...a_n) – множество состояний, то M(y/x) – семейство lm матриц размерностью nn. Элемент _ij(y_p/x_r) матрицы М(y_p/x_r) есть вероятность _ij(y_p/x_r)=Р(y_p, a_j/a_i, x_r), i, j=1...n, того, что, находясь в состоянии a_i и получив входной сигнал xi, автомат перейдет в состояние a_j, а выходной сигнал будет y_p. Если _ij(y_p/x_r) принимает только значения единицы или нуля, имеем частный случай вероятностного автомата – обычный детерминистический конечный автомат [3, 6, 20].