
- •Введение
- •1.3. Погрешность функционирования средств измерений
- •2.4. Фазочувствительные детекторы и усилители
- •3. Методы оценки точности средств измерений
- •3.1 Метрологический анализ
- •3.2. Метрологический синтез
- •3.3. Оптимизация динамических характеристик СИ
- •4. Повышение точности и помехоустойчивости СИ
- •4.1. Методы повышения точности СИ
- •4.2. Методы повышения помехоустойчивости СИ.
- •4.3. Статистические методы оценки надежности СИ
- •Приложения
- •1. Характеристики случайных процессов
- •2. Корреляционные функции и спектральные плотности
- •3. Определение переходной функции системы
- •5. Примеры решения задач
- •Литература
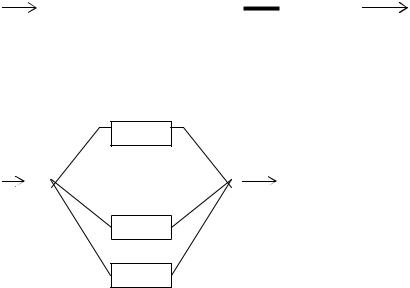
3.Методы оценки точности средств измерений
3.1Метрологический анализ
Под метрологическим анализом понимается анализ точности измерений или, в более узкой постановке, точности функционирования СИ. Для его проведения необходимо построить модель СИ, в частности, его структурной схемы. Многообразие структурных схем СИ может быть сведено к конечному набору типовых моделей, характеризуемых двумя факторами: типом схемы и числом входов-выходов. Выделим следующие типовые модели:
1) линейная с одним входом и одним выходом:
а) последовательное соединение элементов (рис.13а); б) параллельное соединение элементов (рис.13б);
2)линейная с одним входом и многими выходами (рис.13в);
3)линейная с многими входами и одним выходом (рис.13г);
4)циклическая с одним входом и одним выходом (рис13д);
|
|
|
f1 |
|
f2 |
|
|
|
fk |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|||
x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
элементов: х – входной сигнал, |
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
Рис.13а. Линейная схема с последовательным соединением |
||||||||||||
y – выходной сигнал; f1,…,fk – функции преобразования отдельных элементов (СИ).
f1
х |
f2 |
y |
||
|
|
|
|
|
|
|
|
|
|
fk
Рис.13б. Линейная схема с параллельным соединением элементов.
Ошибка!
|
|
|
|
|
|
|
f (1) |
||
|
|
|
|
|
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (2) |
||
|
|||||||||
x |
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (k)
yk
Рис. 13в. Линейная схема с одним входом и многими выходами.
f (1)
xl
f (2)
x2
y
xk f (k)
Рис.13г. Линейная схема с многими входами и одним выходом.
|
|
f1 |
|
x |
|
|
y |
|
|
||
|
|
|
|
f2
Рис.13д. Циклическая схема с одним входом и одним выходом.
Для схемы на рис. 13,а при произвольных функциях преобразования погрешность в квадратичном приближении определяется системой рекуррентных соотношений
y = |
∂y |
f |
|
+ |
∂y |
y |
+ |
1 |
∂2 y |
f |
|
2 |
+ |
1 |
∂2 y |
|
y |
|
2 |
+ |
|
|
i |
|
i |
|
i ( |
) |
|
|
i |
( |
) |
|
|||||||||
∂f |
|
∂y |
2 |
|
2 |
|
|||||||||||||||
i |
i |
|
i |
|
i−1 |
|
∂f 2 |
i |
|
|
|
∂y2 |
|
i−1 |
|
|
|
||||
|
|
|
|
|
i−1 |
|
|
|
i |
|
|
|
|
|
i−1 |
|
|
|
|
|
|
|
∂2 y |
|
|
|
|
|
+ |
i |
( f |
i |
y |
), i =1,..., k . |
(3.1.1) |
|
||||||
|
∂fi∂yi−1 |
i−1 |
|
|
||
|
|
|
|
|
||
Вводя чувствительности Si=∂yi/∂yi-1, выражение (3.1.1) можно записать в виде
y = |
∂y |
f |
|
+ S |
y |
+ |
1 |
∂2 y |
f |
|
2 |
+ |
1 |
∂S |
i |
|
y |
|
2 |
+ |
|
|
i |
|
|
i ( |
) |
|
|
|
( |
) |
|
||||||||||
∂f |
|
2 |
|
2 |
∂y |
|
|
||||||||||||||
i |
i |
|
i |
|
i i−1 |
|
∂f 2 |
i |
|
|
|
|
|
i−1 |
|
|
|
||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
i−1 |
|
|
|
|
|
||
+ |
∂Si ( f |
i |
y |
) , |
(3.1.1а) |
|
∂fi |
i−1 |
|
|
|
|
|
|
|
|
где yi=fi(yi-1); y=fk(fk-1… f1(x)); y0=x.
В частности, при i=1 (схема из одного элемента) имеем
|
y = |
∂y |
f + |
∂y |
x + |
1 ∂2 y |
( f ) |
2 |
+ |
1 ∂2 y |
( x) |
2 |
+ |
|||
|
|
1 |
1 |
2 |
1 |
|
1 |
|
||||||||
|
1 |
∂f |
1 |
∂x |
|
∂f 2 |
1 |
|
|
2 ∂x2 |
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
+ |
|
∂2 y |
( |
f x) , |
|
|
|
|
|
|
|
|
|
(3.1.1б) |
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂f1∂x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где y1=y=f1(x);
Вводя чувствительность S1=∂y1/∂x, получим из (3.1.1б)
y ≡ |
y = |
∂y |
f + S x + |
1 ∂2 y |
( f ) |
2 |
+ |
1 ∂S |
( x) |
2 |
+ |
1 |
1 |
|
1 |
|
|||||||
1 |
|
∂f |
1 1 |
2 ∂f 2 |
1 |
|
|
2 ∂x |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
+ |
∂S1 ( f x) . |
(3.1.1в) |
|
1 |
|
|
∂f1 |
|
В выражениях (3.1.1, 3.1.1в) два первых слагаемых соответствуют линейному приближению. Для проведения расчетов нужно знать вид функций преобразования. Рассмотрим случай, наиболее важный для практики и, одновременно,
наглядный, когда функции преобразования элементов fi являются постоянными. При учете только погрешности входного сигнала имеем
1 |
|
y = ∏ Si х = S x , |
(3.1.2) |
i=k
где ∆y – погрешность сигнала на выходе; ∆х – погрешность сигнала на входе, S – чувствительность схемы.
Относительная ошибка определения погрешности выходного сигнала из (3.1.2) определяется выражением
|
( y) |
k |
(3.1.3) |
δ y ≡ |
= ∑δ Si + δ x , |
||
|
y |
i=1 |
|
где δSi – относительная ошибка определения чувствительности i-го элемента схемы, δ x – относительная ошибка входного сигнала. Отметим, что погрешность считается значимой, если
δ y < 0.5 .
Выражение (3.1.2) не учитывает отклонение реальной функции преобразования от идеальной (номинальной). При учете этого фактора погрешность выходной величины находится из соотношения:
k |
|
∂y |
|
∂y |
|
|
y = ∑ |
|
fi + |
x , |
(3.1.4) |
||
|
∂fi |
∂x |
||||
i=1 |
|
|
|
|
||
где fi |
– отклонение реальной функции от идеальной для i-го |
|||||
элемента схемы.
Второе слагаемое в (3.1.4) определяется погрешностью входного сигнала и совпадает с (3.1.2). Первое слагаемое учитывает вклад элементов схемы из-за отличия реальной функции преобразования от идеальной и записывается в виде
k |
∂y |
k |
1 |
|
|
∑ |
fi = ∑ fi ∏ f j х, |
(3.1.4а) |
|||
∂fi |
|||||
i=1 |
i=1 |
j=k |
|
||
|
|
|
j≠i |
|
|
Если учитывать не только линейные, но и квадратичные члены по ∆х, то выражение для погрешности входной величины принимает вид
k |
1 |
1 |
k |
k |
1 |
y(2) = y(1) + ∑ fi ∏ f j х+ |
∑ fi ∑ f j ∏ fl х+ |
||||
i=1 |
j=k |
2 i=1 |
j=1 |
l=k |
|
|
j≠i |
|
|
j≠i |
l≠i, j |
k |
1 |
(3.1.5) |
+ ∑ fi |
x∏ f j , |
|
i=1 |
j=k |
|
|
j≠i |
|
где fi – абсолютная погрешность функции преобразования, ∆y(1)
определяется соотношением (3.1.2) и учтено, что в данном
случае Si= fi.
Определим математическое ожидание и дисперсию погрешности. В линейном приближении при учете только погрешности входного сигнала для математического ожидания и дисперсии имеем соответственно из (3.1.2)
M [ |
k |
x], |
(3.1.6) |
y]= ∏Si M [ |
|||
|
i=1 |
|
|
D[ |
k |
x], |
(3.1.7) |
y]= ∏Si2 D[ |
i=1
Вболее общем случае из соотношения (3.1.4) найдем
M [ |
|
k |
|
fi ] |
1 |
|
|
1 |
|
|
|
x], |
|
|
|
|
|
|
|
|
|
|
(3.1.6а) |
|
y]= ∑M [ |
∏ f j x + |
∏Si M [ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
i=1 |
|
|
|
j=k |
|
|
i=k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D[ |
|
k |
|
|
|
1 |
|
2 |
|
1 |
2 |
x], |
|
|
|
|
|
|
|
|
(3.1.7а) |
|||
y]= ∑D[ |
fi ] |
∏ f j x |
+ |
∏Si |
|
D[ |
|
|
|
|
|
|
|
|
||||||||||
|
|
i=1 |
|
|
|
j=k |
|
|
|
i=k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В квадратичном приближении из (3.1.5) найдем |
|
|
|
|
|
|||||||||||||||||||
M [ |
y]= |
k M [ |
f |
] |
1 |
f |
x + |
1 |
S |
M [ |
|
x]+ |
1 k |
k |
M[ |
f |
i |
f ] 1 |
f |
х+ |
|
|
||
|
|
∑ |
|
i |
|
∏ j |
|
∏ i |
|
|
|
∑∑ |
|
|
j ∏ l |
|
|
|
|
|||||
|
|
i=1 |
|
|
|
j=k |
|
|
i=k |
|
|
|
|
2 i=1 j=1 |
|
|
|
l=k |
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
j≠i |
|
|
|
l≠i, j |
|
|
|
|
|
k |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.6б) |
|
∑M[ fi |
x]∏ f j , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
i=1 |
|
j=k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
1 |
|
2 |
|
1 |
|
2 |
|
1 |
k |
k |
|
|
|
|
1 |
2 |
||
D[ |
|
|
|
|
|
|
D[ |
x]+ |
|
|
|
|
|
|
||||||||||
y]= ∑D[ |
fi ] |
∏ f j x |
+ |
∏Si |
|
∑∑D[ fi |
f j ] |
∏ fl х |
+ |
|||||||||||||||
|
|
i=1 |
|
|
|
j=k |
|
|
|
i=k |
|
|
|
4 i=1 j=1 |
|
|
|
l=k |
|
|
||||
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
l≠i, j |
|
|
|
k |
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.7б) |
||
∑D[ fi |
∏ f j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i=1 |
|
|
j=k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если погрешности fi , ∆х – случайные центрированные, то |
|||||||||||||||||||||||
M [ |
fi ]= 0 |
и |
|
M [ |
x]= 0 , |
т.е. |
|
и |
M [ |
y]= 0 . |
|
Если |
|
fi |
и |
∆х – |
||||||||
систематические, то их математические ожидания отличны от нуля, и, следовательно, M [ y]≠ 0 . Аналогично рассчитываются математическое ожидание и дисперсия погрешности в более
сложных случаях, однако результаты получаются менее наглядными. Для многих СИ наряду с абсолютной погрешностью
целесообразно задавать относительную погрешность δ y = yy . Для
рассматриваемой схемы связь между входом и выходом представима в виде (см.§ 1.3)
y = f k f k −1 ..... f 1 x . |
(3.1.8) |
Отсюда, используя соотношение (3.1.4), после преобразований получим в линейном приближении
k |
|
δ y = ∑δ fi +δ x , |
(3.1.9) |
i=1 |
погрешность функции преобразования i- |
где δfi - относительная |
го элемента схемы; δх - относительная погрешность входного сигнала.
В квадратичном приближении после ряда преобразований имеем
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
δ y(2) |
=δ y(1) |
+ 1 ∑δ fi ∑δ f j |
+ ∑δ fiδ х, |
|
(3.1.10) |
|||||||
|
|
2 i=1 |
|
j=1 |
|
i=1 |
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
где δ y(1) определяется выражением (3.1.9). |
|
|
||||||||||
|
Если функции преобразования являются номинальными, то |
|||||||||||
δfi = 0 |
и |
относительная |
|
погрешность |
выходного |
сигнала |
||||||
определяется погрешностью входного сигнала. |
|
|
||||||||||
|
Определим математическое ожидание и дисперсию |
|||||||||||
относительной погрешности. Считая погрешности |
δfi |
|||||||||||
некоррелированными, из (3.1.10) получим |
|
|
|
|||||||||
|
|
|
k |
|
|
1 k |
|
k |
|
|
|
|
M [δ y]= M [δ x]+ ∑M [δ fi ]+ |
|
∑∑M |
δ fiδ f j |
+ |
|
|
||||||
|
|
|
i=1 |
|
|
2 i=1 |
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
(3.1.11) |
|
∑M [δ fiδ x], |
|
|
|
|
|
|
|
|
|
|||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
k k |
|
|
|
1 |
|
(3.1.12) |
||
D[δ y]= D[δ x]+ ∑D[δ fi ]+ 1 ∑∑D δ fiδ f j +∑D[δ fiδ x] |
||||||||||||
|
|
i=1 |
|
4 i=1 j |
=1 |
|
|
i=k |
|
|
|
|
|
|
|
|
j |
≠i |
|
|
|
|
|
|
|
При практических расчетах можно принять, что |
||||||||||||
погрешности δfi и δx |
независимы, |
поэтому M [δfiδx]= M [δfi ]M [δx]; |
||||||||||
D[δ fiδ x]= D[δ fi ]M (δ x) |
+ D[δ x]M |
|
[δ fi ]. Аналогичное утверждение |
|||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
справедливо также для δfi и δ f j .
Если положить |
δfi = const(i) , т.е. погрешности |
для |
всех |
|||||
элементов схемы одинаковы, и погрешность δx |
пренебрежимо |
|||||||
мала, то из (3.1.11) получаем |
|
|
|
|||||
M [δy]= kM [δfi ]+ |
1 |
k(k −1)M [(δfi )2 ] |
|
(3.1.11а) |
||||
|
|
|
||||||
2 |
|
|
|
|
|
|||
Соотношение |
(3.1.12) для дисперсии |
при |
тех |
же |
||||
предположениях принимает вид |
|
|
|
|||||
D[δy] = kD[δfi ]+ |
1 |
k(k −1)D[(δfi )2 ] |
|
(3.1.12а) |
||||
|
|
|||||||
4 |
|
|
|
|
|
|
||
Таким образом, математическое ожидание и дисперсия относительной погрешности выходного сигнала возрастает в k раз по сравнению с соответствующими величинами для отдельного элемента схемы (без учета квадратичных слагаемых). Для схемы на рис.13,б в квадратичном приближении получается следующее общее соотношение
|
|
|
k |
|
2 |
y2i ( |
k |
|
2 |
yi |
|
k |
|
2 |
y2i ( |
|
|
y(2) = |
y(1) + |
1 |
∑∂ |
x)2 + 2∑ |
∂ |
( |
x fi ) + ∑∂ |
fi )2 , |
|||||||||
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
||||||||||||
|
|
i=1 |
∂x |
i=1 |
∂x∂fi |
i=1 |
∂fi |
|
|||||||||
где y(1) – выражение для погрешности в линейном приближении; yi=fi(x); y=y1+…+ yk. Для y(1) имеем
k |
k |
∂y |
y(1) = ∑Si |
x + ∑ |
i fi , |
i=1 |
i=1 |
∂fi |
Рассмотрим случай, когда функции преобразования являются постоянными. В тех же обозначениях при учете только погрешности входного сигнала имеем
k |
|
y = ∑S i x , |
(3.1.13) |
i=1 |
|
причем Si= fi. |
|
Для относительной ошибки погрешности найдем |
|
δ y =δS +δ x , |
(3.1.14) |
k
где S = ∑Si - чувствительность схемы.
i=1
Если учесть отклонение реальной функции преобразования от идеальной, то выражение для абсолютной погрешности принимает вид
k |
k |
|
y(1) = ∑ fi x + ∑Si x , |
(3.1.13а) |
|
i=1 |
i=1 |
|
В квадратичном приближении для погрешности получим
|
|
k |
|
|
|
|
|
|
(3.1.13б) |
y(2) = |
y(1) +∑ fi x , |
|
|
|
|
|
|||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
Определим математическое ожидание и дисперсию |
|||||||
абсолютной погрешности из (3.1.13б) |
|
||||||||
M [ |
|
k |
|
k |
|
[ |
k |
x], |
(3.1.15) |
y]= ∑M [ |
fi ]x +∑Si M |
x]+∑M [ fi |
|||||||
|
|
i=1 |
i=1 |
|
|
i=1 |
|
|
|
D[ |
y] |
k |
fi ]x2 + |
k |
|
2 |
k |
fi x]. |
(3.1.16) |
|
|
||||||||
= ∑D[ |
∑Si |
|
D[ x]+ ∑D[ |
||||||
|
|
i=1 |
|
i=1 |
|
|
i=1 |
|
|
Определим относительную погрешность. Для параллельной схемы связь между входом и выходом представима в виде
(см.§1.3.)
|
k |
|
(3.1.17) |
y = ∑ fi x , |
|
||
i=1 |
|
|
|
|
С учетом (3.1.13а) после ряда преобразований получим |
||
|
k |
k |
(3.1.18) |
δ y(1) |
= ∑ fiδ fi / |
∑ fi +δ x , |
|
|
i=1 |
i=1 |
|
|
В квадратичном приближении вместо (3.1.18) имеем |
||
|
k |
k |
(3.1.18а) |
δ y(2) |
=δ y(1) +∑ fiδ fiδ x / ∑ fi , |
||
|
i=1 |
i=1 |
|
где δy(1) - определяется выражением (3.1.18).
Для математического ожидания и дисперсии относительной погрешности имеем соответственно
|
|
k |
[δ fi ] |
k |
|
|
|
M [δ y]= ∑ fi M |
/ ∑ fi + M[δ x] + |
||||||
|
|
i=1 |
|
|
i=1 |
|
|
k |
|
|
k |
|
|
|
|
+∑ fi M [δ fiδ x] |
/ ∑ fi , |
|
(3.1.19) |
||||
i=1 |
|
|
i=1 |
|
|
|
|
D[δ y]= ∑ fi 2 D[δ fi ]/ ∑ fi |
|
2 |
|||||
+ D[δ x]+ |
|||||||
|
|
k |
|
k |
|
|
|
|
|
i=1 |
|
i=1 |
|
|
|
k |
2 |
k |
|
2 |
|
|
(3.1.20) |
+∑ fi |
D[δ fiδ x]/ ∑ fi |
|
|
|
|||
i=1 |
|
i=1 |
|
|
|
|
|
Если принять, что δ fi = const (i) |
, то (3.1.19), (3.1.20) |
упрощаются |
|
M [δ y]= M [δ fi ]+ M [δ x]+ M [δ fiδ x], |
(3.1.19а) |
k |
k |
2 |
|
D[δ y]= D[δ fi ]∑ fi 2 |
/ ∑ fi |
+ D[δ x]+ |
|
i=1 |
i=1 |
|
|
k |
2 |
|
k |
2 |
(3.1.20а) |
+D[δ fiδ x]∑ fi |
|
/ |
∑ fi |
||
i=1 |
|
|
i=1 |
|
|
Если положить fi = const (i) и δx=0, то имеем: |
|
||||
M[δ y] = M[δ fi ] , |
|
|
(3.1.19б) |
||
D[δ y] =1/ kD[δ fi ] . |
|
|
(3.1.20б) |
||
Из полученных соотношений следует, что математическое ожидание погрешности не изменяется, а составляющая дисперсии, зависящая от погрешности преобразования уменьшается в k раз по сравнению с дисперсией относительной погрешности для отдельного элемента схемы.
Схема на рис.13,в сводится к нескольким схемам, представленным на рис.13,а, так что получаем систему уравнений для определения погрешности выходной величины. При этом функции f(1),…,f(k) могут содержать несколько составляющих, что не принципиально. Для погрешностей выходных величин каждой ветви справедливы соотношения (3.1.1) – (3.1.7). Например, выражение (3.1.2) запишется в виде:
k j |
x , |
(3.1.21) |
||
y( j) = ∏Si(j ) |
||||
i=1 |
|
|
|
|
где j -номер |
ветви, |
j = |
|
; k j - число элементов в j − ой ветви |
1,l |
||||
схемы.
Схема на рис.13,г сводится к схеме на рис.13,б с учетом того, что сигналы на входе каждой ветви различны. При этом, как и в предыдущем случае, каждая ветвь может состоять из последовательных или параллельных элементов. Считая, что
операторы |
f в каждой ветви простые |
из (3.1.13а) |
|
l |
l |
y(1) = ∑S (j ) |
x(j ) + ∑x(j ) f (j ), |
j=1 |
j=1 |
(не составные), получим
(3.1.22)
где l − число ветвей.
В квадратичном приближении имеем соотношение, аналогичное (3.1.13б)
l |
(3.1.22а) |
y(2) = y(1) +∑ f ( j) x( j) , |
j=1
где y(1) - определяется из соотношения (3.1.22)
Аналогично могут быть записаны и другие соотношения для данной схемы.

Для схемы на рис.13,д в линейном приближении можно записать
|
(1) |
|
∂f |
|
∂y |
|
∂z |
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y |
|
= |
1 |
x + |
1 f1 |
+ |
|
f1 |
signf2 |
+ |
|
|
f2 |
signf2 |
|
/ Q , |
|
|
|
|
|||||||||||||
|
|
|
∂x |
|
∂f1 |
|
∂f1 |
|
|
|
∂f |
2 |
|
|
|
|
где Q=(1–∂z/∂y signf2); y1=f1(x); z=f1(f2(y)); y–f1(f2(y)) signf2=f1(x);
∂z/∂y=(∂f1/∂f2)(∂f2/∂y). В квадратичном приближении получаем для погрешности при произвольных функциях преобразования
|
|
y |
(2) |
= |
|
|
|
|
y |
(1) |
+ |
|
{ |
1 |
|
∂ |
2 f |
|
|
|
|
|
|
|
|
|
|
|
x) |
2 |
+ |
|
1 |
( |
∂2 y |
+ |
∂2 z |
|
|
signf |
|
|
|
)( f ) |
2 |
+ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
∂f |
2 |
|
|
|
|
∂f |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
+ |
1 ∂2 z |
|
signf |
|
|
|
( |
|
f |
|
) |
2 |
|
+ |
|
|
∂2 y |
|
|
( |
|
|
|
f |
|
|
x)}/ Q + |
|
1 ∂2 z |
|
signf |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
∂f 2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
∂f ∂x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
∂y2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
{(∂f1 )2 ( |
|
|
x)2 +(∂y1 + |
|
|
|
∂z |
|
|
signf |
2 |
|
|
)2 |
( |
|
f )2 +( |
∂z |
)2 ( |
|
|
|
f |
2 |
)2 |
|
+ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f1 |
|
|
|
|
|
∂f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 ∂f1 (∂y1 + |
∂z |
|
|
|
signf |
2 |
|
|
)( |
|
|
|
|
x |
|
f ) |
+ 2 ∂f1 |
∂z |
|
|
|
|
|
|
signf |
2 |
|
( |
|
|
|
x |
|
f |
2 |
) |
|
+ |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
∂x ∂f1 |
|
|
|
|
|
∂f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
∂x |
∂f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
∂y1 |
|
∂z |
|
|
signf |
2 |
|
( |
|
|
f |
|
|
f |
2 |
|
|
)}/ Q3 +{(∂y1 + |
|
∂z |
|
|
|
|
|
|
signf |
2 |
|
|
)( |
|
|
|
f |
|
)2 |
|
+ |
|
|
∂f1 ( |
f |
x) + |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂f1 ∂f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f1 |
|
∂f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
∂x |
1 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ∂2 z |
|
|
|
|
|
|
|
|
|
|
|
|
1 ∂2 z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂z |
|
|
|
signf |
2 |
|
( |
|
f |
|
|
|
|
f |
2 |
)} |
|
|
|
|
|
signf |
2 |
|
/ Q |
2 |
|
+ |
|
|
|
|
signf |
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 ∂y∂f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ∂y∂f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
{∂f1 |
( |
|
|
x |
|
|
f |
|
|
) +( |
∂y1 |
+ |
|
|
∂z |
|
|
signf |
|
|
|
)( |
|
|
f |
|
f |
|
|
) + |
|
|
∂z |
|
|
signf |
|
|
( |
|
|
|
f |
|
|
|
)2}/ Q2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∂f |
|
|
|
|
|
|
∂f |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
∂f |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
В случае постоянных функций преобразования выражения |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
упрощаются, и можно записать в линейном приближении |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
y |
|
|
|
= |
|
|
|
f1x + f12 x |
|
|
|
f2 |
|
signf2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.23) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
(1) |
|
|
|
|
|
|
(1− f1 f2 signf2 )2 |
|
|
|
|
|
|
|
|
|
+ (1− f1 f |
2 signf2 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где signf2 =1 |
|
|
для положительной обратной связи и signf2 |
= −1 |
для |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отрицательной обратной связи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Соотношение |
|
|
|
|
|
|
|
|
|
|
для |
|
|
|
|
|
|
ошибки |
|
|
|
|
|
|
|
|
|
погрешности |
|
|
|
|
δ y |
мало |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
информативно, поэтому не приводится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
В квадратичном приближении имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 f2 |
|
|
f1 |
|
y(1) |
|
signf2 |
|
|
|
|
|
|
|
|
|
|
1 f |
f |
|
|
|
|
y(1) |
|
signf |
|
|
|
|
|
(3.1.24) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
y(2) |
= |
|
|
|
y(1) + |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
− f |
|
|
signf |
|
|
2 |
|
|
1− f |
|
f |
|
signf |
|
|
|
|
|
2 |
|
|
|
1− f |
|
f |
|
signf |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Определим математическое ожидание и дисперсию погрешности y из соотношения (3.1.24.)
M [ |
y] |
= xM [ |
f1 ]/ Q2 + f12 x |
|
signf2 |
|
M[ f2 ] / Q2 + S1M [ x]/ Q + |
|
|||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
+M [ f1 x] (1− 1 f1 f2 |
|
signf2 |
|
) / Q2 + |
1 M [ f2 |
x] f12 |
|
|
signf2 |
|
/ Q2 + |
|
|||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
1 M [ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 M ( |
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
f1 f2 ] f1xsignf2 (1+ f1 f2 |
|
signf2 |
|
) / Q3 + |
f1 )2 |
|
f2 x |
|
signf2 |
|
/ Q3 + |
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ |
1 M[( |
f2 )2 ] f13 x / Q3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.25) |
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D[ |
y]= x2 D[ |
f1 ]/ Q4 + f14 x2 D[ f2 ]/ Q4 + S12 D[ |
x]/ Q2 + |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
+ |
1 |
f22 x |
2 D ( f1 )2 / Q6 |
+ 1 |
|
f16 x2 D ( |
f2 )2 / Q6 + |
1 f14 D[ f2 x]/ Q4 |
|
||||||||||||||||||||||||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
1 |
f12 x2 D[ f1 |
f2 ](1+ f1 f2 |
|
signf2 |
|
)2 / Q6 + D[ |
f1 |
x](1− 1 f1 f2 |
|
signf2 |
|
)2 / Q4 . |
(3.1.26) |
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Q=1- |
В |
|
соотношениях |
(3.1.25, |
|
|
3.1.26) |
введено |
|
обозначение |
||||||||||||||||||||||||||||
f1f2signf2 и учтено, что (signf2 )2 =1.
Определим относительную погрешность. Для рассматриваемой схемы связь между входом и выходом представима в виде (см.§1.3.):
|
f1 x |
|
|
|
|
|
|
|
|
|
y = |
|
. |
|
|
|
|
|
|
|
(3.1.27) |
1 − f1 f2 signf2 |
|
|
|
|
|
|
|
|||
|
Из соотношений (3.1.24) и (3.1.27) после преобразований |
|||||||||
получим: |
1 |
|
|
|
|
|
|
|
||
δ y =δ y(1) +δ xδ f1 + |
δ y(1) |
f1 f2 |
|
signf2 |
|
(δ f1 +δ f2 ) / Q , |
(3.1.28) |
|||
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
где δ y(1) - относительная погрешность сигнала на выходе в линейном приближении
δ y(1) = (δ f1 + f1 f2 |
|
signf2 |
|
δ f2 ) / Q +δ x . |
(3.1.28а) |
|
|
Для математического ожидания и дисперсии относительной погрешности имеем соответственно:
M[δ y] = M[δ f1]/ Q + f1 f2 |
|
signf2 |
|
M[δ f2 ]/ Q +M[δ x]+ |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
+ |
1 |
f |
f |
signf |
M[(δ f )2 ]/ Q2 + |
1 f f |
|
|
signf |
|
|
|
(1+ f |
f |
|
|
signf |
|
|
)M[δ f δ f |
|
]/ Q2 |
+ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2 |
1 |
2 |
2 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
|
2 |
|
|
|
|
1 |
|
2 |
|
|
|
|
2 |
|
1 |
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
+ |
1 |
f 2 f |
2 M[(δ f |
|
)2 |
]/ Q2 + M[δ f δ x](1+ |
1 |
|
f f |
|
|
signf |
|
|
|
) / Q + |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2 |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
1 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
+ |
1 M[δ f2δ x] f1 f2 |
|
signf2 |
|
/ Q , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.29) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D[δ y] = D[δ f ]/ Q2 + f 2 |
f 2 D[δ f |
2 |
]/ Q2 |
+ D[δ x] + |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ |
1 |
D[(δ f )2 ] f 2 |
f 2 |
/ Q4 + |
1 |
f 4 |
f 4 D[(δ f |
|
)2 ]/ Q4 + |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
4 |
|
|
1 |
1 |
|
2 |
|
|
|
4 |
1 |
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

1 D[δ f |
δ f |
2 |
] f 2 |
f |
2 |
(1 |
+ f |
f |
2 |
|
|
signf |
2 |
|
|
)2 / Q4 + D[δ f δ x] |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
4 |
|
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1+ 1 |
f1 f2 |
|
signf2 |
|
)2 / Q2 + |
1 |
|
|
D[δ f |
2δ x] f12 f2 |
2 / Q2 . |
|
(3.1.30) |
||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
= const(i), |
то |
выражения |
для |
||||
|
Если |
|
|
|
|
|
положить |
|
|
|
|
|
|
δfi |
|||||||||||||||||||||||||||||
математического ожидания и дисперсии упрощаются: |
|
||||||||||||||||||||||||||||||||||||||||||
M [δ y]= (1+ f1 f2 |
|
|
signf2 |
|
|
)M [δ f1 ]/ Q + M [δ x]+ |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
(1+ f |
f |
2 |
|
signf |
2 |
|
) f |
|
f |
2 |
|
|
signf |
2 |
|
|
|
|
M[(δ f )2 |
]/ Q2 + |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
+M[δ f1δ x](1+ f1 f2 |
|
|
signf2 |
|
|
|
) / Q , |
|
|
|
|
|
|
|
|
|
|
(3.1.29а) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
D[δ y] = (1+ f12 f22 )D[δ f1 ] / Q2 + D[δ x]+ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
+ 1 D[(δ f )2 ]( f 2 f 2 |
+ f 3 |
|
f |
3 |
|
|
|
signf |
2 |
|
+ f 4 |
f 4 ) / Q4 + |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
2 |
|
|
1 |
|
|
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 f12 |
|
|
|
|
2 ) / Q2 . |
|
|
(3.1.30а) |
|||||||||
D[δ f1δ x](1+ f1 f2 |
|
signf2 |
|
+ |
|
|
f |
2 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если к тому же погрешность входного сигнала пренебрежимо мала (δ x = 0) , то выражения для математического ожидания и дис-
персии преобразуются к виду
M [δ y]= |
1+ f1 f2 |
|
signf2 |
|
M [δ f |
] |
+ f1 f2 |
|
signf2 |
|
(1+ f1 f2 |
|
signf2 |
|
) |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1− f1 f2 signf2 |
|
1 |
|
|
|
|
|
|
(1− f1 f2 signf2 )2 |
|
(3.1.29б) |
||||||||||||||
M[(δ f1 )2 ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D[δ y]= |
|
1+ f 2 f 2 |
2 )2 D[δ f1 |
]+ |
1 |
f12 f22 (1+ f1 f2 |
signf2 |
|
+ f12 f22 ) |
|
|||||||||||||||||
|
|
||||||||||||||||||||||||||
(1− f1 f2 signf |
2 |
|
|
(1− f1 f |
2 signf2 |
|
)4 |
|
|||||||||||||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
D (δ f1 )2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.30б) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из соотношений (3.1.29б, 3.1.30б) следует, что при f1=f2=1 и signf2=−1(отрицательная обратная связь) M [δy] в линейном приближении, вообще говоря, не равно нулю и зависит от M [δ f1 ];
этот вывод справедлив и в квадратичном приближении; для дисперсии имеем D[δy]= D[δf1 ] 2 , т.е. результат получается таким же, как и в параллельной схеме с двумя элементами. При положительной обратной связи, когда f1=f2=1 и signf2=1, M [δy] и D[δy] не определены, а именно, M [δy]→ ∞ и D[δy] → ∞ . Их конечность можно обеспечить только при M[δf ] = 0 и D[δf ]= 0 .
2 , т.е. результат получается таким же, как и в параллельной схеме с двумя элементами. При положительной обратной связи, когда f1=f2=1 и signf2=1, M [δy] и D[δy] не определены, а именно, M [δy]→ ∞ и D[δy] → ∞ . Их конечность можно обеспечить только при M[δf ] = 0 и D[δf ]= 0 .
Полученные соотношения для погрешности выходного сигнала типовых схем позволяют провести анализ и расчет погрешности
измерения для СИ, имеющих сложную структуру, которая представлена в виде комбинации типовых структур.
Рассмотрим в качестве примера измерительную систему на нейронных сетях (см. §1.3).Каждый нейрон сети представляет собой систему с многими входами и одним выходом (см. рис.13г), и погрешность преобразования рассчитывается из соотношений (3.1.22), (3.1.22а). Первый слой является параллельным объединением m нейронов, на вход каждого из которых подается n сигналов. Второй слой (скрытый) состоит из p нейронов, на вход каждого из которых подается m сигналов, содержащих погрешности y(j1) , с выходов нейронов 1-го слоя. На
выходе каждого нейрона скрытого (2-го) слоя получается сигнал,
содержащий суперпозицию погрешностей y(j1) и |
yq(2). На вход |
|||
каждого нейрона |
третьего |
слоя |
подается |
p сигналов, |
содержащих погрешности y(j1) и |
yq(2) |
с выходов нейронов 1-го и |
||
2-го слоев. На выходе каждого нейрона 3-го слоя получается сигнал, содержащий суперпозицию погрешностей y(j1) , yq(2) и
yr(3) , где |
y(j1) - погрешность преобразования при прохождении |
||||
первого |
слоя, |
определяемая соотношениями (3.1.22) |
или |
||
(3.1.22а); |
j = |
|
; |
yq(2) - погрешность преобразования |
при |
1, m |
|||||
прохождении второго (скрытого слоя), определяемая аналогично
первому слою; |
q = |
|
; yr(3) |
- погрешность преобразования при |
||
1, p |
||||||
прохождении |
сигналом |
3-го слоя; r = |
|
. В линейном |
||
1,l |
||||||
приближении, используя соотношение (3.1.22), имеем систему уравнений
n |
(3.1.31а) |
y(j1) = ∑S (j1)(i ) x(ji ) - для первого слоя, |
i=1
m
yq(2) = ∑Sq(2)(u) yq(u) - для второго слоя, (3.1.31б)
u=1
где yq(u )- погрешность сигнала на входе нейрона q 2-го слоя, получившаяся на выходе нейрона u 1-го слоя
p
yr(3) = ∑Sr(3)(υ) yr(υ) - для 3-го слоя, (3.1.31в)
υ=1
где yr(υ) - погрешность сигнала на входе нейрона r 3-го слоя, получившаяся на выходе нейрона υ 2-го слоя.
Из приведенных уравнений видно, что погрешность сигнала на выходе нейронной сети (погрешность
преобразования) зависит от погрешности сигнала на выходе каждого нейрона 1-го и 2-го слоев.
Пример 1. Оценим погрешность функционирования измерительной системы на нейронных сетях с учетом погрешности входного сигнала и погрешности преобразования. Используем результаты § 1.3. Обозначим, как и выше, j=1,…,m - число нейронов в первом (входном) слое, q=1,…,p - число нейронов во втором (скрытом) слое, r=1,…,l - число нейронов в третьем слое. Модель отдельного нейрона представляет собой последовательное соединение сумматора n→1 (много входов – один выход), персептрона и точки ветвления. Примем, что сумматор вычисляет линейную функцию входов
n
gx ≡ g(x) =∑ai xi +an+1 , (3.1.32)
i=1
где параметр an+1 соответствует аддитивной погрешности, а некоторые параметры ai могут равняться нулю. Для персептрона используем сигмоидальную функцию преобразования
f (x) =(1+exp(−kx))−1 . |
|
|
(3.1.33) |
||
Для |
нейрона |
первого |
слоя сети |
погрешность на выходе |
|
сумматора дается следующим соотношением |
|||||
z j |
n |
n |
|
|
|
=∑S(1)(j i) |
x(ji) +∑ g(1)(j |
i) , |
(3.1.34) |
||
|
i=1 |
i=1 |
|
|
|
где |
xj(i) – погрешность |
сигнала i |
на входе нейрона j; Sj(i) – |
||
чувствительность сумматора нейрона j по входному сигналу i; вторая сумма определяет погрешность преобразования, вызванную отклонением реальной функции преобразования сумматора от номинальной. В общем случае она представима в виде
gx ≡ g(x) −g0(x) = g(0) +(∂Δg / ∂x)0 x +.... |
(3.1.35) |
В линейном приближении учитываются только два первых члена, т.е. аддитивная и мультипликативная составляющие. Для zj имеем (индекс (1) опущен)
n |
n |
|
z j =∑S(ji) |
x(ji) +∑(a(ji) −a(ji0))x(ji) +an+1 . |
(3.1.36) |
i=1 |
i=1 |
|
Сигнал zj + zj поступает на вход персептрона, |
на выходе |
которого получаем |
|
yj = f (z j +Δz j ) =(1+exp(−k j (z j +Δz j )))−1. |
(3.1.37) |
Используя разложение в ряд с точностью до членов, линейных по zj, получим для сигнала на выходе с учетом погрешности сигнала на входе
y j = f j z j (1+k j z j ) , |
(3.1.38) |
где fjzj≡fj(zj)≡fj. Если учесть также составляющую, обусловленную погрешностью преобразования, то суммарная погрешность сигнала на выходе нейрона j первого слоя дается выражением
y(1)j |
=k(1)j f j(1) |
z(1)j |
+Δf j(1) z(1)j . |
|
|
|||||
Здесь |
|
|
|
|
|
|
|
|
|
|
f j(1) z(1)j = f j(1) (1− f j(1) )(k(1)j |
−k(1)j0 )z(1)j , |
|
|
|||||||
|
n |
i)x(1)(j |
i) +an(1)(+1 j) |
|
|
|
|
|||
z(1)j =∑a(1)(j |
, |
|
|
|
||||||
|
i=1 |
|
|
|
|
n |
|
|
|
|
z(1)j |
n |
|
|
x(1)(j |
|
i) −a(1)(j0 |
i))x(1)(j |
i) +an(1)(+1 j) . |
||
=∑S(1)(j |
i) |
i) +∑(a(1)(j |
||||||||
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
(3.1.39)
(3.1.39а)
(3.1.39б)
(3.1.39в)
Из выражения (3.1.39) следует, что погрешность сигнала на выходе зависит от входного сигнала и его погрешности. Для второго слоя имеем
y(2) |
=k(2) f |
(2) |
z(2) |
+Δf (2) z |
(2) . |
|
(3.1.40) |
||
q |
|
q |
q |
q |
q |
q |
|
|
|
Здесь |
|
|
|
|
|
|
|
|
|
f (2) z(2) |
= f |
(2) (1− f (2))(k |
(2) |
−k(2) )z(2) , |
(3.1.40а) |
||||
q |
q |
|
q |
|
q |
q |
q0 |
q |
|
|
m |
|
|
|
|
|
|
|
|
zq(2) =∑bq(2)(u) yq(2)(u) +bm(2)(+1q) , |
|
|
(3.1.40б) |
||||||
|
u=1 |
|
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
|
||
zq(2) =∑Sq(2)(u) |
yq(2)(u) +∑(bq(2)(u) −bq(2)(0 u))yq(2)(u) +bm(2)(+1q) , |
(3.1.40в) |
|||||||
|
u=1 |
|
|
u=1 |
|
|
|
||
где |
yq(2) – погрешность |
сигнала на выходе нейрона q |
второго |
||||||
слоя; |
yq(2)(u) – погрешность сигнала на входе нейрона q второго |
||||||||
слоя, получившаяся на выходе нейрона u первого слоя; yq(2)(u) – |
|||||||||
сигнал |
на входе нейрона q второго слоя с выхода нейрона u |
||||||||
первого слоя
y(2)(u) |
= f (1) z(1) |
, |
(3.1.40г) |
|
q |
|
u u |
|
|
где zu(1) |
дается выражением (3.1.39б); а |
yq(2)(u) – выражением |
||
(3.1.39), при этом следует положить j=u. Аналогично для
погрешности |
сигнала |
на |
выходе |
нейрона r третьего слоя |
||||||
(погрешности результата измерения) можно записать |
|
|||||||||
y(3) |
=k(3) f |
(3) |
z(3) +Δf (3) z(3) . |
|
|
|
(3.1.41) |
|||
r |
r |
r |
r |
r |
r |
|
|
|
|
|
Здесь |
|
|
|
|
|
|
|
|
|
|
f (3) z(3) = f |
(3) |
(1− f (3))(k(3) |
−k(3))z(3) , |
|
|
(3.1.41а) |
||||
r |
r |
r |
r |
r |
|
r0 |
r |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
zr(3) =∑cr(3)(v) yr(3)(v) +c(3)(p+1r) , |
|
|
|
|
|
(3.1.41б) |
||||
|
v=1 |
|
|
|
|
|
|
|
|
|
|
p |
|
|
p |
|
|
|
v))yr(3)(v) +c(3)(p+1r) , |
|
|
zr(3) =∑Sr(3)(v) yr(3)(v) +∑(cr(3)(v) −cr(3)(0 |
(3.1.41в) |
|||||||||
|
v=1 |
|
|
v=1 |
|
|
|
|
|
|
где |
yr(3) – погрешность |
сигнала на выходе нейрона |
r третьего |
|||||||
слоя; |
yr(3)(v) – |
погрешность сигнала на входе нейрона r третьего |
||||||||
слоя, получившаяся на выходе нейрона v |
второго слоя; yr(3)(v) – |
|||||||||
сигнал на входе нейрона |
r |
третьего слоя с выхода нейрона v |
||||||||
второго слоя |
|
|
|
|
|
|
|
|
||
y(3)(v) = f (2) z(2) , |
|
|
|
|
|
|
(3.1.41г) |
|||
r |
v |
v |
|
|
|
|
|
|
|
|
где |
zv(2) и |
yr(3)(v) даются |
выражениями |
(3.1.40б) |
и (3.1.40) |
|||||
соответственно, при этом следует положить q= v. |
|
|||||||||
Пример 2. Пусть входные сигналы xi, поступающие на вход нейронной сети, являются нечеткими, т.е. представимы в виде нечетких чисел или нечетких интервалов. Функции преобразования сумматора и персептрона также будем считать нечеткими, что позволяет учесть неопределенность (погрешность) преобразования, используя соответствующий способ задания сигналов и функций. В этом случае выходной сигнал получается нечетким и содержит неопределенность, обусловленную нечеткостью входного сигнала и параметров нейронной сети. Рассмотрим цепочку преобразований на входе
~
нейрона j первого слоя сети. Определим нечеткую функцию g(x)
из соотношения (3.1.32). Сначала вычислим произведения вида ai~xi . Имеем для i=1
μ |
~ |
(o(1 j)) = |
|
sup |
|
min(μ~ |
(u(1 j)),μ~ |
(v(1 j))) . |
|
|
a1x1 |
1 |
(1 j) |
(1 j) (1 j) |
a1 |
1 |
x1 |
1 |
|
|
|
|
o1 |
=u1 |
v1 |
|
|
|
|
нечеткие
(3.1.42а)
Здесь и далее мы будем использовать операции sup и min для объединения и пересечения, хотя возможны и другие пары операций, например, sup• (• -произведение), inf sum и т.д. Аналогично для произвольного i можно записать
μ ~ (o(1 j) ) = |
|
sup |
|
min(μ~ (u(1 j)),μ~ (v(1 j) )) , |
(3.1.42б) |
||||||||
|
aixi |
i |
(1 j) |
|
(1 j) (1 j) |
ai |
i |
xi |
i |
|
|||
|
|
|
oi |
=ui |
vi |
|
|
|
|
|
|
||
Наконец, для i=n |
|
|
|
|
|
|
|
|
|||||
μ |
~ |
(o(1 j)) = |
|
sup |
|
(1 j) |
min(μ ~ |
(u(1 j)),μ~ |
(v(1 j))). |
(3.1.42в) |
|||
|
anxn |
n |
(1 j) |
=u |
(1 j) |
an |
n |
xn |
n |
|
|||
|
|
|
o |
|
|
v |
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
n |
|
|
|
|
|
|
Теперь определим операцию суммирования
μ
μ
~
g2(1 j)
~
gi(1 j)
(t2(1 j)
(ti(1 j)
) =
) =
sup
t2(1 j)=o1(1 j)+o2(1 j)
sup
ti(1 j)=ti(1−1j)+oi(1 j)
min(μ ~ (o(1 j)
a1x1 1
min(μ ~ (t(1 j)
gi(1−1j) i−1
),μ |
~ |
(o(1 j))), |
|
|
a2x2 |
2 |
|
),μ ~ |
(o(1 j))) , |
||
|
aixi |
i |
|
(3.1.43а)
(3.1.43б)
|
|
~ |
~ |
|
|
|
|
|
|
|
где i=2,…,n; g1 |
=a1x1 |
. На выходе сумматора получается нечеткий |
||||||||
сигнал, определяемый выражением |
|
|
|
|
||||||
μ ~ |
(t(1 j)) = |
sup |
|
min(μ ~ |
(t(1 j)),μ |
a |
~ |
(u(1 j) )). |
(3.1.44) |
|
g |
(1 j) |
n+1 |
|
|
(1 j) |
n |
|
n+1 |
|
|
n+1 |
t(1 j) =t(1 j) +u(1 j) |
gn |
|
n+1 |
|
|
||||
|
n+1 |
n |
n+1 |
|
|
|
|
|
|
|
Этот сигнал поступает на вход персептрона с нечеткой функцией преобразования вида (3.1.33). Имеем цепочку соотношений
μ |
~ |
(ρ(1 j)) = |
sup |
min(μ ~ |
(ρ(1 j)),μ |
~ |
(t(1 j))) , (3.1.45) |
||
k |
(1 j) |
|
(1 j) |
ρ(1 j) =ρ1(1 j) tn(1+1j) |
k |
(1 j) |
1 |
(1 j) |
n+1 |
|
gn+1 |
|
|
gn+1 |
|
||||
μ |
~ |
(ω(1 j)) = |
sup |
min(1,μ |
~ |
(ρ(1 j))) , |
(3.1.46) |
|
−k(1 j)g(1 j) |
ω(1 j)=−ρ(1 j) |
k(1 j)g(1 j) |
|
|||
|
n+1 |
|
|
|
n+1 |
|
|
μ |
~ |
(ω(1 j)) = |
|
sup |
|
|
exp(−k(1 j)gn(1+1j) ) |
|
1 |
ω1(1 j) =exp(ω(1 |
|
|
|
|
|||
μ |
~ |
|
(ω(1 j)) = |
sup |
|
1+exp(−k(1 j)gn(1+1j) ) |
2 |
|
ω2(1 j) =1+ω1(1 |
||
|
|
||||
|
min(1,μ |
|
~ |
(1 j) |
(ω(1 j))) , (3.1.46а) |
||
j) ) |
−k |
(1 j) |
|
|
|||
|
gn+1 |
|
|
||||
|
min(1,μ |
|
|
~ |
|
(ω(1 j))) . |
|
j) |
exp(−k |
(1 j) |
|
(1 j) |
1 |
||
|
|
gn+1 ) |
|
||||
(3.1.46б)
Выходной сигнал нейрона j первого слоя сети дается выражением
μ ~ (w(1 j)) = |
sup |
min(1,μ |
~ |
(ω2(1 j))) , |
(3.1.47) |
y j |
w(1 j) =(ω2(1 j) )−1 |
1+exp(−k(1 j)gn(1+1j) ) |
|
|
|
где j=1,2….m;
~
y~ j =(1+exp(−k(1 j)
m-число |
нейронов |
в |
первом |
|||
~ |
~ |
|
+...+a |
|
~ |
|
g(1 j)))−1 |
; g(1 j) =a~x |
~x ; g(1 j) |
||||
n+1 |
n |
1 1 |
|
n n |
n+1 |
|
слое |
сети; |
|
~ |
|
. |
=g(1 j) + a~ |
||
n |
n+1 |
|
Отметим, что соотношения (3.1.42а –3.1.47) могут быть записаны в альтернативной форме через α-срезы соответствующих нечетких множеств. Сигналы вида (3.1.47) с выходов нейронов первого слоя подаются на вход каждого нейрона второго слоя сети. Имеем цепочку преобразований,
аналогичную таковой для первого слоя с заменой индексов и |
|||||||||
обозначений: (1j)→(2q); n→m; |
~ |
~ |
; |
~ |
~ |
|
~ |
~ |
|
a |
→b |
j |
x |
→ y |
j |
; k(1 j) →k(2q) . |
|||
|
i |
|
|
i |
|
|
|
||
На выходе нейрона q второго слоя сети получаем сигнал, определяемый соотношением
μ~ (w(2q)) = |
|
sup |
min(1,μ |
~ |
|
(ω2(2q))) , |
(3.1.48) |
|
zq |
w(2q) =(ω2(2q) )−1 |
1+exp(−k(2q)gm(2+q1) ) |
|
|
||||
где q =1,…,p; |
|
~ |
~ |
; |
~ |
=b~y |
+...+b ~y ; |
|
z~ =(1+exp(−k(2q) g(2q)))−1 |
g(2q) |
|||||||
|
|
q |
|
m+1 |
|
m |
1 1 |
m m |
~ |
~ |
|
. |
g(2q) =g(2q) +b ~ |
|||
m+1 |
m |
m+1 |
|
Сигналы |
вида (3.1.48) с выходов нейронов второго слоя |
||
подаются на вход каждого нейрона третьего слоя. Выражение для сигнала на выходе нейрона r третьего слоя получается из
соотношений |
типа (3.1.42а – |
3.1.47) |
с заменой |
индексов |
и |
||||
обозначений |
|
~ |
~ |
~ |
~ |
~ |
~ |
В |
|
(1j)→(3r); n→p; a |
→c |
; x |
→ z ; |
k(1 j) →k(3r) . |
|||||
итоге получаем |
i |
r |
i |
r |
|
|
|
||
|
|
|
|
|
|
|
|||
μ~ (w(3r)) = |
|
sup |
min(1,μ |
|
~ |
(ω2(3r))) , |
(3.1.49) |
||
vr |
w(3r) =(ω2(3r) )−1 |
1+exp(−k(3r)g(3p+r1) ) |
|
|
|
||||
где r =1,…,l; v~r =
~ = ~ ~
g(3p+r1) g(3p r) +cp+1 .
~ ~ |
; |
~ |
|
+...+c |
~z |
|
; |
(1+exp(−k(3r) g(3r)))−1 |
g(3r) =c~z |
p |
|||||
p+1 |
|
p |
1 1 |
|
p |
|
|
Выражение (3.1.49) позволяет определить сигнал на выходе нейронной сети (результат измерения) и его неопределенность, зависящую от неопределенности нечетких входных сигналов и нечетких параметров сети. Достоверность результата измерения (3.1.49) определяется сравнением с индексом нечеткости ν
~
множества vr . Результат считается достоверным, если
μ~ (w) >ν .
vr
Таким образом, в случае четких входных сигналов погрешность сигнала на выходе любого нейрона третьего слоя сети (погрешность результата измерения) зависит от выходных сигналов (и их погрешностей) всех нейронов предыдущих слоев. В нечетком случае функция принадлежности, характеризующая выходной сигнал и его неопределенность, зависит от функций принадлежности выходных сигналов нейронов предыдущих слоев.
