3.3. Частотные характеристики звеньев

Важнейшей характеристикой динамического звена является его частотная передаточная функция. Для получения её рассмотрим случай, когда при ΔF= 0 (см. рис. 3.1) на входе звена имеется гармоническое воздействие x₁ =X₁sint, гдеX₁– амплитуда, а– угловая частота этого воздействия. Тогда на выходе звена в установившемся режиме будет также гармоническая функция той же частоты, но в общем случае сдвинутая по фазе относительно входной величины. Таким образом, для выходной величины можно записать x₂= X₂ sin(t+).

Воспользуемся символической записью гармонических функций:

(3.11)

Символичность записи заключается в том, что на самом деле левые части (3.11) равны мнимой составляющей правых частей, то есть

(3.12)

Однако для сокращения записи используют сокращенную «символическую» форму (3.11).

Для нахождения соотношения между выходной и входной гармоническими величинами звена воспользуемся его дифференциальным уравнением

. (3.13)

Из (3.11) определим производные:

. (3.14)

Подставив значения входной и выходной величин и их производных в исходное дифференциальное уравнение, получаем

(3.15)

Откуда после сокращения на общий множитель имеем

. (3.16)

Это выражение называется частотной передаточной функцией звена. Таким образом, частотная передаточная функция представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к входной, а аргумент – сдвигу фаз выходной величины по отношению к входной.

Из выражения для частотной передаточной функции видно, что она может быть легко получена из передаточной функции звена (3.2) подстановкой p = ω, то есть.

Частотная передаточная функция звена есть изображение Фурье его функции веса, то есть имеет место интегральное уравнение

. (3.17)

Частотная передаточная может быть представлена как

, (3.18)

где A(ω) – модуль частотной передаточной функции;(ω) – аргумент или фаза частотной передаточной функции;u(ω) иv(ω) – вещественная и мнимая части частотной передаточной функции.

Модуль находится как модуль числителя частотной передаточной функции, деленный на модуль знаменателя. Для рассмотренного выше примера (3.2) имеем:

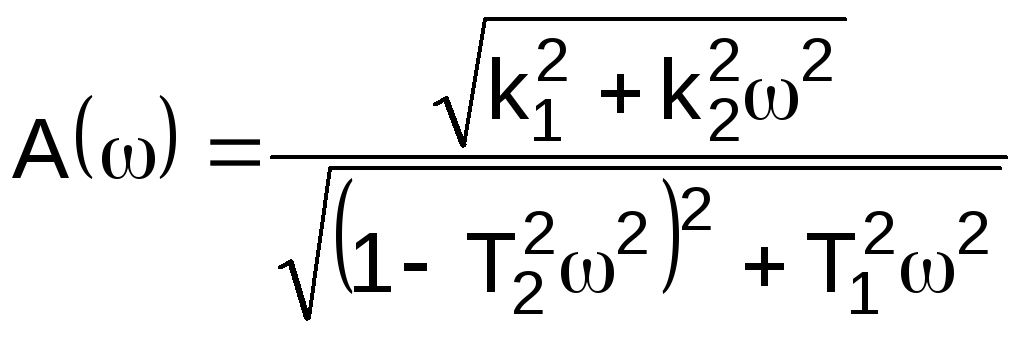. (3.19)

Аргумент или фаза частотной передаточной функции находится по разности аргументов числителя и знаменателя. Для (3.2) имеем:

. (3.20)

Для нахождения вещественной и мнимой частей частотной передаточной функции необходимо освободиться от мнимости в знаменателе последней. Для этой цели числитель и знаменатель частотной передаточной функции необходимо умножить на комплекс, сопряженный знаменателю. Так, для рассматриваемого примера имеем

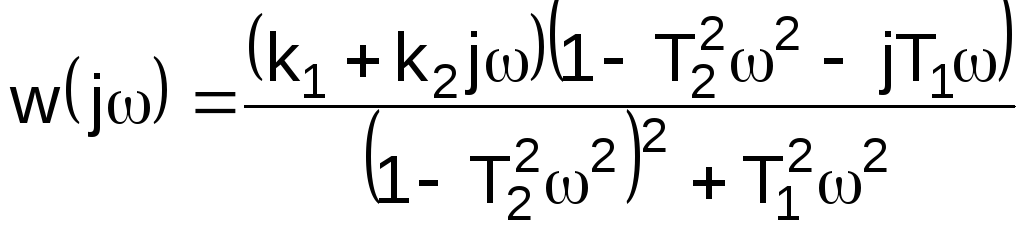. (3.21)

Откуда после разделения на вещественную и мнимую части получаем

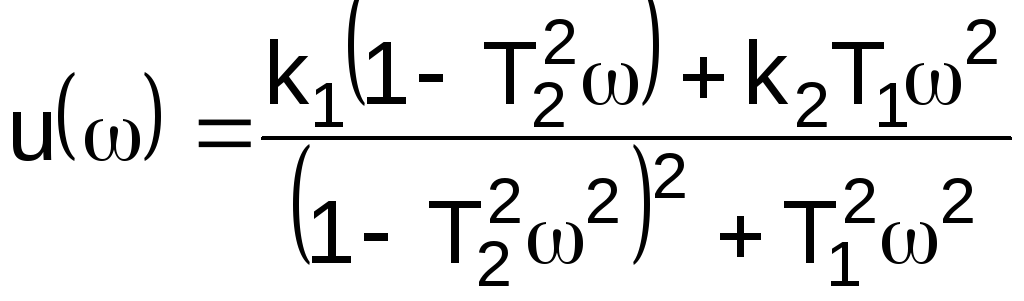; (3.22)

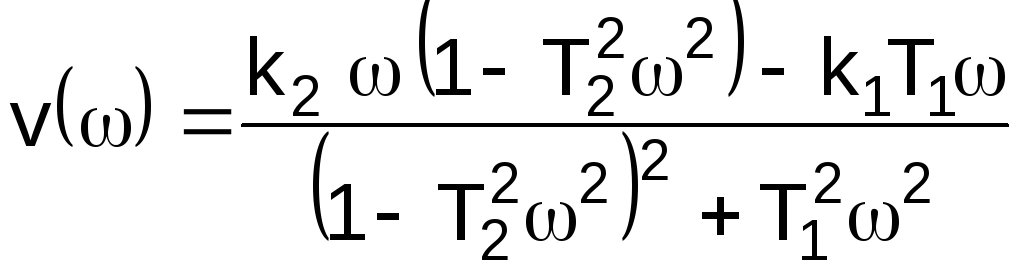. (3.23)

Д

Рис. 3.6. Построение АФЧХ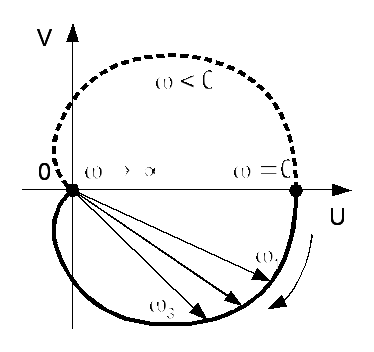

ля наглядного представления частотных свойств звеньев используются так называемые частотные характеристики.

Амплитудно-фазовая частотная характеристика(АФЧХ) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих комплексу частотной передаточной функции при изменении частоты от нуля до бесконечности (рис. 3.6). По оси вещественных откладываетсяu(ω), а по оси мнимых v(ω). Задаваясь различными значениями частоты в пределах 0 < ω < ∞, можно составить табл. 3.1.

Таблица 3.1

АФЧХ для декартовых координат

ω	U(ω)	V(ω)
0 … ∞	– – –	– – –

Затем наносим точки на комплексной плоскости и соединяем их плавной кривой. Около нанесенных точек можно написать соответствующие им частоты.

АФЧХ может быть построена и для отрицательных частот. При замене в частотной передаточной функции +ω на –ω получим сопряженный комплекс. Поэтому АФЧХ для отрицательных частот может быть построена, как зеркальное изображение АФЧХ для положительных частот относительно горизонтальной оси – вещественных значений. На рис. 3.6 АФЧХ для отрицательных частот показана пунктирной линией.

Модуль вектора, проведенного из начала координат в точку годографа, соответствующую какой-то выбранной частоте, равен модулю частотной передаточной функции. Угол между вектором и положительным направлением вещественной оси, отсчитываемый против часовой стрелки, равен аргументу или фазе частотной передаточной функции. Таким образом, АФЧХ дает возможность увидеть для каждой частоты входного воздействия звена как отношение амплитуд выходной и входной величин, так и сдвиг фаз между ними.

Построение АФЧХ по вещественной и мнимой частям частотной передаточной функции, как правило, является трудоемкой работой, так как умножение частотной передаточной функции на комплекс, сопряженный её знаменателю, повышает в два раза степень частоты в знаменателе. Это можно увидеть из выражений (3.22) и (3.23). Обычно гораздо проще строить АФЧХ, используя полярные координаты, то есть, вычисляя непосредственно модуль и фазу. Для этой цели составляется таблица, аналогичная табл. 3.2.

Зная модуль и фазу вектора, можно легко построить соответствующую точку на комплексной плоскости. В случае необходимости при известных модуле и фазе можно вычислить вещественную и мнимую части умножением модуля на направляющий косинус между вектором и соответствующей осью.

Таблица 3.2

АФЧХ для полярных координат

ω	A(ω)	(ω)
0 … ∞	– – –	– – –

Вместо АФЧХ можно построить отдельно амплитудную частотную характеристику (АЧХ) ифазовую частотную характеристику(ФЧХ). Это построение делается по табл. 3.2 (рис. 3.7).

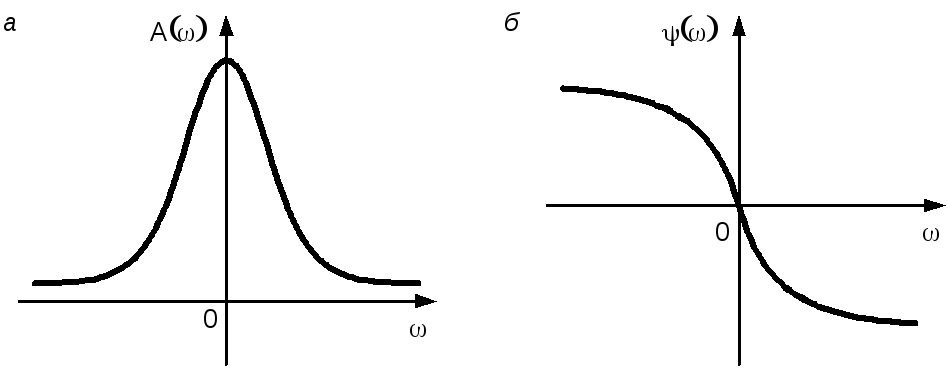
Рис. 3.7. Пример АЧХ (а) и ФЧХ (б)

Амплитудная частотная характеристикапоказывает, как звено пропускает сигнал различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазовая частотная характеристикапоказывает фазовые сдвиги, вносимые звеном в сигнал на различных частотах.

По результатам вычисления модуля и фазы для положительных частот можно сразу построить АЧХ и ФЧХ для всего диапазона частот от -∞ до +∞ аналогично АФЧХ.

Иногда строятся также вещественная и мнимая частотные характеристики. Это построение делается по данным табл. 3.1. Вещественная характеристика представляет собой четную функцию частоты, а мнимая характеристика – нечетную функцию частоты.