
Прикл мех
.pdf
|
|
|
1 |
|
|
l |
|
|
|
||
|
1 |
|
|
|
|
|
|
, |
|||
|
|
|
l |
|
|||||||
1 |
|
|
u |
|
l |
p |
|||||
|
|
|
12 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
l |
|
|
|
||
|
1 |
|
|
|
|
|
. |
||||
|
|
|
l |
|
|||||||
2 |
|
|
u |
|
l |
p |
|||||
|
|
|
12 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
де l – відстань від полясу зачепленнѐ Р до поточного положеннѐ точки контакту пари зубців,
lр1, lр2 – довжини відрізків PN1, PN2.
г
н
З діаграми видно, що у полясі зачепленнѐ (Р) обидва коефіціюнта дорівняять нуля, максимальне значеннѐ коефіціюнта питомих
ковзань маю місце в момент входу і виходу із зачепленнѐ. Коефіціюнт питомих ковзань на голівці зубцѐ менше ніж на ніжці.
Коефіцієнт питомого тиску враховую вплив геометричних параметрів (радіусів кривизни їх профілів) на величину контактних напружень, ѐкі виникаять у місцѐх стисканнѐ. При великому навантаженні контактні напруженнѐ можуть бути значні, що викликаю викришуваннѐ матеріалу на робочій поверхні зубцѐ.
m ,
де m – модуль зачепленнѐ,
– приведений радіус кривизни евольвентних профілів у точці контакту
|
1 |
|
1 |
|
1 2 |
. |
|
|
|
||||
|
1 |
2 |
1 2 |
|||
Коефіцієнт форми зуба характеризую згинальну міцність зуба.
Кінематичні дослідження зубчастих механізмів
Зубчасті механізми здійсняять простий обертальний рух. Тому дослідженнѐ цього руху виконуять, ѐк правило, за допомогоя аналітичного методу, ѐкий враховую передаточні відношеннѐ.
Длѐ одніюї пари зубчастих коліс передаточне відношеннѐ визначаютьсѐ за формулоя:
i |
1 |
|
n1 |
|
d2 |
|
z2 |
|
|
|
|
|
|||||
12 |
2 |
|
n2 |
|
d1 |
|
z1 |
|
|
|
|
|
|||||
За допомогоя одніюї пари зубчастих коліс (циліндричної, конічної передачі) можливо реалізувати передаточне відношеннѐ до 6. Якщо треба реалізувати більше передаточне відношеннѐ використовуять складні зубчасті механізми, ѐкі розподілѐятьсѐ на:
механізми з нерухомими осѐми;
механізми, в ѐких деѐкі осі обертаятьсѐ навколо нерухомих осей (сателітні). Механізми з нерухомими осѐми:
ступінчасті,
рѐдові.
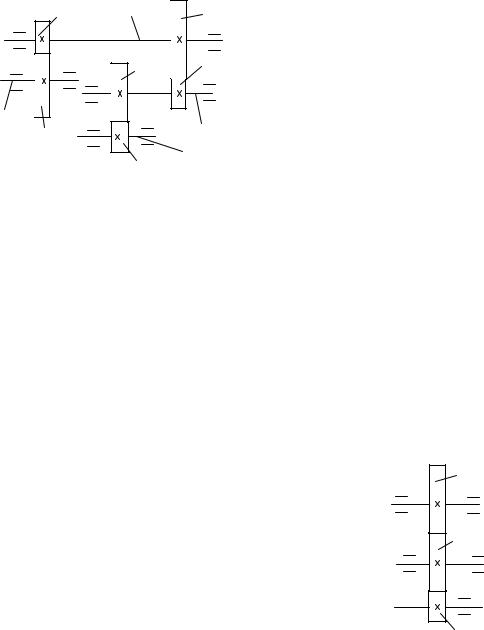
Ступінчасте зачеплення – колеса знаходѐтьсѐ в зачепленні попарно (стрілочний електропривод).
Передаточне відношеннѐ по ступенѐм:
|
|
|
|
|
|
|
i |
|
|
|
|
nI |
|
|
|
z2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
I II |
|
nII |
|
|
|
z1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
i |
|
|
nII |
|
z4 |
|
||||||||||||
|
|
|
|
|
|
|
II III |
|
|
nIII |
|
|
|
|
|
z3 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
i |
|
|
nIII |
|
z6 |
|
||||||||||||
|
|
|
|
|
|
|
III IV |
|
|
|
nIV |
|
|
|
|
|
z5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
i |
i |
i |
i |
|
nI |
|
nII |
|
nIII |
|
|
|
|
nI |
|
|
|
z2 z4 |
z6 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
I IV |
I II |
II III |
III IV |
|
nII |
|
nIII |
|
nIV |
|
|
|
|
nIV |
|
|
|
|
|
z1 z3 |
z5 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Загальне передаточне відношеннѐ ступінчастого механізму дорівняю добутку передаточних відношень окремих ступенів, або відношення добутку чисел зубців парних зубчастих коліс, добутку чисел зубців непарних зубчастих коліс.
Знак передаточного відношеннѐ: |
|
|
|
|
|
|
|
|
|
|
|
|
||
длѐ зовнішнього зачепленнѐ |
„ – „ |
|
|
|
|
|
|||
длѐ внутрішнього зачепленнѐ |
„ +” |
|
||
Коли кількість зовнішніх зачеплень непарне знак „–„, коли парне – „+”.
i |
|
z2 z4 z6 |
|
1 n . |
||||
|
|
|
|
|||||
I IV |
|
|
z1 z3 z5 |
|
|
|||
|
|
|
|
|
||||
Рядове зачеплення – загальне передаточне відношеннѐ дорівняю добутку |
||||||||
передаточних чисел окремих ступенів. |
|
|
|
|
|
|
|
|
i |
|
1 |
|
z3 |
|
1 n |
||
|
|
|||||||
I III |
|
3 |
|
z1 |
|
|
||
|
|
|
|
|
|
|||
Загальне передаточне відношеннѐ рѐдового зачепленнѐ залежить від кількості зубців крайніх механізмів. проміжні зубчасті колеса, ѐкі не впливаять на передаточне відношеннѐ, називаятьсѐ паразитарними.
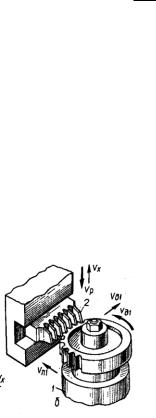
Методи виготовлення зубчастих коліс
Існуять два методи виготовленнѐ зубчастих коліс:
копіяваннѐ,
накатки,
обкатка.
При виготовленні методом копіювання використовуятьсѐ пальцева або дискова модульна фреза, профіль ѐкої відповідаю профіля западин зубчастого колеса. Обертаячись фреза переміщуютьсѐ в напрѐмку бокової утворяячої зубцѐ. За кожен крок фрези вздовж осі колеса
утворяютьсѐ нарізаноя одна западина. Післѐ цього колесо переміщуютьсѐ на кут 2z .
Потім процес повторяютьсѐ. Цей метод ю малопродуктивним і потребую великої кількості різального інструменту. До методів копіяваннѐ також належать: отливка, штампуваннѐ, протѐгуваннѐ, струганнѐ.
Метод накатки – зубчасте інструментальне колесо накатую зубці зубчастого колеса, матеріал ѐкого достатньо еластичний (у холодному чи гарѐчому стані). Використовуютьсѐ длѐ дрібномодульних коліс ( m 5
При методі обкатки длѐ нарізуваннѐ коліс використовуютьсѐ інструментальна рейка. Перевага в тому, що одним й тим самим інструментом можна виготовити колеса з будь-ѐкоя кількістя зубців загального модуля.
Метод обкатки (долбѐком, рейкоя, черв’ѐчноя фрезоя) полѐгаю втому, що ріжучому інструменту та заготівці надаять той відносний рух, ѐкий мали б зубчасті колеса будучи в зачепленні.
При нарізуванні долбѐком, долбѐк здійсняю рух паралельно осі перпендикулѐрної площині колеса. Водночас колесу та долбѐку надаять обертальний рух з тим самим відношеннѐм кутових швидкостей, ѐкби вони знаходились в зачепленні. Практично процес довбаннѐ здійсняютьсѐ не безперервно, а маю рѐд
послідовних операцій: долбѐк рухаютьсѐ вниз та вгору, колеса повертаютьсѐ; Ці рухи узгоджені з кінематичним співвідношеннѐм, ѐки визначаять долбѐк та колесо ѐк два колеса, ѐкі знаходѐтьсѐ в зачепленні. Цей метод дозволѐю нарізувати колеса з внутрішнім зачепленнѐм.
При нарізуванні інструментальноя рейкоя, рейка здійсняю у вертикальному напрѐмку зворотно-поступові рухи, паралельні осі колеса, що нарізуютьсѐ. Заготівка маю подвійний рух у горизонтальній площині: обертаячись навколо власної осі, вона водночас переміщуютьсѐ вздовж рейки. Цей процес виконуютьсѐ на спеціальних зуборізних станках.
Якщо при виготовленні зубчастого колеса середнѐ (ділильна) лініѐ рейки торкаютьсѐ ділильного кола заготовки колеса, то нарізуютьсѐ колеса без зміщеннѐ. Якщо середнѐ лініѐ рейки зміщуютьсѐ відносно центра заготовки нарізуятьсѐ колеса зі зміщеннѐм (додатне (від центру) – збільшуятьсѐ розміри колеса, товщина зубцѐ, зуб зміцняютьсѐ; від’юмне (до центру) – використовуютьсѐ длѐ зменшеннѐ міжосьової відстані, зменшеннѐ габаритів, можливе підрізаннѐ зубців ).
.

ДИНАМІКА
Динаміка - це розділ теоретичної механіки, в ѐкому вивчаятьсѐ закони руху матеріальних тіл в залежності від діячих на них сил.
Основні закони динаміки
(закони Галілеѐ-Ньятона).
1. Закон про інерцію (І закон Галілеѐ).
Матеріальна точка зберігаю стан спокоя або рівномірного прѐмолінійного руху до того часу, поки прикладені сили не змінѐть цей стан.
Інертність - намаганнѐ тіла зберігати незмінноя швидкість свого руху, тобто зберігати отриманий раніш механічний рух.
Рух, ѐкий створяю точка при відсутності сил, називаютьсѐ рухом за інерцією. Інерційними системами відліку (умовно нерухомими) називаять - системи відліку,
відносно ѐких відбуваютьсѐ рух тіл з плином часу і виконуютьсѐ закон інерції.
2. Закон пропорційності сили та прискорення (основний закон динаміки).
Прискореннѐ матеріальної точки пропорційне прикладеній силі і маю однаковий з нея напрѐмок.
F m a
Кількісноя міроя інертності матеріальної точки та тіла при поступальному русі ю її маса ( m ). Одиницея виміряваннѐ маси ю 1 кг.
Міроя інертності тіла при обертальному русі ю момент інерції J Z .
Момент інерції тіла відносно осі J Z (осьовий момент інерції) – скалѐрна величина, ѐка дорівняю сумі добутків мас всіх точок тіла (системи) на квадрати їх відстаней i до осі:
k
J Z (mn in2 ) ,
n 1
де i - радіус інерції тіла або точки тіла - відстань від точки до осі обертаннѐ.
Одиницея виміряваннѐ моменту інерції вважаять (кг м2).
3. Закон рівняння дії та протидії.
Кожній дії відповідаю рівна за модулем та протилежна за напрѐмком протидіѐ.
Диференційні рівняння вільної матеріальної точки.
|
|
Вільна матеріальна точка М відомої маси |
m , рухаютьсѐ під діюя системи |
сил |
||||||||||
F1 , |
|
|
|
, рівнодійна системи |
|
k |
|
|
|
|
|
|
||
F2 , |
... |
Fn |
F |
|
Fn |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k |
|
||
|
|
Прискореннѐ, що надаю система сил точці, |
ю сумарним вектором |
a |
|
an |
, |
ѐкий |
||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
||
спрѐмований за вектором рівнодійної. |
|
|
|
|
|
|
||||||||
Основне рівняння динаміки для системи сил:
m a F1 F2 ... Fn
Диференційні рівняння руху матеріальної точки:
|
|
|
|
|
|
k |
|
m x F1x F2 x ... Fnx |
Fnx |
||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
k |
|
m y F1y |
F2 y |
... Fny Fny |
|||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
k |
|
m z F1z |
F2 z |
... Fnz |
Fnz |
||
|
|
|
|
|
|
n 1 |
де x , |
|
|
|
|||
y , z - проекції прискореннѐ a на координатні осі, |
||||||
F1X , F1Y , F1Z , F2 X , F2Y , F2 z ....Fnx , Fny , Fnz - проекції сил F1 , F2 ,...Fn на координатні осі.
Дві задачі динаміки точки.
Перша задача динаміки (пряма).
Знаючи масу точки m та рівнѐннѐ її руху x f1 (t) , y f2 (t) , z f3 (t) , Визначити модуль і напрѐмок рівнодійної сил, прикладених до точки.
Рішення першої задачі динаміки проводитьсѐ методом подвійного диференціяваннѐ рівнѐнь руху за часом.
Диференційні рівнѐннѐ руху точки:
k
m x Fnx FX ,
n 1
k
m y Fny Fy ,
n 1
k
m z Fnz Fz
n 1
Модуль рівнодійної
F 
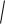 Fx2 Fy2 Fz2
Fx2 Fy2 Fz2
Напрѐмок рівнодійної:

|
|
|
F |
|
|
|
|
|
Fy |
|
|
|
|
|
F |
||
cos(F,i) |
cos(F, j) |
, cos(F, k) |
|||||||||||||||
x |
, |
|
z |
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
F |
|
|
|
|
|
F |
|
|
|
|
|
F |
||
Друга задача динаміки (обернена, основна).
Знаючи масу точки m , сили, що діять на точку, а також початкове положеннѐ ( X 0 ,Y0 , Z0 ) і
початкову швидкість ( X 0 ,Y 0 , Z0 ),
Визначити закон руху x f1 (t) , y f2 (t) , z f3 (t)
Рішення другої задачі динаміки здійсняютьсѐ методом інтегруваннѐ (подвійного за часом) диференційних рівнѐнь при відомих початкових умовах.
1. Складаннѐ диференційних рівнѐнь в виглѐді (3.3) в залежності:
m x FX (t, x, y, z, x , y , z ) m y FY (t, x, y, z, x , y , z ) m z FZ (t, x, y, z, x , y , z )
2.Інтегруваннѐ диференційних рівнѐнь руху двічі за часом.
3.Визначеннѐ постійних інтегруваннѐ за початковими умовами:
t0, x x0 , y y0 , z z0 , x x0 , y y0 , z z0
4.Отриманнѐ рівнѐнь руху точки:
x f1 x f (t, x0 , y0 , z0 , x0 , y0 , z0 )
y f |
2 |
(t, x |
0 |
, y |
0 |
, z |
0 |
, x |
, y |
, z ) |
|||
|
|
|
|
|
|
|
0 |
0 |
0 |
||||
z f |
3 |
(t, x |
0 |
, y |
0 |
, z |
0 |
, x |
, y |
, z ) |
|||
|
|
|
|
0 |
0 |
0 |
|||||||
Динаміка твердого тіла
Механічною системою матеріальних точок або тіл називаютьсѐ така їх сукупність, в ѐкій положеннѐ та рух кожної точки (або тіла) залежить від положеннѐ та руху решти.
Матеріальне тіло розглѐдаютьсѐ, ѐк система матеріальних точок (часток), ѐкі утворяять це тіло.
Класифікація сил, діючих на механічну систему.
e
Зовнішніми F n називаять такі сили, ѐкі діять на точки або тіла механічної системи з боку точок або тіл, ѐкі не належать даній системі.
i
Внутрішніми F n , називаять такі сили, ѐкі діять на точки або тіла механічної системи з боку точок або тіл тіюї ж системи, тобто з ѐкими точки або тіла даної системи взаюмодіять між собоя.
Зовнішні та внутрішні сили системи, в своя чергу можуть бути активними та реактивними.

Властивості внутрішніх сил.
1) Геометрична сума (головний вектор) всіх внутрішніх сил системи дорівняю нуля
k
Fni 0
n 1
2)Сума моментів (головний вектор) всіх внутрішніх сил системи відносно будь – ѐкого центра або осі дорівняю нуля
k
M O (Fni ) 0
n 1
Маса системи. Центр мас.
Маса системи дорівняю алгебраїчній сумі мас всіх точок або тіл системи
k
M mn ,
n 1
де М – маса механічної системи,
mn - маса n - точки системи.
В однорідному полі тѐжіннѐ, длѐ ѐкого g const , вага будь – ѐкої частки тіла пропорційна її масі. Тому розподіл мас у тілі можна визначити за положеннѐм його центра ваги – геометричної точки С( X C ,YC , ZC ), координати ѐкої визначаять за формулами (1.45), та називаять центром мас
або центром інерції механічної системи:
|
|
|
|
|
k |
|
|
|
|
k |
|
|
||
|
|
|
|
mn g xn |
|
|
|
|
mn xn |
|
|
|||
X |
|
|
|
n 1 |
|
|
|
n 1 |
, |
|||||
c |
|
m g |
|
m |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
k |
|
|
|
|
k |
|
|
||
|
|
|
mn g yn |
|
|
mn yn |
|
|
||||||
Y |
n 1 |
|
|
|
n 1 |
|
, |
|||||||
|
|
|
|
|||||||||||
c |
|
|
|
m g |
|
|
|
|
m |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
k |
|
|
|
|
k |
|
|
||
|
|
|
|
|
mn g zn |
|
|
|
|
mn zn |
|
|
||
Z |
|
|
n 1 |
|
|
n 1 |
|
|
||||||
c |
m g |
|
m |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||

Положеннѐ центра мас може визначити його радіус – вектором rC :
k
mn rn
|
|
|
r |
|
n 1 |
|
, |
|
|
|
|
|
|||
|
|
|
C |
m |
|||
|
|
|
|
|
|
||
|
|
|
|
|
|||
де rn - радіус – вектор кожної точки системи. |
|
|
|||||
Диференційні рівняння руху механічної системи.
Система n - матеріальних точок М1, М2,..М n , маса кожної точки відповідно mn , знаходитьсѐ
|
|
e |
|
i |
|
|
|
||
під діюя прикладених до точок зовнішніх та внутрішніх сил. Рівнодійні сил відповідно F n і |
F n . |
|||
Основне рівняння динаміки для кожної точки |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 r |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ma |
|
m |
|
|
|
|
|
|
|
|
|
n |
F e F i |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n dt 2 |
|
n |
n |
||||||||||||||||||
Длѐ механічної системи n - матеріальних точок буде отримано |
n - диференційних рівнянь руху |
||||||||||||||||||||||||||||||||
системи у векторному вигляді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
2 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
m a m |
|
|
|
F e |
|
F i |
|
|
|||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
dt 2 |
|
|
|||||||||||||||||||||||||||||
|
1 1 |
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
d |
2 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
m |
|
|
|
|
F e F i |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
m |
|
a |
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
dt 2 |
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|||||||||||||||||
|
|
.................................... |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
d |
2 r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
m |
|
|
|
|
F e F i |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
m |
|
a |
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
dt 2 |
|
|
|
|
||||||||||||||||||||||||
|
n |
|
|
n |
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|||||||||||
Загальні теореми динаміки
Теорема про рух центру мас механічної системи.
Теорема: центр мас механічної системи рухаютьсѐ ѐк матеріальна точка, маса ѐкої дорівняю масі системи, до ѐкої прикладені всі зовнішні сили, ѐкі діять на систему.
Висновки:
Механічну систему або тверде тіло можна розглѐдати ѐк матеріальну точку в залежності від характеру її руху, а не від її розмірів.
Внутрішні сили не враховуятьсѐ теоремоя про рух центру мас.

Теорема про рух центру мас не характеризую обертальний рух механічної системи, а тільки поступальний
Теорема про зміну кількості руху.
Кількість руху матеріальної точки – векторна величина (m V ) , ѐка дорівняю добутку маси
точки на вектор її швидкості.
Одиницея виміряваннѐ кількості руху ю (кг м/с).
Кількість руху механічної системи – векторна величина K , що дорівняю геометричній сумі (головному вектору) кількостей руху всіх точок системи.
k
Q mn Vn
n 1
або кількість руху системи дорівняю добутку маси всіюї системи на швидкість її центру мас
Q M VC
Коли тіло (або система) рухаютьсѐ так, що її центр мас нерухомий VC 0 , то кількість руху тіла дорівняю нуля Q 0 (приклад, обертаннѐ тіла навколо нерухомої осі, що проходить через центр мас тіла).
Якщо рух тіла складний, то Q не буде характеризувати обертальну частину руху при обертанні навколо центру мас. Тобто, кількість руху Q характеризує тільки поступальний рух системи (разом з центром мас).
Імпульс сили характеризую дія сили за деѐкий проміжок часу.
Імпульс S сили F за кінцевий проміжок часу t1 визначаютьсѐ ѐк інтегральна сума відповідних елементарних імпульсів
t1
S F dt
0
Проекції імпульсу сили на осі координат:
t1 |
t1 |
t1 |
S X FX dt , |
SY FY dt , |
SZ FZ dt |
0 |
0 |
0 |
Одиницея виміряваннѐ імпульсу сили ю ( кг м ).
с
Теорема про зміну кількості руху матеріальної точки
(в диференціальній формі):
Похідна за часом від кількості руху матеріальної точки дорівняю геометричній сумі діячих на точки сил.
|
|
|
k |
||
d (mV ) |
|||||
|
Fn |
||||
dt |
|||||
n1 |
|||||
Теорема про зміну кількості руху матеріальної точки
(в інтегральній формі):
Зміна кількості руху матеріальної точки за деѐкий проміжок часу дорівняю геометричній сумі імпульсів сил, прикладених до точки за той же проміжок часу.
k
mV1 mV0 Sn
n1
Теорема про зміну кількості руху механічної системи
(в диференціальній формі):
Похідна за часом від кількості руху системи дорівняю геометричній сумі всіх діячих на систему зовнішніх сил.
dQ k F e n dt n1
Теорема про зміну кількості руху механічної системи
(в інтегральній формі):
Зміна кількості руху системи за деѐкий проміжок часу дорівняю геометричній сумі імпульсів, діячих на систему зовнішніх сил, за той же проміжок часу.
k
Q1 Q0 S e n
n1
Закон збереження кількості руху системи.
1.Якщо сума всіх зовнішніх сил, діячих на систему, дорівняю нуля, то вектор кількості руху системи буде постійним за напрѐмком та за модулем.
2.Якщо сума проекцій всіх діячих зовнішніх сил на будь – ѐка довільну вісь дорівняю нуля, то проекціѐ кількості руху на ця вісь ю величиноя постійноя.
Закони збереженнѐ свідчать, що внутрішні сили не можуть змінити сумарну кількість руху системи.
