
Вишка. Клочко
.pdf
З цих двох теорем випливає такий наслідок.
Наслідок. Для того щоб два вектори були лінійно незалежними, необхідно і достатньо, щоб вони були неколінеарними.
Отже, всякі два колінеарні вектори є лінійно залежними, а всякі два неколінеарні вектори є лінійно незалежними.
Справедлива теорема.
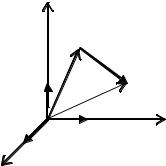
Теорема 3. (про розкладання вектора за двома неколінеарними векторами). Якщо вектори е1 і е2 неколінеарні, то будь-який компланарний з ними вектор а єдиним способом може бути розкладений за векторами е1
і е2.
Доведення. Нехай вектори е1 і е2 неколінеарні і нехай задано довільний вектор а, компланарний з ними. Приведемо всі ці три вектори е1, е2 і а до спільного початку. Спільну точку прикладання цих векторів позначимо через О, тоді згідно з означенням компланарних векторів, всі ці три вектори будуть розташовані в одній площині. Через кінець вектора а точку А проведемо прямі, паралельні з векторами е1 і е2, до перетину з прямими, на яких знаходяться відповідні вектори е1 і е2. Точки перетину, які існуватимуть, бо е1 і е2 неколінеарні, позначимо відповідно А1 і А2.
|
|
|
|
|
|
|
|
→ |
→ |
|
|
Фігура ОА1А А2 – паралелограм. Розглянемо вектори ОА1 і |
ОА2 , які є |
||||||||
|
|
|
|
сторонами |
паралелограма. |
Тоді |
за |
правилом |
||
|
|
|
|
|
|
|
→ |
дорівнюватиме сумі |
||
|
|
|
|
|
|
|
||||
|
|
|
|
паралелограма вектор а= ОА |
||||||
|
|
|
|
→ |
→ |
→ |
→ |
|
||
|
|
|
|
векторівОА1 і |
ОА2 |
, тобто а=ОА1 + |
ОА2 . |
|
||
|
|
|
|
→ |
|| е1, тоді існує цілком певне число |
|||||
|
|
|
|
|||||||
|
|
|
|
Але ОА1 |
||||||
|
|
|
|
α1 таке, |
що |
→ |
|
за теоремою про |
||
|
|
|
|
ОА1 = α1е1 |
||||||
|
|
|
|
|
|
|
→ |
|
|
|
колінеарні вектори. Аналогічно, оскільки вектори ОА2 і е2 |
колінеарні, то |
|||||||||
|
|
|
|
|
→ |
|
|
|
|
|
існує певне число α2 таке, що |
ОА2 = |
α2е2. Тоді |
попередня рівність |
|||||||
запишеться так: |
|
|
|
|
|
|
||||
|
|
|
|
а = α1е1 + α2е2, |
|
|
|
(2.8) |
||
тобто вектор а розкладено за векторами е1 і е2 і це розкладання єдине, бо точки А1 і А2 визначаються однозначно і відповідні числа α1 і α2 визначаються однозначно. Теорему доведено.
З цієї теореми випливає таке твердження.
Наслідок 2. Всякі три вектори на площині або всякі три компланарні вектори є лінійно залежні.
Дійсно, з рівності а = α1е1 + α2е2 випливає, що α1е1 + α2е2 – а = 0. Оскільки α3 = –1, тобто α3 ≠ 0, то за означенням випливає, що три вектори
е1, е2 і а є лінійно залежними. Справедлива і обернена теорема.
Теорема 4. Якщо три ненульові вектори лінійно залежні, то вони компланарні. Доводиться ця теорема аналогічно теоремі 2 з врахування
30
того, що сума двох векторів є вектор, що лежить в площині, утвореній векторами-доданками.
З цієї теореми і попереднього наслідку випливає такий наслідок.
Наслідок 3. Для того щоб три ненульові вектори були лінійно незалежними, необхідно і достатньо, щоб вони були некомпланарними.
І нарешті справедлива така теорема.
Теорема 5. Якщо три вектори е1, е2 і е3 некомпланарні, то будь-який вектор а єдиним способом може бути розкладений за цією трійкою
векторів е1, е2 і е3.
Доведення. Зауважимо, що якщо три вектори є некомпланарними, то будь-яка пара цих векторів не є колінеарними, бо в протилежному випадку ця трійка векторів була б компланарною, що очевидно, якщо ці вектори привести до спільного початку.
Зведемо всі ці чотири вектори е1, е2, е3 і а до спільної точки прикладання О. Два неколінеарні вектори е1 і е2 утворять площину, що
натягнута |
на них. Через |
кінець |
вектора а точку |
А проведемо пряму |
||||||
|
|
|
А |
паралельно вектору е3 до перетину з площиною, |
||||||
|
|
а |
утвореною |
векторами е1 і |
е2. |
Точку перетину цієї |
||||
е3 |
|
|
прямої з площиною позначимо М, зауважимо, що ця |
|||||||
|
|
|
||||||||
е2 |
|
точка єдина. За означенням суми векторів матимемо, |
||||||||
О |
|
|
→ |
→ |
→ |
|
→ |
|||
|
М |
|
що а =ОА |
=ОМ + МА . Але вектор МА колінеарний |
||||||
|
е |
|
вектору е3, |
тоді за теоремою про колінеарні вектори |
||||||
|
1 |
|
|
|
|
|
→ |
|
|
|
Рисунок 2.8 |
матимемо, що МА = α3е3, де α3 – цілком певне число. |
|||||||||
Вектор |
→ |
що |
лежить |
в |
площині, утвореній |
|||||
|
|
|
|
ОМ , |
||||||
неколінеарними векторами е1 і е2, на підставі теореми 3 єдиним способом
може бути розкладений за векторами е1 і е2, тобто |
→ |
+ α2е2, де α1 і |
ОМ = α1е1 |
||
α2 – певні числа. Тоді попередня рівність буде записана так: |
|
|
а = α1е1 + α2е2 + α3е3, |
|
(2.9) |
тобто вектор а єдиним способом розкладено за даними некомпланарними векторами е1, е2 і е3. Теорему доведено.
Зауважимо, що з рівності а=α1е1+α2е2+α3е3 випливає, що α1е1+α2е2+ +α3е3–а=0. Оскільки α4= –1, тобто α4≠0, то четвірка векторів е1, е2, е3 і а є
лінійно залежними.
Отже, доведено таку теорему.
Теорема 6. Всякі чотири вектори в просторі є лінійно залежними.
Ось таке твердження має місце в реальному просторі.
2.5 Поняття базису та координат вектора
Поняття базису є дуже важливим у векторній алгебрі. Щоб щось назвати базисом, треба від нього вимагати певної якості: міцності, як у будівництві, незалежності, як в побуті і суспільстві, лінійної незалежності,
31
як у векторній алгебрі.
Означення. Кажуть, що упорядкована трійка лінійно незалежних
векторів е1, е2, е3 утворює базис у просторі, якщо будь-який вектор а простору можна подати у вигляді деякої лінійної комбінації векторів е1, е2
і е3.
Означення. Кажуть, що упорядкована пара лінійно незалежних
векторів е1 і е2 утворює базис на площині, якщо будь-який вектор а площини можна подати у вигляді деякої лінійної комбінації векторів е1 і е2.
З наслідку 1 і наслідку 3 та на підставі теореми 3 і теореми 5
випливає, що будь-яка відповідно пара неколінеарних або будь-яка трійка некомпланарних векторів утворює відповідно базис на площині або базис в просторі.
Нехай неколінеарні вектори е1 і е2 утворюють базисна площині, тоді на підставі теореми 3 будь-який вектор а цієї площини єдиним способом може бути розкладений за базисними векторами е1 і е2 або може бути поданий у вигляді(2.8), а саме:
а = α1е1 + α2е2,
де α1 і α2 визначаються однозначно. Ці коефіцієнти лінійної комбінації (2.8) називаються координатами вектора а відносно базису {е1, е2}.
Отже, будь-якому вектору а у заданому базисі на площині {е1, е2} однозначно відповідає пара чисел α1 і α2, які називаються координатами вектора а відносно базису {е1, е2}, і це символічно записується так: а = (α1, α2), або а = {α1, α2}, або а{α1, α2}, що читається так: вектор а – це вектор з координатами α1 і α2 або вектор а дорівнює вектору, координатами якого є числа α1 і α2. І навпаки, кожній упорядкованій парі чисел (α1, α2) відносно базису {е1, е2} можна поставити у відповідність певний вектор а.
Якщо ж три некомпланарні вектори е1, е2 і е3 утворюють базис у просторі, то на підставі теореми 5 будь-який вектор а простору єдиним способом можна розкласти за цими базисними векторами або може бути поданим у вигляді рівності (2.9), тобто
а = α1е1 + α2е2 + α3е3,
де числа α1, α2 і α3 визначаються однозначно. Ці числа називаються
координатами вектора а відносно базису{е1, е2, е3}. І навпаки, кожній упорядкованій трійці чисел (α1, α2, α3) відносно базису {е1, е2, е3} однозначно ставиться у відповідність певний вектор а, що символічно
записують так: а = (α1, α2, α3), або а = {α1, α2, α3}, або а{α1, α2, α3}.
Отже, якщо введено базис на площині або в просторі, то будь-якому вектору а відносно базису ставиться у відповідність упорядкована пара або трійка чисел, що називаються координатами цього вектора (без базису немає координат вектора).
Головне значення введення поняття базису полягає в тому, що всякому вектору відповідає упорядкована пара або трійка чисел, тобто вектор описується числами, які називаються координатами цього вектора,
32
а лінійні операції над векторами виконуються як відповідні операції над звичайними числами (парами або трійками чисел), що буде показано в наступному пункті.
2.6 Лінійні операції над векторами, що задані координатами
Вияснимо, як виконуються операції додавання, віднімання векторів і множення вектора на число, якщо вектори задані своїми координатами відносно вибраного базису. Справедливі такі дві теореми.
Теорема 1. При додаванні (відніманні) векторів додаються (віднімаються) їх відповідні координати.
Доведення. Нехай в просторі вибрано певний базис {е1, е2, е3} і розглядаються два вектори а і b, задані своїми координатами відносно
цього базису, а саме: а = α1е1 + α2е2 + α3е3 і b = β1е1 + β2е2 + β3е3. Тоді на підставі властивоcтей операції додавання векторів і множення вектора на
число (переставний, сполучний і розподільний закони) будемо мати:
а + b = (α1е1 + α2е2 + α3е3) + (β1е1 + β2е2 + β3е3) = (α1е1 + β1е1) + (α2е2 + β2е2) +
+ (α3е3 + β3е3) = (α1+β1)е1 + (α2 +β2)е2 + (α3+β3)е3. Отже, а + b = (α1+β1)е1 + (α2+β2)е2 + (α3+β3)е3 або
а + b = ( α1+β1; α2+β2; α3+β3) відносно базису {е1, е2, е3}.
Теорема 2. При множенні вектора на число всі його координати множаться на це число.
Доведення. Нехай задано вектор а = α1е1 + α2е2 + α3е3 відносно базису {е1, е2, е3}, тоді добуток цього вектора на деяке число λ, користуючись властивостями цієї дії (розподільний та сполучний закони), визначимо так:
λа = λ(α1е1 + α2е2 + α3е3) = λ(α1е1) + λ(α2е2) + λ(α3е3) = (λα1)е1 + (λα2)е2+ (λα3)е3
або λ а = (λα1; λα2; λα3), що і треба було довести.
Наслідок. Якщо два вектори колінеарні, то їх координати пропорційні і навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.
Дійсно, нехай відносно деякого базису {е1, е2, е3} задано два
колінеарні вектори: а=α1е1+α2е2+α3е3 і b=β1е1+β2е2+β3е3. За теоремою про колінеарні вектори випливає, що b = λа, де λ – деяке число. На підставі
теореми 2 матимемо, що λа = (λα1; λα2; λα3) відносно базису {е1, е2, е3}. З рівності b=λа випливає, що в рівних векторів рівні їх відповідні координати, тобто β1 = λα1, β2 = λα2, β3 = λα3. Виключивши з кожної
рівності λ, будемо мати: λ = |
β1 |
, λ = |
β2 |
, λ = |
β3 |
, звідки |
β1 |
= |
β2 |
= |
β3 |
. |
||||
α |
|
|
α |
|
|
|||||||||||
|
|
α |
2 |
|
α |
3 |
|
|
α |
2 |
|
α |
3 |
|
||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||
Зауваження. Важливим на практиці є випадок, коли базисні вектори взаємно перпендикулярні і одиничні. Такий базис в просторі називається декартовим. Базисні вектори декартового базису позначаються так: i, j, k.
Отже, | i | = | j | = | k | = 1 і i j, i k, j k. Рене Декарт (1596–1650) –
французький математик і філософ вважається основоположником сучасного наукового мислення. Єдина його книга з математики Геометрія”
33

була опублікована в 1635 році. Декартів базис узгоджують з прямокутною |
|||||||
системою координат в просторі Охуz таким чином: спільну точку їх |
|||||||
прикладання розміщують в початку координат прямокутної системи. Орт i |
|||||||
збігається з координатною віссю Ох, орт j збігається з віссю Оу, а орт k |
|||||||
збігається з віссю Оz. |
|
|
|
|
|
|
|
2.7 Проекція вектора на вісь |
|
|
|
|
|||
Нагадаємо поняття числової осі. |
|
|
|
|
|||
Означення. Числовою віссю називається пряма, на якій вибрано |
|||||||
початкову точку О, вказано додатний напрям та одиничний відрізок, так |
|||||||
звану одиницю масштабу. |
|
|
|
→ |
|
||
|
|
|
|
|
|
|
|
Нехай l – деяка числова вісь і задано деякий вектор АВ = а. Через А' i |
|||||||
|
B' |
позначимо проекції на цю вісь початкової точки А і |
|||||
|
кінцевої точки В вектора а, які є точками перетину з |
||||||
|
віссю |
l площин, що |
|
проходять через точки А і В |
|||
|
перпендикулярно осі l. Нехай х1 –координата точки |
||||||
ϕ |
А' , |
а х2 – координата точки |
B' , які лежать на самій |
||||
|
осі. Розглянемо число х2 – х1, його і назвемо проекцією |
||||||
|
вектора а на вісь l. |
|
|
|
|
||
|
|
Означення. Різниця х2 – х1 між координатами |
|||||
|
проекцій на вісь l кінця і початку вектора а |
||||||
називається проекцією вектора а на вісь l і позначають символом прl а |
|||||||
→ |
|
|
|
|
|
|
|
або прl АВ . |
|
|
прl а = х2 – х1. |
|
|
|
|
Отже, |
|
|
|
|
|
(2.10) |
|
Зауваження. Якщо через φ позначити величину кута між вектором а |
|||||||
і віссю l, то дістанемо рівність |
|
|
|
|
|||
|
прl а = |а| соs φ. |
|
|
|
(2.11) |
||
Це видно з рис. 2.9, якщо провести пряму А'С паралельно прямій АВ, де С |
|||||||
|
|
|
– точка перетину А'С з прямою ВВ' . Оскільки |
||||
|
|
|
трикутник А'В'С – |
прямокутний (Ð В' =90º, |
|||
|
|
|
Ð B' A'С =φ), |
то |
А' В' / А'С =соsφ, |
звідки |
|
|
|
|
А' В' = А'С соsφ. Але А'С =|а|, тоді А' В' =|а|соsφ, |
||||
|
|
|
тобто прl а = |а| соs φ. |
|
|
||
|
|
|
Якщо кут φ – гострий, то соs φ > 0 і прl а є |
||||
|
|
|
число додатне, |
що |
узгоджується з тим, що |
||
|
|
|
х2 – х1> 0; якщо ж кут φ – тупий, то соs φ < 0 і |
||||
|
|
|
прl а є число від’ємне, що відповідає тому, що |
||||
|
|
|
х2 – х1< 0, бо х2< х1. |
тлумачення декартових |
|||
|
|
|
Дамо геометричне |
||||
|
|
|
координат вектора. Нехай вектор а зада- |
||||
но координатами в декартовому базисі {i; j; k}, які будемо позначати Х, У, |
|||||||
|
|
|
34 |
|
|
|
|

Z, тобто а = Хi + Уj + Zk |
або а = (Х, У, Z). Справедлива така теорема. |
|
Теорема 4 |
(про |
декартові координати вектора). Декартові |
координати Х, У, |
Z вектора а дорівнюють проекціям цього вектора на |
|
координатні осі Ох, Оу і Оz, що визначаються відповідно ортами i, j, k.
Доведення. Нехай вектор а заданий своїми декартовими координатами Х, У, Z, тобто а=Хi+Уj+Zk. Приведемо декартів базис {i; j; k} до спільної точки прикладання, яку позначимо О. Цю точку будемо вважати початком координат прямокутної декартової системи координат, при цьому вісь Ох виберемо так, щоб вона збігалась з першим ортом i, осі Оу і Оz виберемо так, щоб вони збігалися відповідно з ортами j і k. Початок вектора а
→
помістимо теж в точку О і побудуємо вектор ОМ = а. Спроектуємо кінець вектора а точку М на координатні осі, позначивши їх відповідно А, В і С, спроектувавши спочатку точку М на координатну площину хОу і
позначивши цю проекцію буквою М' , |
а вже потім проектуємо точку М' |
||||||||
на осі Ох і Оу. Розглянемо вектори |
→ |
→ |
і |
→ |
що |
лежать |
на |
||
ОА , |
ОВ |
ОС , |
|||||||
координатних |
осях. Тоді, |
|
→ |
→ |
→ |
|
→ |
→ |
→ |
оскільки ОМ =ОМ ′+ОС , а |
ОМ |
′=ОА +ОВ |
|||||||
(за правилом |
паралелограма), матимемо, |
що |
|
→ |
→ |
→ |
→ |
||
а=ОМ =ОА +ОВ +ОС . |
|||||||||
|
→ |
лежать на |
одній |
прямій, |
то |
→ |
(прОх |
а)·і. |
|
Оскільки вектори ОА і і |
ОА = |
||||||||
→ |
|
→ |
|
|
|
|
|
|
|
Аналогічно ОВ = (прОу а)·j і |
ОС = (прОz а)·k. |
|
|
|
|
|
|
||
Отже, а = (прОх а)·і + (прОу а)·j + (прОz а)·k.
З другої сторони а = Хi + Уj + Zk (за умовою). Звідси будемо мати, що
Х = прОх а, У = прОу а, Z = прОz а. |
(2.12) |
Введемо важливі поняття напрямних косинусів вектора. |
|
Позначимо грецькими буквами α, β і γ кути нахилу вектора а до |
|
додатних напрямів координатних осей Ох, Оу і Оz.
Числа cosα, cosβ, cosγ називаються напрямними косинусами вектора а.
Враховуючи ці позначення і користуючись формулою (2.11), формули (2.12) можна записати так:
Х =|а| cosα, У =|а| cosβ, Z =|а| cosγ. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Неважко бачити, що |а| = |
|
|
Х 2 +У 2 + Z2 . |
|
|
(2.13) |
||||||||||
Дійсно, |
|ОМ |2=|ОМ' |2+|ОС |2 і |ОМ' |2=|ОА |2+|ОВ|2 (за властивістю |
|||||||||||||||
діагоналей |
|
прямокутника). |
|
|
Тоді |
|ОМ |2=|ОА |2+|ОВ|2+|ОС |2 |
або |
|||||||||
|а|2=Х2+У2+Z2. |
|
|
|
Х |
|
|
|
|
|
У |
|
|
|
|||
Тоді cosα = |
|
|
|
, cosβ = |
|
|
|
, |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
Х 2 + У 2 + Z2 |
Х 2 + У 2 + Z2 |
|
||||||||||||||
|
|
|
Ζ |
|
|
|
|
|
|
|
|
|
||||
cosγ = |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
(2.14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Х 2 + У 2 + Z2 |
|
|
|
|
|
|
|
|
|
|||||
35
Звідси дістанемо, що cos2α + cos2β + cos2γ = 1. |
(2.15) |
Нарешті відзначимо ще деякі властивості проекції вектора на вісь, а саме:
−якщо вектор перпендикулярний до осі, то його проекція на цю вісь дорівнює нулю. Це очевидно, бо cos π2 = 0.
−проекція суми векторів на вісь дорівнює сумі проекцій цих векторів на цю вісь.
−проекція на вісь добутку вектора на число дорівнює добутку цього числа на проекцію вектора на цю вісь.
Доведення. Нехай вектори а і b задані своїми декартовими
координатами, а саме а = Х1i + У1j + Z1k і b = Х2i + У2j + Z2k. Припустимо, що прямокутна система координат вибрана так, щоб вісь Ох збіглася з
даною віссю l.
Оскільки а + b = (Х1 + Х2)i + (У1 + У2)j + (Z1 + Z2)k і λа = λХ1i +λУ1j + +λZ1k, то, враховуючи геометричний зміст декартових координат
відповідних векторів, а саме Х1 = прОх а = прl а, Х2 = прОхb = прlb, і Х1 + Х2 =
= прОх(а + b) = прl(а + b) і λХ1 = прОх (λа) = прl(λа), будемо мати, що |
|
прl(а + b) = прlа + прl b, |
(2.16) |
прl(λа) = λ прlа. |
(2.17) |
Обидві властивості доведено. |
|
2.8 Задання вектора координатами його початку і кінця
Звернемо увагу на те, що вектор повністю визначається заданням його початку А і кінця В.
Нехай у вибраній декартовій системі координат Охуz задані координати точок А(х1, у1, z1) і В(х2, у2, z2). Треба визначити координати
вектора |
→ |
|
|
→ |
→ |
|
|
|
||
АВ . |
Розглянемо вектори ОА і |
ОВ , які називаються радіусами- |
||||||||
|
z |
|
|
векторами точок А і В. |
|
|
|
|||
|
|
|
|
Означення. Вектор, що з’єднує початок |
||||||
|
|
А |
|
|
||||||
|
r1 |
|
координат з точкою М простору, називається |
|||||||
|
k |
|
радіусом-вектором |
точки |
М позначається |
|||||
|
|
r2 |
В |
|
|
|
→ |
|
|
|
|
|
символом r, тобто r = ОМ . |
|
|
|
|||||
|
|
|
|
|
||||||
|
|
|
у |
Позначимо радіуси-вектори точок А і В через r1 і |
||||||
|
|
|
||||||||
і |
j |
|
||||||||
|
|
→ |
, r2 |
→ |
|
|
|
|||
x Рисунок 2.11 |
r2, тобто r1 = ОА |
= ОВ . |
|
|
|
|||||
|
Визначимо координати цих радіусів-векторів. |
|||||||||
|
|
|
|
|
||||||
Очевидно, що |
проекції |
радіуса-вектора |
→ |
на |
координатні |
осі |
||||
ОМ |
||||||||||
дорівнюють координатам точки М. Тоді координати радіуса-вектора |
→ |
|||||||||
ОМ |
||||||||||
дорівнюють координатам точки М. |
|
|
|
|
|
|||||
|
Отже, r1 = х1і+у1j+z1k, |
r2=х2і + у2j + z2k. |
|
|
|
|
||||
36
|
→ |
→ → |
→ |
– r1, то матимемо |
|
Оскільки вектор АВ = |
ОВ –ОА , тобто АВ = r2 |
||
|
→ |
|
|
(2.18) |
|
АВ = (х2 – х1)і + (у2– у1)j + (z2 – z1)k |
|||
або |
→ |
|
– z1). |
|
АВ = (х2 – х1; у2– у1; z2 |
|
|||
Отже, декартові координати вектора, що задається координатами початкової і кінцевої його точки, дорівнюють різницям однойменних координат його кінця і початку.
Приклад 1. |
→ |
Знайти координати вектора АВ , якщо А(1; –2; 3), |
|
В(2;1;–1). |
|
Розв’язування. Користуючись формулою (2.18), маємо |
|
→ |
→ |
АВ = (2–1; 1–(–2); –1–3) або АВ = (1; 3; – 4).
Відповідь: (1; 3; – 4).
2.9 Поділ відрізка в даному відношенні
Нехай точки А і В задані своїми декартовими координатами, а саме: А(х1, у1, z1) і В(х2, у2, z2) і задано відношення λ, в якому точка С поділяє
напрямлений відрізок АВ, тобто СВАС = λ . Треба знайти координати точки
С, що ділить відрізок АВ в даному відношенні λ.
Позначимо координати точки С через х, у, z. З’єднаємо точки А, В і С, що лежать на одній прямій з початком координат О, і розглянемо радіуси-вектори цих точок, а
|
→ |
|
|
|
→ |
→ |
→ |
|
саме: r1 = ОА , r2 |
= ОВ і r = ОС . Оскільки |
АС = |
||||||
|
→ |
|
|
|
|
→ |
→ |
|
=r – r1, СВ = r2 |
– r, то враховуючи те, що АС |
і СВ |
||||||
колінеарні і |
|
АС |
|
= λ , на підставі теореми |
про |
|||
СВ |
||||||||
|
|
|
|
|
||||
колінеарні вектори будемо мати: |
|
|||||||
→ |
→ |
|
|
|
= λ(r2 – r). |
(2.19) |
||
АС =λ |
СВ або r–r1 |
|||||||
Оскільки |
|
в |
рівних |
векторів рівні їх |
||||
кординати, то будемо мати: х–х1=λ(х2 – х); у– у1= λ(у2– у), z – z1= λ (z2 – z). Звідки маємо:
х = |
х1 + λx2 |
; у = |
у1 + λy2 |
; z = |
z1 + λz2 |
. |
(2.20) |
1+ λ |
1+ λ |
|
|||||
|
|
|
1+ λ |
|
|||
Зауваження. Якщо точка С – середина напрямленого відрізка АВ, то λ = 1, бо АС = СВ, тоді з формул (2.20) дістанемо формули координат середини відрізка:
х = |
х1 + х2 |
; у = |
у1 + у2 |
; z = |
z1 + z2 |
. |
(2.21) |
|
|
||||||||
2 |
2 |
2 |
||||||
|
|
|
|
|
37
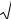
2.10 Скалярний добуток векторів
Для дії множення векторів вводяться кілька видів добутків векторів, а саме: скалярний добуток, векторний добуток, мішаний добуток, подвійний векторний добуток тощо.
Розглянемо спочатку поняття скалярного добутку векторів.
Означення. Скалярним добутком двох векторів називається число,
що дорівнює добутку модулів цих векторів на косинус кута між ними.
Скалярний добуток двох векторів а і b позначається символом а · b
→ →
або ( а , b ), або (а , b).
Отже, за означенням скалярного добутку маємо: |
|
а · b = | а |·| b | cоsφ, |
(2.22) |
де φ – кут між векторами а і b або φ = (а ,^ b).
Такий вид множення двох векторів використовується у фізиці та інших навчальних дисциплінах. Така операція використовується в механіці при визначенні роботи, що виконується сталою силою F при переміщенні точки прикладання сили на деякий вектор переміщення S. Як відомо, шукана робота А дорівнює чисельно добутку складової цієї сили на вектор переміщення FS, помноженій на модуль вектора переміщення, тобто А = FS·| s |. Оскільки FS = | F | cosφ, де φ – кут між вектором сили F і вектором переміщення s, то будемо мати: А=|F|·|s|cosφ або,
використовуючи формулу (2.22), матимемо: |
|
А = F · s. |
(2.23) |
Отже, робота сили F при переміщенні її точки |
прикладання на |
вектор переміщення s дорівнює чисельно скалярному добутку вектора сили на вектор переміщення. Такий фізичний зміст можна надати скалярному добутку двох векторів.
Відзначимо властивості скалярного добутку векторів.
10 . Скалярний добуток векторів підпорядкований переставному закону, а саме а · b = b · а, що очевидно.
20 . Якщо вектор а ненульовий, то а · а > 0. Якщо вектор а – нульовий, то а · а = 0.
Дійсно, оскільки а · а = | а |·| а | cos0 і оскільки cos0 = 1, то маємо, що
а · а = | а |2, звідки видно, що а · а > 0. |
|
|
|
|
А з рівності а·а = |а|2 випливає, що | a |= |
|
. |
(2.24) |
|
a ×a |
||||
Отже, модуль вектора |
дорівнює арифметичному кореню із |
|||
скалярного квадрата вектора. |
|
|
|
|
30 . Скалярний добуток двох векторів |
дорівнює |
модулю одного з |
||
векторів, помноженому на проекцію іншого вектора на напрям першого,
тобто
а · b = | а | пра b = | b | прb а. |
(2.25) |
Дійсно, за означенням, враховуючи формулу (2.11), маємо:
а b = | а |·| b |cоsφ = | а |·(| b |cоsφ) = | а |пра b і а b = | b |·| а |cоsφ = | b |прb а.
38

40 . Скалярний множник можна виносити за знак скалярного
добутку векторів, а саме: |
|
(αа)· b = α (а·b) і а·(βb) = β(а·b). |
(2.26) |
Дійсно, користуючись попередньою властивістю і властивістю проекції вектора на вісь, маємо, що:
→
(αа)· b =| b | прb (αа) = | b |·α·прb а = α(| b |·прb а) = α (а·b).
50 . Скалярний добуток підпорядкований розподільному закону, а саме:
а·(b + с) = а·b + а·с. |
(2.27) |
Дійсно, за властивістю 3˚ маємо а·(b + с) = | а |·пра (b + с) = | а |(пра b + + пра с) = | а |·пра b + | а |·пра с = а·b + а·с.
60 . Для того, щоб два ненульові вектори були перпендикулярні, необхідно і достатньо, щоб їх скалярний добуток дорівнював нулю.
Необхідність. Якщо а b, то а·b = | а |·| b |cоs π2 =| а |·| b |·0 = 0.
Достатність. Якщо а·b = 0, то ця рівність запишеться так:
| а |·| b |cоsφ = 0. Оскільки | а | ≠ 0 і | b | ≠ 0, то звідси випливає, що cоsφ = 0,
звідки φ = π2 , тобто вектори а і b перпендикулярні.
2.11 Вираження скалярного добутку векторів через їх декартові координати
Нехай вектори а і b задані своїми декартовими координатами
а = Х1i + У1j + Z1k і b = Х2i + У2j + Z2k.
Користуючись властивостями скалярного добутку (2˚, 4˚, 5˚ і 6˚) знайдемо їх скалярний добуток:
аb=(Х1i+У1j+Z1k)·(Х2i+У2j+Z2k)=Х1Х2(i·i)+Х1У2(i·j)+Х1Z2(i·k)+У1Х2(j·i)+
+У1У2(j·j)+У1Z2(j·k)+Z1Х2(k·i)+Z1У2(k·j)+Z1Z2(k·k)=Х1Х2(i·i)+У1У2(j·j)+Z1Z2× ×(k·k)=Х1Х2|і|2+У1У2| j|2+Z1Z2|k|2=Х1Х2·1+У1У·1+Z1Z2·1=Х1Х2 + У1У + Z1Z2.
Отже, |
а·b = Х1Х2 + У1У + Z1Z2. |
(2.28) |
Доведено таку теорему. |
|
|
Теорема. |
Скалярний добуток двох векторів, |
заданих своїми |
декартовими координатами, дорівнює сумі добутків їх відповідних координат.
Саме це твердження в шкільному курсі виступало як означення скалярного добутку векторів, що не зовсім правильно.
Наслідок 1. Користуючись формулами (2.28) і (2.24), легко дістанемо відому формулу для модуля вектора а = (Х; У; Z), заданого своїми
декартовими координатами: |
|
| а | = Х 2 +У 2 + Z2 . |
(2.29) |
39
