
- •1.1. Центральне проектування
- •1.2 Паралельне проектування
- •1.3 Ортогональне проектування
- •2. Комплексне креслення
- •2.1. Комплексне креслення точки
- •2.2. Комплексне креслення прямої
- •2.3. Комплексне креслення площини
- •1. Взаємне положення точок і прямих, їхня
- •1.2. Взаємне положення прямих
- •1.3. Приналежність точки й прямої площині
- •2. Перша і друга позиційні задачі
- •2.1. Взаємне положення прямої і площини
- •2.2.1. Площина займає проектуюче положення
- •2.2.2. Пряма займає проектуюче положення
- •2.3.1. Паралельні площини
- •2.3.2. Перетин площин
- •2.3.3. Побудова лінії перетину двох площин по точках перетину
- •1. Метричні задачі. Ортогональна проекція
- •3) Визначення кутів між фігурами.
- •2. Побудова взаємно перпендикулярних фігур
- •2.1 Перпендикулярність двох прямих
- •2.2. Перпендикулярність прямої і площини
- •2.3. Лінії найбільшого нахилу
- •2.4. Дотична площина й нормаль до поверхні
- •2.5. Перпендикулярність двох площин
- •1. Спосіб заміни площин проекцій
- •1.1. Визначення відстані між двома точками
- •2. Спосіб обертання
- •2.1. Застосування способу обертання без вказівки на кресленні осей
- •2.2.Спосіб обертання навколо прямих, паралельних площинам
- •2.3. Спосіб суміщення
- •1. Визначення відстаней
- •1.1. Відстань від точки до фігури (точки, прямої, площини)
- •1.2. Визначення відстані між паралельними фігурами
- •1.3. Визначення відстані між мимобіжними прямими
- •2. Визначення кутів між фігурами
- •2.1. Кути між прямими
- •2.2. Кут між прямою і площиною
- •2.3. Кут між площинами
- •2. Комплексне креслення кола
2. Спосіб обертання
Як відомо, при обертанні деякої точки навколо осі вона рухається в
площині, перпендикулярній до осі обертання, і описує коло. Для застосування
способу обертання з метою перетворення креслення відзначимо наступні
чотири елементи (рис. 4.9):
- вісь обертання (MN);
- площина обертання точки (пл. S
перпендикулярна (MN));
- центр обертання (O; пл. S
перетинає (MN)=О);
- радіус обертання (R ;R=|ОA|).
Яквісьобертаннязвичайно
використовуютьпрями,які
перпендикулярніабопаралельні
площинам проекцій. При обертанні
точки навколо вертикальної осі, її
горизонтальнапроекція
переміщується по колу, а фронтальна
проекція - паралельна осі X, тобто
перпендикулярна до осі обертання.
Обертання точки А на кресленні щодо осі MN, перпендикулярної до площини
П1 .
При обертанні точки навколо горизонтальної осі її фронтальна проекція
буде переміщуватися по колу , а горизонтальна - паралельно осі X .
48
 Обертання
точки А на кресленні відносно осі MN,
перпендикулярної
Обертання
точки А на кресленні відносно осі MN,
перпендикулярної
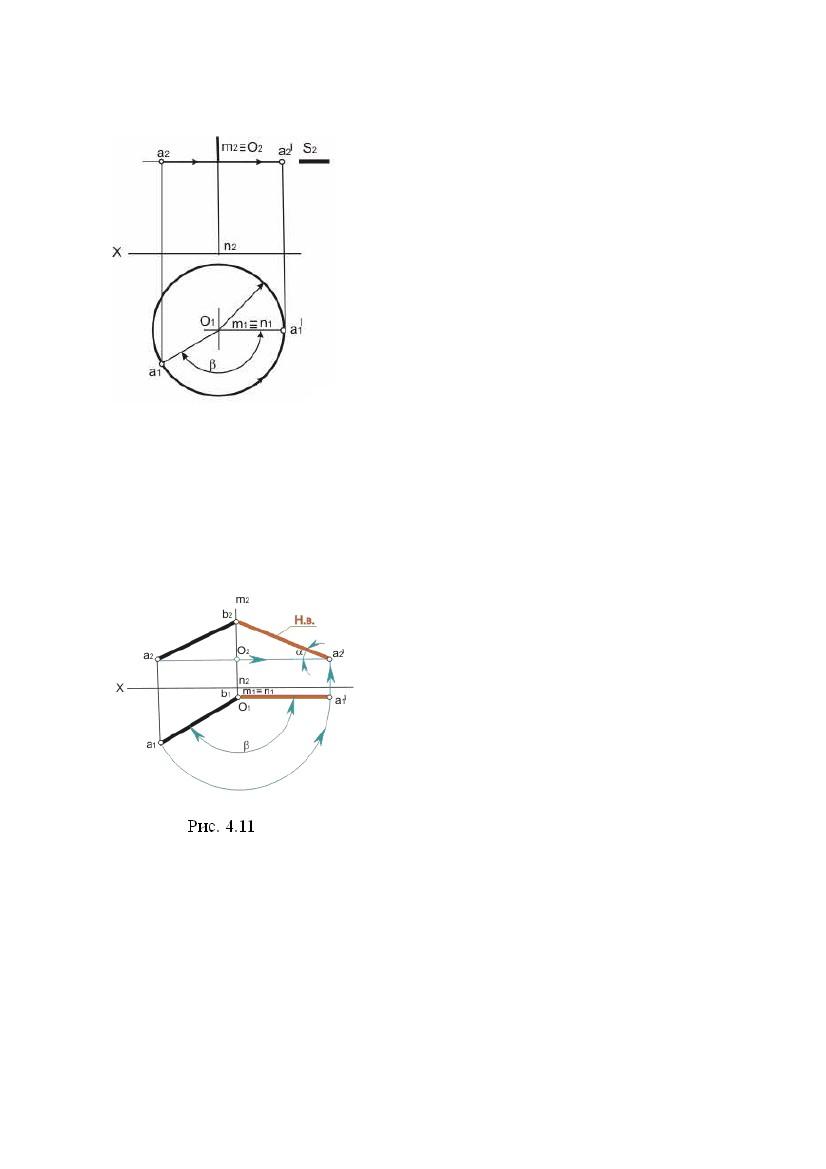
до площини П1, показане на рис. 4.10.
Площина обертання S2 паралельна площині П1
і на фронтальній проекції зображена слідом S2.
Горизонтальна проекція О1 центра обертання
O збігається із проекцією m1n1 осі, а
горизонтальнапроекціяО1a1радіуса
обертання ОА є його натуральною величиною.
Поворот точки А на рис. 4.10 зроблений на кут
β проти годинникової стрілки так, щоб у
новому положенні точки із проекціями a′2, a′1
радіус обертання був паралельний площині П2.
При обертанні точки навколо вертикальної осі
її горизонтальна проекція переміщується по
колу, а фронтальна проекція – паралельна осі
Рис. 4.10
X і перпендикулярна до осі обертання.
Якщо точку обертати навколо осі, перпендикулярної до площини П2, то її
фронтальна проекція буде переміщуватися по колу, а горизонтальна -
паралельно осі X.
Обертання точки навколо проектуючої прямої застосовують при
вирішенні деяких задач, наприклад при визначенні натуральної величини
відрізка прямої. Для цього (рис. 4.11) досить вісь обертання із проекціями m1n1,
m2n2 вибрати так , щоб вона проходила
через одну з крайніх точок відрізка,
наприклад точку із проекціями b2, b1.
Тоді при повороті точки А на кут β у
положення А′ (ОА′ || пл. П2, o1a′1 || осі Х)
відрізок АВ переміщується в положення
А′В, паралельне площині П2 і, отже,
проектується на неї в натуральну
величину. Одночасно в натуральну
величину буде проектуватися кут α
нахилу відрізка АВ до площини П1.
2.1. Застосування способу обертання без вказівки на кресленні осей
обертання, перпендикулярних до площин проекцій
Якщо обертати геометричну фігуру навколо осі, перпендикулярної до
площини проекцій, то проекція на цій площині не змінюється ні за видом, ні за
величиною (міняється лише положення проекції щодо осі проекцій). Проекції
точок геометричної фігури на площині, паралельній осі обертання,
переміщуються по прямих, паралельних осі проекції ( за винятком проекцій
49
 точок,
розташованих на осі обертання), і проекція
в цілому змінюється за
точок,
розташованих на осі обертання), і проекція
в цілому змінюється за
формою і величиною. Тому можна застосовувати спосіб обертання, не
задаючись зображенням осі обертання. У цьому випадку, не змінюючи
величини і форми однієї із проекцій геометричного образа, переміщують цю
проекцію в необхідне положення, а потім будують іншу проекцію так, як
зазначено вище.
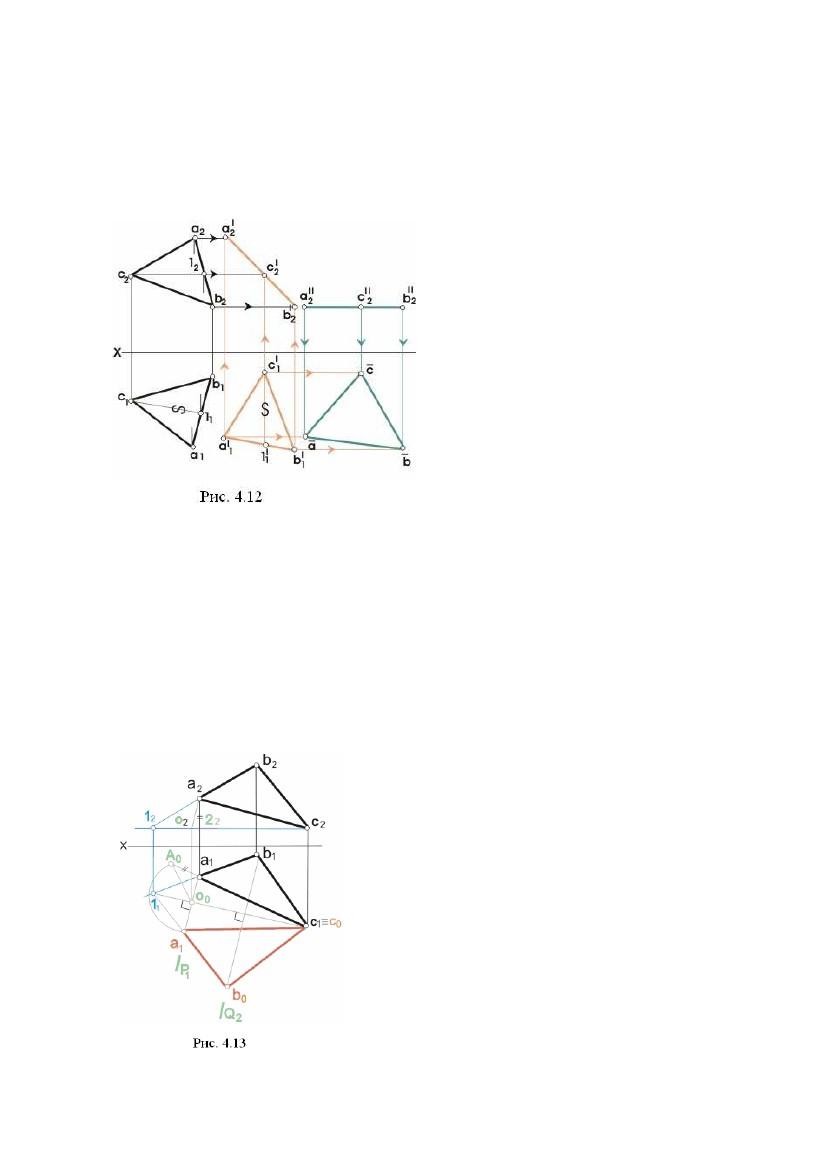
Нарис.4.12показане
застосування способу обертання
без вказівки осей для визначення
натуральної величини трикутника
АВС, заданого проекціями a1b1з1,
а2b2з2. Для цього виконано два
повороти площини загального
положення, в якій розташований
трикутник так, щоб після першого
повороту ця площина стала
перпендикулярною до площини
П2, а після другого - паралельна
площині П1.
Застосування способу обертання без вказівки осей трохи спрощує побудови,
при цьому не відбувається накладення однієї проекції на іншу, але креслення
займає більшу площу.
