
- •Кафедра высшей математики
- •Обыкновенные дифференциальные уравнения
- •Дифференциальные уравнения первого порядка. Общие понятия
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Уравнения с разделяющимися переменными
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Замена переменных в дифференциальных уравнениях первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Однородные уравнения
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные уравнения первого порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Смешанные задачи на дифференциальные уравнения первого порядка
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Дифференциальные уравнения высших порядков
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Линейные однородные дифференциальные уравнения n-го порядка
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные однородные уравнения с постоянными коэффициентами
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод неопределенных коэффициентов
- •Сведения из теории
- •И соответствующие им частные решения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Линейные неоднородные дифференциальные уравнения n-го порядка. Метод вариации произвольных постоянных
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Список литературы
- •5.3.9. А); б).
- •Вариант 1
- •150023, Ярославль, Московский пр., 88
Задачи для самостоятельного решения
Убедиться, что заданное семейство функций является общим решением дифференциального уравнения. Сделать рисунок интегральных кривых. Выделить интегральную кривую, проходящую через точку (1;1).
а)
![]() ;
;
б)
![]() .
.
Проверить, что уравнение
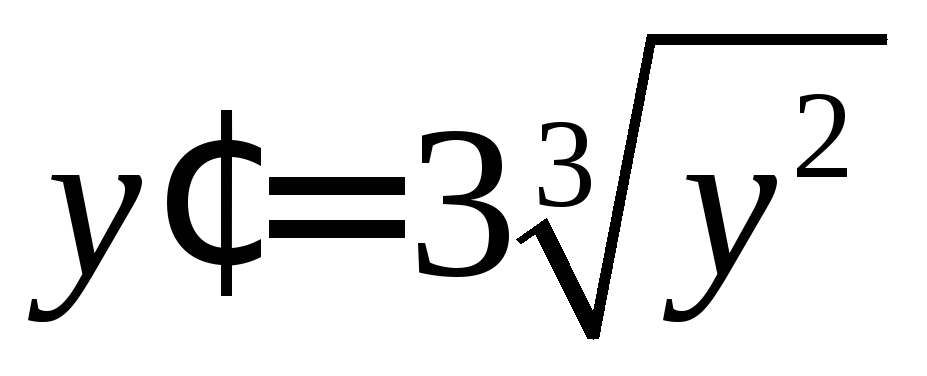 имеет два решения
имеет два решения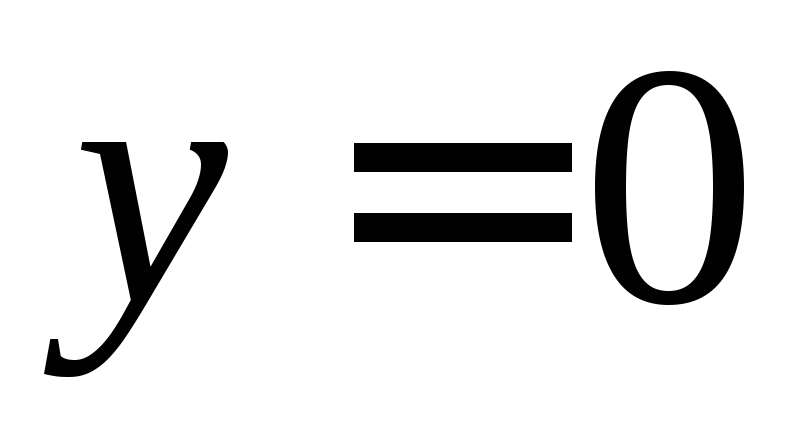 и
и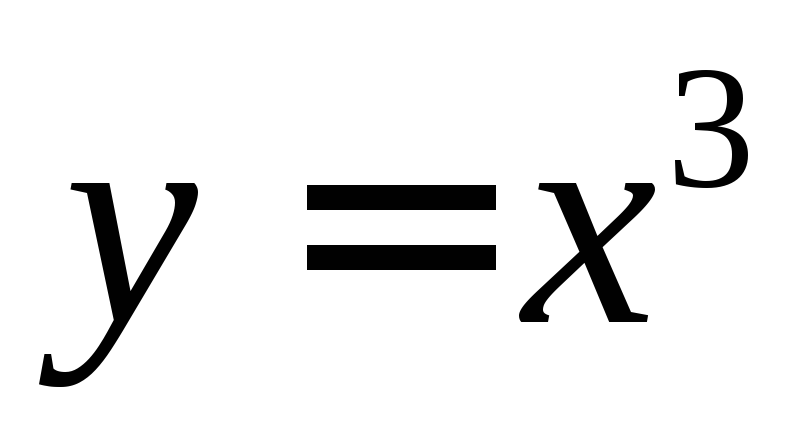 ,
удовлетворяющих начальному условию
,
удовлетворяющих начальному условию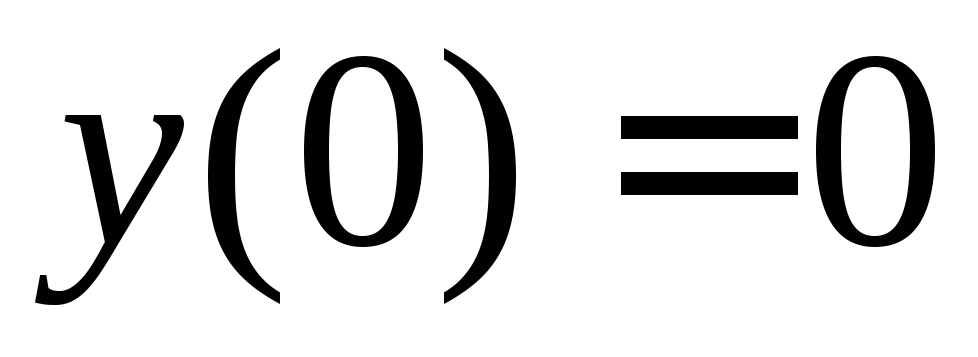 .
Как это согласуется с теоремой
существования и единственности?
.
Как это согласуется с теоремой
существования и единственности?
Проверить, что уравнение
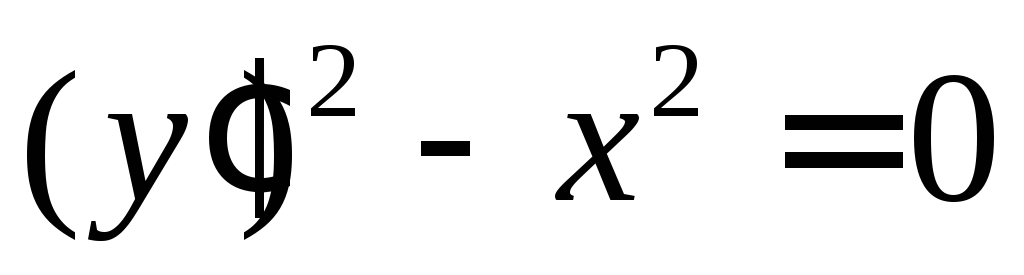 имеет два решения
имеет два решения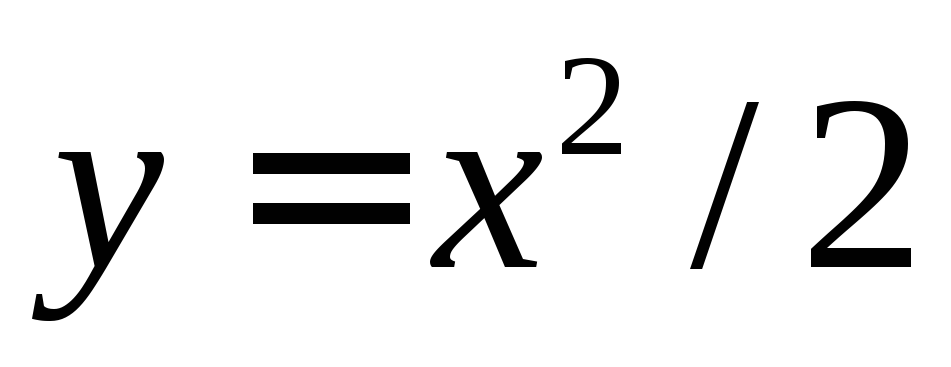 и
и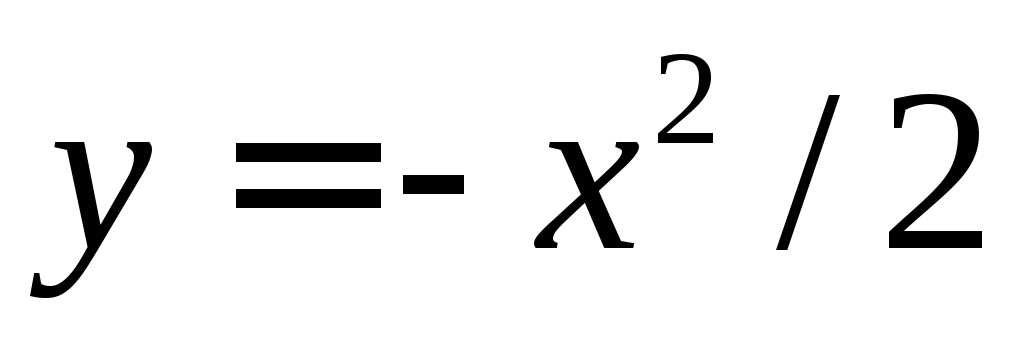 ,
удовлетворяющих начальному условию
,
удовлетворяющих начальному условию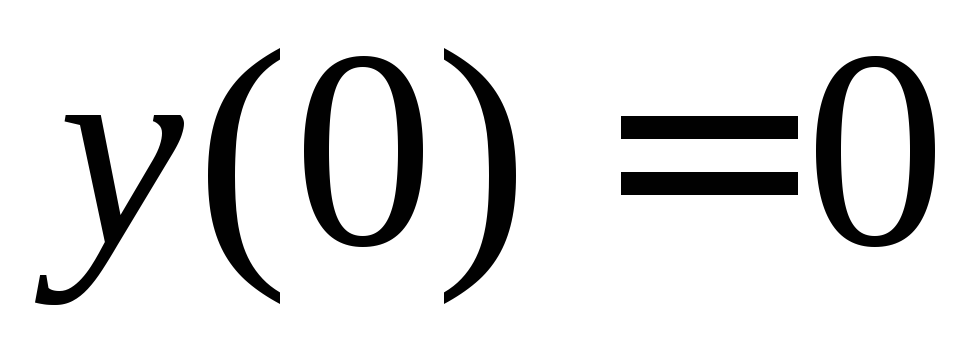 .
Как это согласуется с теоремой
существования и единственности?
.
Как это согласуется с теоремой
существования и единственности?
Уравнения с разделяющимися переменными
Сведения из теории
уравнением с разделяющимися переменными называется уравнение первого порядка, имеющее в нормальной форме вид
![]() ,
,
то
есть уравнение, разрешенное относительно
производной, правая часть которого –
произведение функции от
![]() на функцию от
на функцию от![]() .
.
Метод
нахождения общего решения следующий:
1) представляем производную в виде
отношения дифференциалов
![]() ;
2) делим обе части уравнения на
;
2) делим обе части уравнения на![]() и умножаем на
и умножаем на![]() ;
3) интегрируем обе части полученного
равенства
;
3) интегрируем обе части полученного
равенства
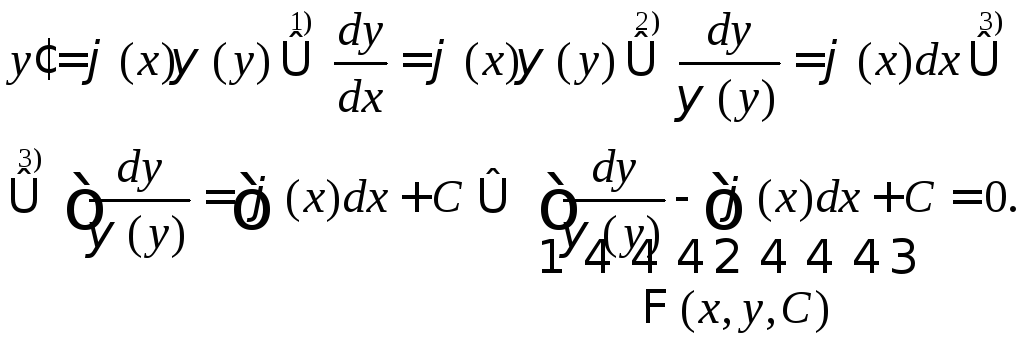
В итоге получим общий интеграл уравнения .
Для
нахождения решения
![]() ,
удовлетворяющему начальному условию
,
удовлетворяющему начальному условию![]()
![]() ,
начиная с пункта 3) интегралы пишем
определенные
,
начиная с пункта 3) интегралы пишем
определенные
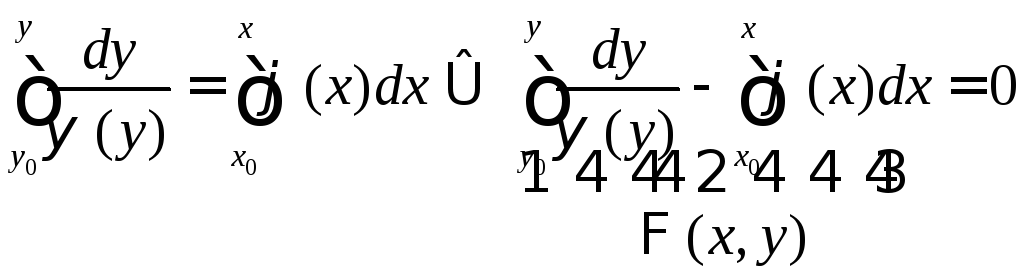 .
.
В
результате получаем уравнение
![]() ,
задающее искомое решение в неявном
виде. Если
,
задающее искомое решение в неявном
виде. Если![]() ,
то очевидно
,
то очевидно![]() решение уравнения , удовлетворяющее
начальному условию
решение уравнения , удовлетворяющее
начальному условию![]() .
.
Примеры решения задач
Найти общее решение уравнения
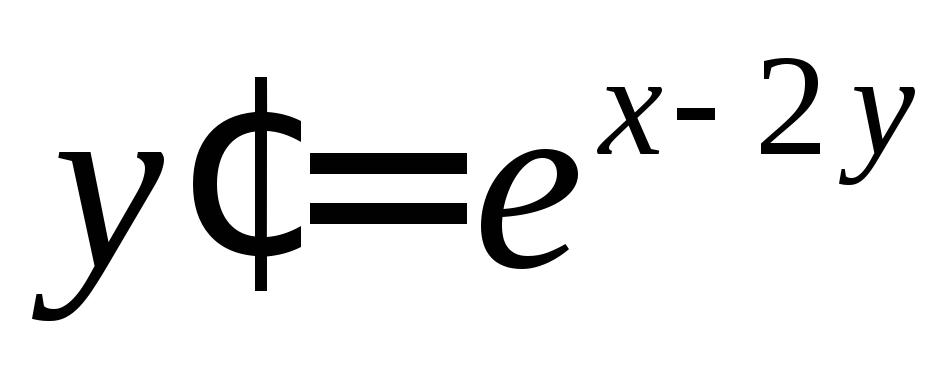 .
.
◄ Перепишем
уравнение в виде
![]() .
Уравнение разрешено относительно
производной, его правая часть –
произведение функции от
.
Уравнение разрешено относительно
производной, его правая часть –
произведение функции от![]() на функцию отy,
следовательно, это уравнение с
разделяющимися переменными. Представляем
на функцию отy,
следовательно, это уравнение с
разделяющимися переменными. Представляем
![]() в виде
в виде![]() ,
умножаем обе части уравнения на
,
умножаем обе части уравнения на![]() ,
делим на
,
делим на![]() :
:![]() .
Интегрируем это равенство
.
Интегрируем это равенство![]() – общий интеграл. Разрешая его относительно
– общий интеграл. Разрешая его относительно![]() ,
получаем общее решение
,
получаем общее решение
![]() или
или
![]() .
.
Так как 2С также произвольная постоянная, то в окончательном ответе мы ее снова обозначили буквой С.►
Найти общее решение уравнения
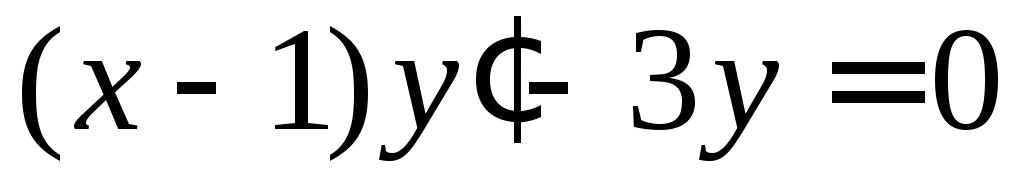 и решение, удовлетворяющее начальному
условию
и решение, удовлетворяющее начальному
условию .
.
◄
Приведем
уравнение к нормальной форме:
![]() .
.
Это уравнение с разделяющимися переменными.
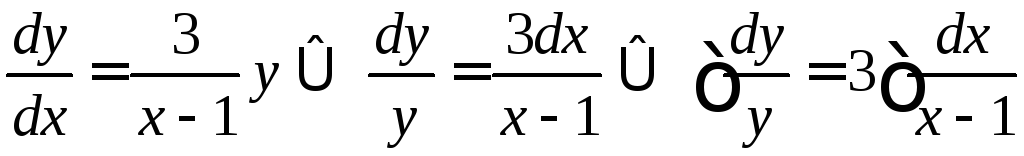 .
.
Функция
![]() принимает все действительные значения,
поэтому постоянную интегрирования
можно представить в виде
принимает все действительные значения,
поэтому постоянную интегрирования
можно представить в виде![]()
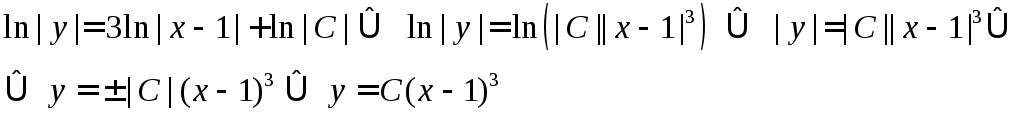
Мы
предполагали, что
![]() ,
но функция
,
но функция![]() дает решение и при
дает решение и при![]() и при
и при![]() ,
в чем легко убедиться, подставляя ее в
уравнение. Таким образом,
,
в чем легко убедиться, подставляя ее в
уравнение. Таким образом,![]() – общее решение уравнения. Подставляя
в него начальные значения
– общее решение уравнения. Подставляя
в него начальные значения![]() ,
получаем
,
получаем![]() .
Поэтому
.
Поэтому![]() – решение, удовлетворяющее начальному
условию
– решение, удовлетворяющее начальному
условию![]() .►
.►
Найти решение задачи Коши
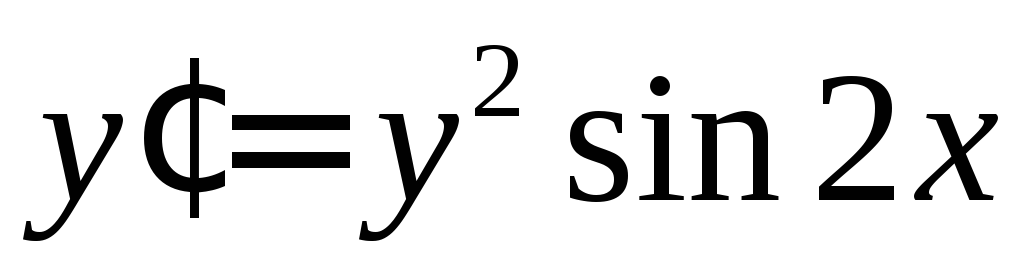 ,
,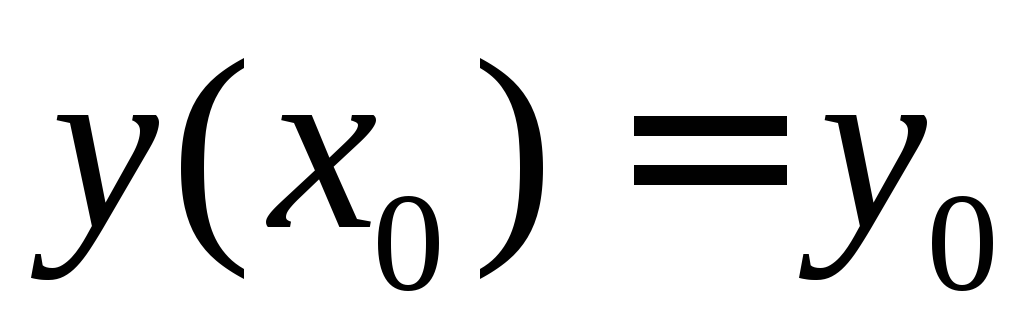 .
.
◄ Разделяем
переменные:
![]() ,
,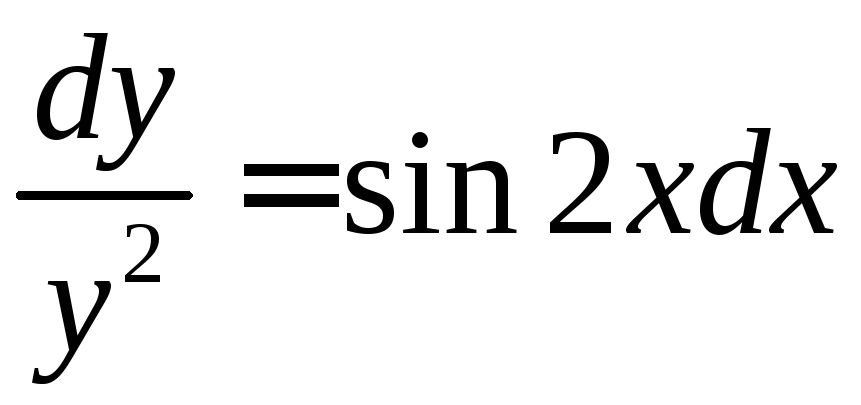 .
При
.
При![]() задача Коши равносильна уравнению
задача Коши равносильна уравнению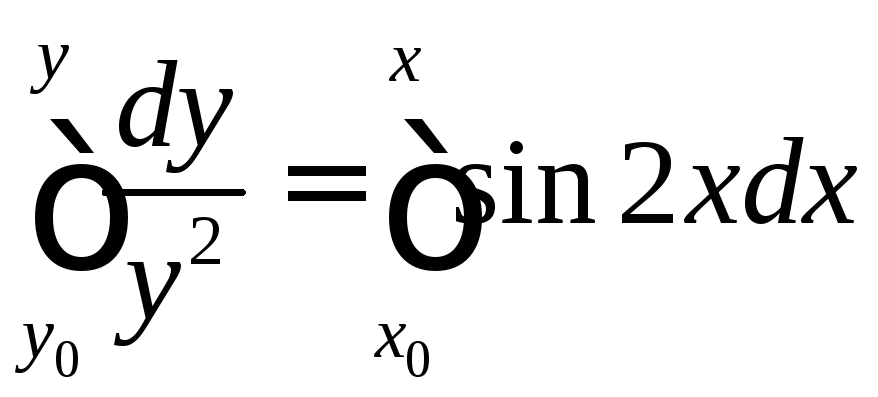 .
Интегрируя, получаем
.
Интегрируя, получаем
 ,
,
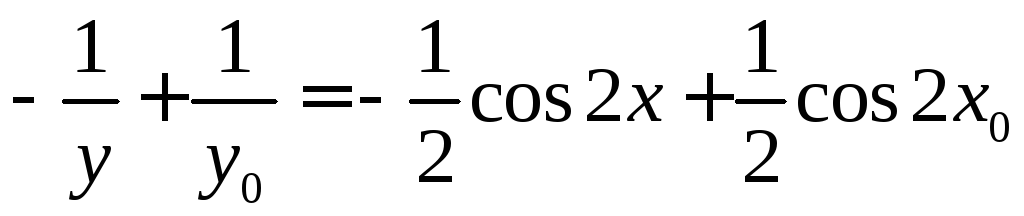 ,
,
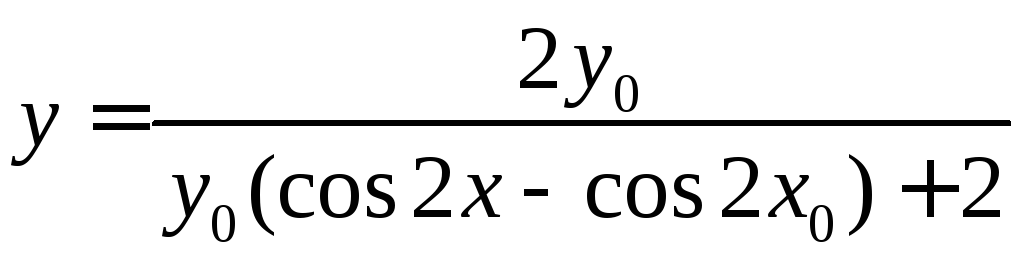 –искомое
решение.
–искомое
решение.
При
![]() решением задачи Коши является функция
решением задачи Коши является функция![]() .►
.►
Задачи для самостоятельного решения
Решить уравнения.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решить задачи.
Тело охладилось за 20 минут от 100°C до 60°C в комнате, где температура 20°C. Найти закон охлаждения тела. Через сколько минут оно остынет до 30°C?
В сосуд, содержащий 10 л воды, непрерывно поступает раствор со скоростью 2л/мин, в каждом литре которого содержится 0,3 кг соли. Поступающий в сосуд раствор перемешивается с водой, и смесь вытекает из сосуда с той же скоростью. Сколько соли будет в сосуде через 5 минут?
Цилиндрический резервуар высотой 6 м и диаметром основания 4 м поставлен вертикально и наполнен водой. За какое время вода, заполняющая резервуар, вытечет из него через отверстие радиуса 1/12 м, сделанного в дне резервуара?
