Запись первых 20 чисел в системах счисления

Десятичные	Двоичные	Восьмеричные	Шестнадцатеричные
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14

2.3. Двоично-восьмеричные и двоично-шестнадцатеричные преобразования

Для преобразования двоичного числа в восьмеричную форму необходимо объединить двоичные цифры в группы по 3 разряда, продвигаясь от разделительной точки (запятой) вправо и влево. При необходимости в начале и в конце исходного числа добавля­ются нули. Затем каждая группа из 3 разрядов заменяется экви­валентной восьмеричной цифрой. Результат будет восьмеричным представлением исходного двоичного числа.

Пример. Преобразовать двоичное число 11011001,1011₂ в восьмеричную форму.

11011001,1011₂ = 011 011 001, 101 100₂ > 331,54₈

^{3 3 1 5 4}

Для преобразования восьмеричного числа в двоичную форму необ­ходимо каждую цифру заменить трехразрядным двоичным числом. При этом незначащие нули отбрасываются.

Пример. Преобразовать восьмеричное число 305,4₈ в двоичную форму.

305,4₈ - 011 000 101, 100₂ = 11000101,1₂

^{3 0 5 4}

Для преобразования двоичного числа в шестнадцатеричную форму необходимо объединить двоичные цифры в группы по 4 разряда, продвигаясь от разделительной точки (запятой) вправо и влево. При необходимости в начале и в конце исходного числа добавля­ются нули. Затем каждая группа из 4 разрядов заменяется экви­валентной шестнадцатеричной цифрой. Результат будет шестнадцатеричным представлением исходного двоичного числа.

Пример. Преобразовать двоичное число 1010111,1101101₂ в шестнадцатеричную форму:

1010111,1101101₂ = 0101 0111, 1101 1010₂ = 57,DA₁₆

^{5 7 D A}

Для преобразования шестнадцатеричного числа в двоичную форму необходимо каждую цифру заменить четырехразрядным двоичным чис­лом. При этом незначащие нули отбрасываются.

Пример. Преобразовать шестнадцатеричное число 2Е5,С₁₆ в двоичную форму:

2Е5,С₁₆ = 0010 1110 0101, 1100₂ = 1011100101,11₂

^{2 Е 5 С}

2.4. Двоичная арифметика

Правила сложения двоичных чисел:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Правила вычитания двоичных чисел:

0 - 0 = 0

1 - 0 = 1

1 - 1 = 0

10 -1 = 1

Правила умножения двоичных чисел:

0 ∙ 0 = 0

0 ∙ 1 = 0

1 ∙ 0 = 0

1 ∙ 1 = 1

Для сложения двух двоичных чисел необходимо применить правило сложения многократно, отправляясь от пары младших (крайних правых) разрядов, как это делается при десятичном сложении. После сложения пары младших цифр и получения значения младше­го разряда суммы складывается следующая пара цифр с учетом пе­реноса из младшего разряда.

Пример:

_{11 1 1}переносы

1011,101₂ слагаемое

1110,001₂ слагаемое

11001,110₂ сумма

Двоичное вычитание обратно двоичному сложению. При вычитании большей цифры из меньшей необходимо произвести "заем" в более старшей соседней позиции. Так, если в позиции n возникает необходимость "заема", то вычитается 1 из (n + 1)-й цифры уменьшаемого, а в позицию n "приносится" величина 2, т.е. основа­ние системы счисления.

Пример:

101 изменение уменьшаемого

… в результате заема

1010,11₂ уменьшаемое

111,01₂ вычитаемое

11,10₂ разность

Умножение двух многоразрядных двоичных чисел проводится аналогично умножению десятичных чисел, т.е. сначала вычисляются частные произведения множимого на отдельные разряды множителя, а затем эти частные произведения суммируются.

Пример:

11,01₂ множимое

101₂ множитель

1101

0000 частные произведения

1101

10000,01 произведение

Двоичное деление также аналогично делению десятичному, т.е. последовательно подбирается очередная искомая цифра частного и на нее умножается делитель, а полученное произведение вычи­тается из делимого для проверки правильности подобранной цифры.

Пример:

10100000 11₂ делитель

11 110101₂ частное

. .

100

11

10

00

. .

100

11

10

00

. .

100

11

1₂ остаток

2.5. Кодирование двоичных чисел - это представление двоичных чисел со знаком.

Применяются следующие коды чисел: прямой, обратный, допол­нительный. Знак "+" кодируется нулем (0), "-" - единицей (1), которые записываются в дополнительном старшем (знаковом) разряде.

Прямой код двоичного числа получается записью в знаковый разряд 0 для положительных и 1 - для отрицательных чисел.

Пример. Представить дробные двоичные числа

Х₁ = +0,1011₂ , Х₂ = -0,01011001₂ в прямом коде.

[Х₁]пр = 0,1011 , [Х₂] = 1,01011001.

Пример. Представить целые двоичные числа

В₁ = +11010; В₂ = -101101 в прямом коде.

[В₁]пр = 0.11010 , [В₂]пр = 1.101101.

В рассмотренных примерах запятая и точка отделяют знако­вые разряды.

Обратный код положительного двоичного числа получается так же, как в прямом коде, т.е.

[X] обр = Xпр, [В] обр = Впр.

Обратный кодотрицательного двоичного числа образуется записью в старшем (знаковом) разряде 1 и заменой в разрядах двоичного числа нулей на единицы, а единиц на нули.

Пример. Представить дробные двоичные числа

Х₁ = +0,1001₂ ; Х₂ = -0,01101 в обратном коде.

[Х₁]обр = 0,1001 [Х₂]обр = 1,10010

Пример. Представить целыечисла

В₁= +111001₂; В₂= -110011011₂

[В₁]обр = 0.111001; [В₂]обр = 1.001100100.

Дополнительный кодотрицательного двоично­го числа получается из обратного кода этого числа прибавлением единицы к младшему разряду.

Пример. Представить дробные двоичные числа

Х₁= +0,1001₂; Х₂= -0,01101₂в дополнительном коде

[Х₁]доп = 0,1001; [Х₂]доп = [Х₂]обр + 0,00001;

[Х₂]обр = 1,10010;

[Х₂]доп = 1,10010

0,00001

1,10011

Пример 2. Представить целые двоичные числа

В₁= +111001₂; В₂= -110011011₂

[В₁]доп = 0.111001; [В₂]доп = [В₂]обр+ 0.000000001.

[В₂]обр = 1.001100100

[В₂]доп = 1.001100100

0.000000001

1.001100101

Представление ±0 в прямом, обратном и дополнительном кодах приведено в табл.2.5.1

Таблица. 2.5.1

Значение	Прямой код	Обратный код	Дополнительный код
+0	0.00…0	0.00…0	0.00…0
-0	1.00…0	1.11…1	0.00…0

Неоднозначность представления нуля в обратном коде (см. табл. 2.5.1) является одним из недостатков обратного кода.

2.6. Сложение и вычитание коди­рованных чисел производится при одинаковом их представлении, для чего числа со знаком перед кодированием вы­равниваются по числу разрядов добавлением нулей справа (для дробной части) и слева (для целой части) исходных чисел.

Сложение двоичных чисел в прямом коде, когда у слагаемых одинаковые знаки, осуществляется суммирова­нием их модулей по правилам двоичного сложения и присвоением сумме знака слагаемых.

Пример. Выполнить сложение в прямом коде следующих двоич­ных чисел:

Х₁ = +0,001₂; Х₂ = +0,110₂; У₁ = -0,0100₂; У₂ = -0,1001₂;

А₁ = +1110₂; А₂ = +1111₂; В₁ = -1000₂; В₂ = -1011₂.

а) /Х₁/ = 0,001 б) /У₁/ = 0,0100

/Х₂/ = 0,110 /У₂/ = 0,1001

/Х₁/ + /Х₂/ = 0,111 /У₁/ + /У₂/ = 0,1101

[Х₁ + Х₂]пр = 0,111 [У₁ + У₂]пр = 1,1101

в) /А₁/ = 1110 г) /В₁/ = 1000

/А₂/ = 1111 /В₂/ = 1011

/А₁/ + /Х₂/ = 11101 /В₁/ + /В₂/ = 10011

[А₁ + А₂]пр = 0.11101 [В₁ + В₂]пр = 0.111

В связи с громоздкостью реализации операции вычитания в прямом коде ее в вычислительных устройствах не применяют, заменяя операцией сложения с использованием обратного или дополнительного кодов.

Сложение двоичных чисел в дополнительном коде осуществляется суммированием кодов этих чисел по правилам двоичного сложения, разряд за разрядом, вклю­чая старшие, знаковые разряды кодов. При этом перенос из зна­кового разряда отбрасывается, а результат получается в дополнительном коде.

Пример. Выполнить сложение в дополнительном коде следующих двоичных чисел:

Х₁ = +0,0011₂ и У₁ = +0,101₂; Х₂ = +0,0101₂ и У₂ = -0,0011₂;

Х₃ = +0,0011₂ и У₃ = -0,0101₂; Х₄ = -0,0011₂ и У₄ = -0,0101₂;

А₁ = -011₂ и В₁ = -110₂; А₂ = +110₂ и В₂ = -011₂;

А₃ = -011₂ и В₃ = -100₂.

а) /Х₁/доп = 0,0011 б) /Х₂/доп = 0,0101

/У₁/доп = 0,0101 /У₂/доп = 1,1101

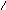[Х₁ + У₁]доп = 0,1000 [Х₂ + У₂]доп = 10,001 =

= 0,001

(единица переноса теряется)

в) /Х₃/доп = 0,0011 г) /Х₄/доп = 1,1101

/У₃/доп = 1,1011 /У₄/доп = 1,1011

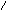[Х₃ + У₃]доп = 1,1110 [Х₄ + У₄]доп = 11,1000 =

= 1,1000

(единица переноса теряется)

д) /А₁/доп = 0.011 е) /А₂/доп = 0.110

/В₁/доп = 1.010 /В₂/доп = 1.101

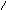[А₁ + В₁]доп = 1.101 [А₂ + В₂]доп = 10.011 =

= 0.011

(единица переноса теряется)

ж) /А₃/доп = 1.101

/В₃/доп = 1.100

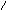[А₃ + В₃]доп = 11.001 = 1.001 (единица переноса теряется)

Сложение двоичных чисел в обратном коде осуществляется суммированием кодов слагаемых по правилам двоичного сложения, включая знаковые разряды. При этом перенос из знакового разряда прибавляется к младшему раз­ряду суммы (так называемый циклический перенос), а результат получается в обратном коде.

Пример. Выполнить сложение в обратном коде следующих двоичных чисел:

Х₁ = +0,01011₂ и У₁ = -0,10101₂;

Х₂ = +0,10111₂ и У₂ = -0,01010₂;

А₂ = +1001₂ и В₂ = -1110₂; А₂ = -0110₂ и В₂ = -1000₂;

а) [Х₁]обр = 0,001 б) [Х₂]обр = 0,0100

[У₁]обр = 0,110 [У₂]обр = 0,1001

[Х₁ + У₁]обр = 1,10101 1 0,01100

1 = циклический

перенос

[Х₂ + У₂]пр = 0,01101

в) [А₁]обр = 0.1001 г) [А₂]обр = 1.1001

[В₁]обр = 1.0001 [А₂]обр = 1.0111

[А₁ + В₁]обр = 1,10101 1 1,0000

1 = циклический

перенос

[А₂ + В₂]пр = 1.0001

Обращение положительного числа М, имеющего (n - 1)-разрядное представление, - это результат вычисления по формуле q^n-1 - 1 - /M/,

где q - основание системы счисления.

(n - 1) - разрядное представление чисел возникает при кодировании отрицательных чисел, когда старший (знаковый) раз­ряд содержит 1.

Относительно обратного кода числа со знаком, обращением называют операцию, состоящую в применении (1) к величинной части кода и в замене значения знакового разряда на противоположное. Для обращения двоичных чисел, представленных в обратном коде, необходимо заменить каждый 0 на 1, а каждую 1 на 0, включая знаковый разряд.

Пример. Получить обращение чисел, представленных в двоич­ном обратном коде:

[Х]обр = 0,01011; [У]обр = 1,01101;

[А]обр = 0.00101; [В]обр = 1.11001.

Таблица 2.6.1

Обозначение	Код	Обращение
Х	0,01011	1,10100
У	1,01101	0,10010
А	0.00101	1.11010
В	1.11001

Дополнение положительного числа М, имеющего (n - 1)-разрядное представление, - это результат вычисления по формуле:

q^n-1 - /M/,

Применительно к дополнительному коду взятием дополнения называют операцию, состоящую в применении вычисления (2) с величиной части кода и инвертировании значе­ния знакового разряда. Для получения дополнения двоичных чи­сел, представленных в дополнительном коде, необходимо сначала выполнить обращение путем замены 0 и 1 в коде соответственно на 1 и 0, а затем прибавить к младшему разряду результата 1.

Пример. Получить дополнение чисел, представленных в дво­ичном дополнительном коде:

[Х]доп = 0,10110; [У]доп = 1,10001;

[А]доп = 0.10100; [В]доп = 1.11100.

Таблица 2.6.2

Обозначение	Код	Обращение	Дополнение
Х	0,10110	1,01001	1,01010
У	1,10001	0,01110	0,01111
А	0.10100	1.01011	1.01100
В	1.11100	0.00011	0.00100

Для вычитания двоичных чисел, представленных в дополнительном коде, необходимо сначала взять дополнение вычитаемого, а затем сложить это дополнение с кодом уменьшаемого.

Пример. Выполнить вычитание для следующих чисел, представ­ленных в двоичном дополнительном коде: