ПЗ(Фінал_суббота)v3

починало перетікати з більш обжатих місць, нерівномірно розподіляючись по перетину панелі. Це призвело до місцевого збільшення об'ємного змісту сполучного у верхніх шарах, викликаючи їх велику усадку в процесі охолодження. Дослідження нерівномірного розподілу сполучного в даному випадку проводилося як за допомогою, розробленої в розділі 1 методики, так і методу скінченних елементів (рис. 6). різниця між отриманими в ході розрахунків величинами прогинів склала близько 6 % і збіглася з отриманими на виготовленої панелі. Таким чином, проведене дослідження дозволило виробити рекомендації щодо оптимізації структури композиту з метою зниження залишкових напруг і кривизни, оцінити ефективність використання технологічних прийомів, оцінити вплив недосконалостей технологічного процесу на залишкове напруженодеформований стан, оцінити вплив вязкоупругого характеру поведінки механічних властивостей полімерного сполучного.

3. Класифікатор композиційних панелей 3.1.Формалізація структури класифікатора

Зазвичай під кластером розуміється така непорожня підмножина досліджуваної множини, в якій складові його елементи більш близькі один до одного, ніж до інших елементів, що не входять в цю підмножину [21]. Наприклад, нехай множина N складається з двох підмножин ωi - зафарбовані точки його елементи і ωj - незафарбовані точки (рис. 3.1)

Рис. 3.1. Підмножини ωi і ωj піддаються класифікації, за допомогою поняття близькості.

З малюнка 3.1 можна зробити висновок, що підмножини ωi і ωj становлять два класи об'єктів, досить далеко віддалених один від одного і тому розділами[28].

Для формалізації цієї процедури необхідно виконати наступні дії:

-Аналітичним шляхом описати елемент множини (образ);

-Користуючись яким-небудь правилом, зробити поділ елементів на непересічні підмножини (кластери);

-Визначити вирішальну функцію, що дозволяє при завданні координат образу встановити клас, до якого належить даний образ.

Опис образів може здійснюватися двома методами:

-Із застосуванням теорії матриць суміжності;

-З використанням теорії графів.

У даній роботі використаний графічний метод опису образів, з застосуванням довічних деревовидних графів, як більш наочний і дозволяє здійснювати кодування елементів множини двійковими числами.

Відношення елементів безлічі до того чи іншого підмножині виконано за критерієм мінімуму відстані. Нехай задано множину N образів {Х1, Х2,… Хn}.

Центр першого кластера Z1 збігається з будь-яким із заданих образів в кластері

і крім цього визначається довільна невід'ємна порогова величина Т. Для зручності можна вважати, що Z1 = Х1. Потім обчислюється відстань d21 між

чином Х2 і центром кластера Z1 за формулою:

(3.1)

де Х - вектор i-го образу, який визначається як

(3.2)

тут кожен елемент хі- проекція образу X на відповідну вісь координат. Оскільки опис образів X буде проводитися в двійковій системі координат, координатні змінні образу X прийматимуть значення «1» або «0»

Якщо відстань d12 більше значення порогової величини T, то утворюється новий центр кластера Z2=Х2. В іншому випадку образ включається в кластер, центром якого є Z1.

Вирішальна функція буде здаватися лінійним рівнянням виду:

(3,3)

де вектор w0=(w1, w1…wn) називається ваговим або параметричним. На рис. 3.2 розглянуто приклад простої вирішальної функції для випадку поділу класів

ω1 і ω2.

(2,4)

Рис. 3.2 Приклад розрахукової функції Рівняння (3,3) представим у заступному вигляді:

(2,5)

У залежності (2,5) Х=(х1, х2,…хп, 1) – поповнений вектор образів, а w0=(w1, w1…wn) – вектор вагів.

Для пояснення алгоритму кластеризації розглянемо приклад. нехай маємо двійковий деревовидний граф (рис. 3.3), вершинами якого є ознаки образів, а ребра встановлюють зв'язки між цими ознаками. Граф має чотири рівні:

верхній рівень відповідає корені двійкового дерева, а три нижніх вказують на ознаки, якими володіють образів Х1, Х2,…Х8.

Рис. Двійковий деревовидний граф Наявність ознаки на певному рівні фіксується затемненим кружком, а його

відсутність вказано світлим кружком. Відповідно до прийнятим позначенням проводиться кодування образів у двійковому коді:

Х1(111); Х2(110); Х3(101); Х4(100); Х5(011); Х6(010); Х7(001); Х8(000).

Проведемо кластеризацию образів на два класи ω1 і ω2- За центр кластеризації образів класу ω1 приймемо Z1=Z4, а образів класу ω2- Z2= X5. При цьому порогову величину призначимо Т-1 (табл. 3.1)

Табл. 3.1 Коди образів відстані між ними

Відповідно до прийнятих умовами образи розподілилися на класи: ω1 {(000), (101), (100), (110)} і ω2: {(001), (010), (011), (111) }.

На рис. 3.4 представлені класи ω1 і ω2 у тривимірному просторі ознак.

Рис. 3.4. Графічне представлення поділу образів на класи Тут кожному образу відповідає своя вершина тривимірного куба.Уявити

образи на кубі, розмірністю вище трьох, графічно не представляється можливим, тому надалі образи з більшоюрозмірністю будуть представлятися виразами в двійковим коді, декожному розряду образу буде відповідати свій ознака.Визначити вирішальну функцію безпосередньо по залежності (3.3) досить складно, тому що в більшості прикладних задач при великій кількості вимірів класи в явному вигляді площинами не роздільні, тому вдаються до наближення (апроксимації) і вирішальних функцій. Вирішальні функції еквівалентні Байєсовому класифікаційному правилу [106], згідно з яким:

(3,6)

де р (Х ωі)-ймовірність попадання образу X в клас ωі; р (ωі) - імовірність появи класу ωі;

У зв'язку з цим функцію (3.3) представимо в наступному вигляді:

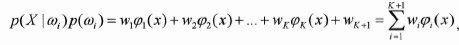(2,7)

Де φ(х), і=1, 2,…,К,дійсне означення функції Х, φК+1(х)=1, а К+1 - число членів розкладання.

Прийнявши, що р(ω1)=р(ω2)=1/2, отримаємо наступні вирішальні функції:

Вирішальну функцію, що забезпечує розділення двох класів, отримаємо наступним чином:

(3,9)

Звідси остаточно отримаємо

Перевірка показує, що

D(X)>0 для всіх образів класу ω1;

D(X)<0 для всіх образів класу ω2.

На закінчення необхідно відзначити, що виведена вирішальна функція d(X) має сенс тільки для двійкових образів X. Функція d (X) для даного прикладу має тільки вісім значень - по одному на кожен з восьми різних двійкових образів, які можуть існувати в тривимірному просторі.

3.2.Ознаки, що характеризують монолітні композиційні панелі

Згідно з попереднім параграфом побудова класифікатора монолітних панелей починається з опису всього їх різноманіття при допомозі графів. Для побудови графів, що відображають структуру панелей, в першу чергу необхідно мати уявлення про основні ознаки, що характеризують ту чи іншу панель. Це питання обговорюється в даному параграфі.

Виділяючи ознаки, що характеризують панель, інтерес представляють в першу чергу ті, які прямим або непрямим чином впливають на геометричне точність деталі в процесі виготовлення і складання.

Серед існуючого різноманіття ознак, насамперед можна виділити ті, які визначають геометричні властивості деталі, конструктивні властивості полотна і конструктивні властивості силового набору. Таким чином, глобальний класифікаційний граф ознак панелей G(U) повинен складатися з трьох подграфiв, що можна записати виразом:

G(U)=(A, B, C), (3.10)

де А - підграф, що визначає геометричні властивості; В - підграф, що визначає конструктивні властивості полотна панелі;

С - підграф, що визначає конструктивні властивості силового набору панелі. Розглянемо ознаки, що характеризують геометричні властивості подграфа А. Основний геометричній характеристикою поверхні панелі є ступінь повної кривизни:

(3,11)

де Кпозд - головна кривизна в поздовжньому напрямку панелі; Кпопер - головна кривизна в поперечному напрямку панелі; b - ширина панелі;

V = 100/b - коефіцієнт пропорційності.

У відповідності зі значеннями ступеня кривизни виділяються панелі наступних геометричних властивостей:

1.K=V*(Кпозд*Кпопер)=0. До цього класу відносяться панелі одинарної кривини (рис. 3.4), а саме:

-Плити (Кпозд=Кпопер=0);

-Циліндр (Кпозд=0, Кпопер=const або Кпозд=const, Кпопер=0);

-Конус (Кпозд=0, Кпопер≠const або Кпозд≠const, Кпопер=0).

Рис. 3.5. Панелі одинарної кривизни: а - циліндрична, б – конічна

2.K=V*(Кпозд*Кпопер)≠0 До цього класу відносяться панелі подвійний кривини (рис. 3.6), а саме:

-Опуклий парус (Кпозд* Кпопер>0 при Кпозд і Кпопер>0);

-Ввігнутий парус (Кпозд* Кпопер>0 при Кпозд і Кпопер<0);

-Сідло (Кпозд* Кпопер<0 при Кпозд<0 і Кпопер>0 або Кпозд>0 і Кпопер<0);

Рис. 2.6. Панелі подвійної кривизни а - опуклий «парус»; б - увігнутий «парус»; в - «сідло»

Можливі значення параметра К (рис. 3.7) для панелей подвійний кривизни знаходяться в межах від -3 до +3 [60]. Монолітні композиційні панелі із значеннями критерію більше 3 і менше -3 в конструкції панелей практично не застосовуються, так як при їх формоутворенні поширеними в промисловості методами утворюються деформації більше граничних.

Рис. 3.7. Зміна ступеня кривини К (за інших співпадаючих ознаках) панелі типу «парус» Геометричний класифікатор повинен враховувати технологічні можливості

виготовлення панелей з відповідною кривиною. У відповідно до цього, за ступенем повної кривизни монолітні панелі в геометричному класифікаторі поділені за такими ознаками:

-Панелі нульової ступеня повної кривизни К = 0;

-Панелі, у яких 2 <К <3;

-1.25<К<2;

-0<К<1.25; -1.25<К<0; -2<К<-1.25; -3<К<-2.

Крім цього у панелей з нульовим ступенем кривизни введені ознаки, коли:

-Кпозд=Кпопер=0

-Кпозд=0, Кпопер=const або навпаки.

Таким чином, в геометричному класифікаторі А передбачено дев'ять ознак, що відображають геометричні властивості монолітних панелей. У параграфі 3.4 буде показано, що ці ознаки тісно пов'язані з технологічними прийомами виготовлення панелей.

До ознак, які характеризують конструкцію полотна панелі (подграф В), віднесемо вид в плані, відношення довжини до ширини, сталість товщини полотна, граничні значення товщини полотна.

Вид в плані.

Найбільш поширені види в плані полотна панелі, прийняті в як ознак, представлені на малюнку 3.8:

Рис. 3.8. Вид панелі в плані: а - паралелограм, б-трапеція Габарит по довжині.

Визначальними ознаками монолітних панелей по довжині приймаємо:

-Відношення довжини панелі до ширини L / В <5; 59

-Відношення довжини панелі до ширини L / В> 5. Сталість товщини полотна (рис. 3.9).

Ознаки:

-Товщина полотна постійна;

-Товщина полотна непостійна (клинова або ступінчаста).

Рис. 3.9. Ознака сталості товщини полотна а - постійна, б - ступінчаста або клинова Визначальними ознаками монолітних композиційних панелей по товщині полотнабудуть:

-Товщина А;

-Товщина А +t, де (t- порогова величина, що визначає зміну режиму обробки. Таким чином, в класифікаторі по конструкції полотна панелі В введено вісім конструктивних ознак.

Подграф С, що характеризує силовий набір панелі, визначається наступними ознаками: вид силового набору в плані, форма перерізу стрингера, розміри поперечного перерізу стрингера, вирізи на полотні, наявність локальних жорсткостей.

Вид силового набору в плані (рис. 3.10):

-Без силового набору;

-Стрингерний силовий набір;

-Вафельний силовий набір.

Рис. 2.10. Силовий набір в плані а - стрингерний; б, в – вафельний Форма перерізу стрингера (рис. 3.11):

-Симетрична;

-Несиметрична;

Рис. 2.11. Перетин силового набору а, б-набір симетричного типу; в - несиметричного типу Розміри поперечного перерізу стрингера:

-постійні;

-змінні.

Вирізи на полотні (рис. 3.12):

-є;

-не маються.

Рис. 3.12. Вирізи на полотні монолітної панелі

Наявність локальних жорсткостей:

-Є;

-Не маються.

Таким чином, на підграфі С виділено одинадцять ознак. Завершуючи параграф, ще раз варто підкреслити, що всі зазначені ознаки панелі мають вплив на точність її геометричної форми, склад і порядок операцій технологічного процесу.

3.3 Конструктивно-геометричний класифікатор монолітних панелей

На підставі виділених у попередньому розділі ознак побудований загальний класифікаційний граф (рис. 3.13), що складається з геометричного А конструктивних В і С підграфів, де С = (С1, С2, СЗ).

Таким чином, класифікатор G (U) можна представити як область, всередині якої знаходяться області А, В, С1, С2 і СЗ (рис. 3.14)

Рис. 3.14. Подання класифікатора, як множини областей При цьому: