экстраполяция ричардсона

Оглавление

Введение 3

1 Экстраполяция Ричардсона 4

2 Метод Грэгга - Булирша – Штера 15

3 Метод Ромберга 17

Заключение 19

Список источников 20

Введение

В настоящее время методы экстраполяции широко применяются для решения обыкновенных дифференциальных уравнений, требующих высокой точности решения. Достоинство методов экстраполяции заключается прежде всего в том, что при их использовании не требуется многократного перевычисления правых частей дифференциальных уравнений. Это особенно важно, когда правые части уравнений достаточно сложны. Разработкой методов экстраполяции занимались такие известные специалисты, как Л. Ричардсон, Р. Булирш, Дж. Штер и др.

1 Экстраполяция Ричардсона

Мы уже неоднократно видели, что погрешность разностных формул для дифференцирования и интегрирования зависит от расстояния h между соседними узлами; в приближенных формулах хорошей точности эта погрешность есть О (h2) или О (h4).

Так, вычисляя значения производных через центральные разности с учетом первых членов разложения или интегрируя по формуле трапеций, мы допускаем погрешность порядка h'2. Учет вторых членов разложения при вычислении производных и интегрирование по формуле Симпсона позволяет снизить величину погрешности до O (Л4).

Порядок погрешности и в том и в другом случае определяется главным из отброшенных членов разложения. Сама же погрешность, как легко видеть, может быть представлена рядом:

Если погрешность есть О (h⁴), то f₁(x) = 0.

Если мы вычисляем разностным методом какое-либо выражение, не зависящее от х (например, определенный интеграл), то коэффи­циенты разложения будут, очевидно, постоянны, и оно принимает следующий вид:

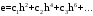
Сказанное относится и к случаю, когда вычисления ведутся при раз­личных значениях h, но в одной и той же точке х.

В этом параграфе мы покажем, как, зная форму ряда, в кото­рый разлагается погрешность, можно улучшить точность вычислений, затратив немного дополнительного труда.

Предположим, например, что значение некоторого интеграла А вычислено по формуле трапеций при двух различных шагах:

где n₁ n₂— числа интервалов. Полученные приближенные значения обозначим соответственно через А_n1 и А_n2. Если h₁ и h₂ малы на­столько, что можно пренебречь всеми членами разложения (9.2), кроме первого, то

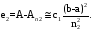
Исключив из этих соотношений неизвестную нам константу с_х(b—a)², получим так называемую экстраполяционную формулу порядка h²:

Если отброшенные члены разложения (9.2) малы, то эта формула дает значительное повышение точности.

Так, например, взяв приближенные значения А₂— 1,571 и А₄— 1,896 интеграла (е) найдем:

Погрешность значения A_2,4 составляет 0,2% вместо 21% и 5,2% в A₂ и A₄ соответственно. При n= 4 и n = 6 получим аналогичным образом:

с погрешностью 0,02%.

Коэффициенты формулы зависят, как легко видеть, только от отношения n₂/n₁. Значения этих коэффициентов приведены в таблице.

Зная три приближенных значения А_n1, А_n2, А_n3 величины А, вычи­сленные с шагами h₁ h₂, h₃, обратно пропорциональными n₁, n₂, n₃, мы можем учесть два первых члена разложения. Для этого напишем

Таблица 1. Экстраполяционнные коэффициенты порядка h²

n2/n1	α1	α2
2/1	— 0,3333333333	1,3333333333
3/2	— 0,8	1,8
4/3	— 1,2857142857	2,2857142857
5/4	— 1,7777777778	2,7777777778
6/5	— 2,2727272727	3,2727272727
7/6	— 2,7692307692	3,7692307692
8/7	— 3,2666666667	4,2666666667
3/1	— 0,125	1,125
5/3	— 0.5625	1,5625
7/5	—1,0416666667	2,0416666667

Исключив из этих соотношений неизвестные константы с₁(b— a)'² и c₂(b — a)⁴, получим экстраполяционную формулу порядка (h², h⁴):

Коэффициенты β_t, β₂, β₃, соответствующие различным отношениям n₃/n₂/n₁ приведены в. таблице 2.

Таблица 2. Экстрапоялционные коэффициенты порядка (h², h⁴)

n3/n2/n1	P1	Р2	Р3
3/2/1	0,0416666667	— 1,0666666667	2,025
4/2/1	0,0222222222	— 0,4444444444	1,4222222222,
4/3/2	0,2666666667	— 2,3142857143	3,0476190476
5/4/2	0,6349206349	— 2,3703703704	3,3068783069
5/4/3	0,7232142857	— 4,0634920635	4,3402777778
6/5/4	1,4222222222	— 6,3131313131	5,8909090909
7/6/5	2,3674242424	— 9,0629370629	7,6955128205
8/7/6	3,5604395604	—12.3128205128	9.7523809524
5/3/1	0,0052083333	— 0,6328125	1,6276041667
7/5/3	0,1265625	—1,6276041667	2,5010416667

ТТТ

Взяв приближенные значения А₂, A₄, А₆ интеграла (е) и выбрав коэффициенты β, соответствующие отношению 6/4/2 = 3/2/1, из таблицы 2 найдем

Погрешность составляет 0,005%

Предположим теперь, что погрешность разностной формулы есть O(h⁴). Тогда в разложении коэффициент c₁=0 в этом случае погрешности двух различных приближенных значений (при n=n₁ и n=n₂) равны:

Пренебрегая всеми членами правой части, кроме первого, как и ранее,

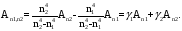
Это – экстраполяционная формула порядка h⁴. Коэффициенты приведенны в таблице 3

Таблица 3. Экстраполяционные коэффициенты порядка h⁴

n2/n1
2/1	— 0,0666666667	1,0666666667
3/2	— 0,2461538462	1,2461538462
4/3	— 0,4628571429	1,4628571429
5/4	— 0,6937669377	1,6937669377
6/5	— 0,9314456036	1,9314456036
7/6	— 1,1728506787	2,1728506787
8/7	—1,4165191740	2,4165191740
3/1	— 0,0125	1,0125
5/3	— 0,1488970588	1,1488970588
7/5	— 0,3519144144	1,3519144144

Применим выведенную формулу для уточнения, приближенных значений А₂ и A₄ интеграла (е), найденных по формуле Симпсона, т. е. с погрешностью порядка h¹. Взяв из таблицы 3 коэффициенты для случая n₂/n₁=2/1, найдем:

Погрешность 0,1%.

Еще один пример: найдем приближенные значения производной функции Бесселя J_1/4(x) в точке х = 0,5 с помощью центрального разностного оператора.

при h — 0,4; 0,2; 0,1; 0,05. Эти значения выписаны в третьем столбце таблицы 4. Рядом Приведены соответствующие погрешности (истинное значение J_1/4(0,5) = 0,21909). Так как при вычислении производной через центральные разности погрешность разлагается в ряд, то для увеличения точности (при фиксированном х) можно воспользоваться экстраполяционными формулами порядка h² или (h², h⁴). Выбирая значения коэффициентов соответственно для n₂/n₁=2/1 и n₃/n₂/n₁ = 4/2/1 из таблиц 1 и 2, получим резуль­таты, приведенные в таблице 4. Там же выписаны соответствующие погрешности (в % к истинному значению 0,21909).

Описанными экстраполяциями можно пользоваться лишь в тех случаях, когда вычисленные значения приближаются к истинному монотонно. В противном случае нельзя пренебрегать высшими членами разложения.

Таблица 4. результаты

Вычисленное значение					Экстраполяция порядка h2				Экстраполяция порядка (h2, h4)
	n	J1/4(0,5)	e(%)	n		J1/4(0,5)	e(%)	n		J1/4(0,5)	e(%)
0,4	1	0,30377	+ 38,6	2/1		0,20994	-4,2	4/2/1		0,21931	+0,10
0,2	2	0,23340	.+6,5	4/2		0,21873	-1,6	8/4/2		0,21908	-0,004
0,1	4	0,22240	+ 1,5	8/4		0,21906	-0,013
0,05	8	0,21990	+ 0,37

Рассмотрим задачу Коши

y¢(x) - f (x, y(x)) = 0 xÎ[a, b] , y(a) = y .

Для нахождения решения задачи с помощью экстраполяции Ричардсона решение ищется не на всем интервале интегрирования, а на последовательных его подынтервалах ( x_n,x_n+1 ) .

Основная идея экстраполяции Ричардсона состоит в рассмотрении решения n+1 y сходящейся дискретной задачи, как функции от N вычислений нескольких значений и их интерполяции подходящей функцией y(N) от аргумента N . Значения могут быть получены с различным шагом интегрирования. Предельный переход при N бесконечном приводит к точному решению y(x_n+1) исходной задачи

Рисунок 1. Интерполяция значений

В общем случае, если имеется некоторая функция F(h) , которая может быть представлена в виде степенного ряда

стандартная процедура экстраполяции Ричардсона состоит в исключении главных членов ряда (2.90), который вычисляется для (i = 0, 1, ... , m) , где h – длина шага (малый параметр), который используется для управления процессом вычисления.

Если функцию F заменить интерполяционным полиномом P^{[ j ]} (h_i), у которого P^[0] = F(h_i) , то используемый алгоритм экстраполяции называют алгоритмом Невилла, представленным в виде следующей таблицы:

Таблица заполняется столбец за столбцом следующим образом:

Произведя замену h_i и h_i+j на h_i-h и h_i+j –h получим интерполяционный полином P^{[ j ]} (h) степени j для функции F(h_i ), так как

Из формулы (2.92) непосредственно следует, что погрешность в

алгоритме экстраполяции дается формулой

где коэффициент E^{[ j ]} в остаточном члене может быть вычислен следующим образом

где (ξ) i x содержится в интервале (0, max( h₁,..., h_i+j )).

Целесообразно представить последовательность { h_i} в виде

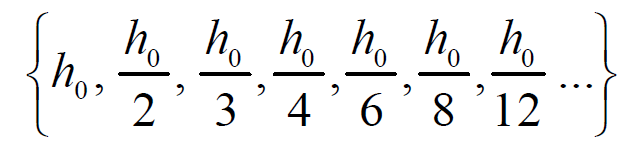
так как эта последовательность приводит к устойчивому алгоритму и экономична в смысле объема вычислений. Следует отметить, что эффективность алгоритма экстраполяции зависит от способа разложения функции F(h) в ряд. Если известно, что разложение имеет вид

тогда формулы (2.92) запишутся следующим образом

В численном анализе показано, что если F дается формулами, то более точные приближения достигаются при интерполяции рациональными функциями.

Алгоритм рациональной экстраполяции, основанный на интерполяции рациональными функциями, разработан Булиршем и Штёром и имеет следующий вид:

Элементы данной таблицы при j = 2 вычисляются следующим образом:

Величины R^[j] можно представить с помощью рациональных функций следующего вида:

то есть функциями:

2 Метод Грэгга - Булирша - Штера

Для того чтобы применять локальную экстраполяцию к решению обыкновенных дифференциальных уравнений, необходимо использовать в качестве основы интерполяции численный метод, для которого справедливо асимптотическое разложение вида

Грэгг показал, что метод экстраполяции разложений вида нельзя основывать, например, на методе трапеций, так как разложение вида справедливо только тогда, когда разностные уравнения решаются точно. По этой же причине метод нельзя также основывать на неявных симметричных методах.

В методе рациональной экстраполяции Булирш и Штер используют модифицированный метод прямоугольников. Наиболее распространенный алгоритм экстраполяции Булирша - Штера основан на простейшем симметричном многошаговом методе прямоугольников

При этом симметрия сохраняется, если в качестве приближения к y(x) берется y(X;h) = y_N, или

Дополнительное начальное значение y₁ задается формулой приближения

В качестве {h_i} рекомендуется выбирать последовательность чисел вида.

Этот модифицированный метод прямоугольников называется методом экстраполяции Грэгга - Булирша – Штера (или методом GBS). Метод GBS эквивалентен методу Рунге Кутты, если основная длина шага h_N и порядок экстраполяции фиксированы.

3 Метод Ромберга

Найдем с помощью квадратурной формулы трапеций приближенное значение интеграла, применив экстраполяцию Ричардсона (данный метод называется методом Ромберга):

Рисунок 2. График функции

В нижеследующей таблице представлены результаты работы программы:

r	Исходная формула	Экстраполированная формула	Точное значение	Погрешность вычислений	Погрешность формулы
2	3.98277278	4.04665506	4.04718956	0.0005345	0.00275556
4	4.03068449	4.04714980	4.04718956	0.00003976	0.00017222
8	4.04303347	4.04718692	4.04718956	0.00000264	0.00001076
16	4.04614856	4.04718939	4.04718956	0.00000017	0.00000067
32	4.04692918	4.04718955	4.04718956	0.00000001	0.00000004
64	4.04712446	4.04718956	4.04718956	0	0
20384	4.04718956

Здесь r - коэффициент измельчения шага h. Исходная величина шага равна 2.

На рисунке черная сплошная линия - исходная формула, красная пунктирная - экстраполированная.

Как мы видим, разница между экстраполированными и неэкстраполированными результатами значительна. Уже при величине шага в  мы можем найти значение интеграла с точностью , тогда как в исходной формуле нам для достижения такой точности пришлось бы задать величину шага .

Заключение

В данном реферате была расмотрена экстраполяция Ричардсон, а также следующие из нее методы ГБШ и Ромберга. Достоинство методов экстраполяции заключается прежде всего в том, что при их использовании не требуется многократного перевычисления правых частей дифференциальных уравнений. Это особенно важно, когда правые части уравнений достаточно сложны.

Список источников

1. Сальвадори, М. Жд. Численные методы в технике / М. Дж. Сальвадори. М.: издательство иностранной литературы, 1955. 245.

2. Заусаев А. Ф. Разностные методы решения обыкновенных дифференциальных уравнений / А. Ф. Заусаев. Учеб. пособие Самара: Самарский гос. техн. ун-т, 2010. 100 с.

3. Рукавишников, А. В. Метод конечных разностей: учеб. пособие / А.В. Рукавишников, В. А. Рукавишников. Хабаровск: Изд-во ДВГУПС, 2012. 83 с.