Int I; // I - счетчик членов ряда

double res=1.0, // значение експоненты

X, // аргумент функции

eps, // задаваемая точность вычислений

member; // очередной член ряда

printf ("Input value of argument:");

scanf("%lf",&x);

printf ("\nInput precision:");

scanf("%lf",&eps);

for (i=2, member=x; fabs(member)>eps; i++) // проверка точности

{

res = res + member; // добавление в сумму нового члена ряда

member = member*x/i; // вычисление следующего члена ряда

}

printf ("\ny= %.40lf\nprecision: %.40lf\n",res,member);

printf ("number of series members: %u\n",i);

getch();

}

5. Методы нахождения корней уравнения: половинного деления, хорд, касательных, простой итерации.

Пусть задано уравнение вида f(x)=0,и известно, что на отрезке[a,b]оно имеет один корень, т.е. в точкахaиbзначения функции имеют разные знаки.

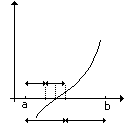
Если |a-b|<ε, где ε – требуемая точность вычислений, то любое значениеxиз заданного интервала (например,a) можно считать искомым корнем. Иначе в качестве приближения корня возьмем середину отрезкаx_i=(a+b)/2. Если значение функцииf(x_i)=0, то решение найдено. Иначе выбираем тот из отрезков([a,x_i],[x_i,b]), на концах которого значения функций имеют разные знаки, и следующий шаг алгоритма реализуем относительно этого отрезка.

Указанный алгоритм известен в литературе как метод половинного деления.

Заменим теперь исходное уравнение f(x)=0на равносильное ему уравнение вида x=φ(x). Пусть на отрезке[a,b]оно содержит только один корень. Выберем в качестве первого приближения некотороеx_i. Последующие приближения получаем по формуле x_i+1=φ(x_i). Если данная последовательность сходится, то она сходится к корню уравнения.

Описанный алгоритм носит название метода простой итерации.

Пусть функция имеет на отрезке один корень. Точки AиBимеют координатыA(a,f(a))иB(b,f(b). Искомым корнем будет абсциссаcточки пересечения графика сOx. Вместо нее ищется точка пересечения хордыABсOx.

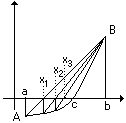
Уравнение прямой, проходящей через точки AиB, записывается в виде:

Первое приближение x₁ получаем подстановкойy=0:

илиили

Последующие приближения будем вычислять по формулам

При этом, если f(x_i)*f(b)<0(т.е.f(x_i)иf(b)разных знаков) то последующие приближения вычисляются по формуле (1), иначе – по формуле (2).

Если на отрезке [a,b]существует первая и вторая производные указанной функции, сохраняющие постоянный знак, то последовательностьx_iмонотонно сходится к корню уравненияf(x)=0.

Рассмотренный алгоритм представляет известный метод хорд.

Немного иначе устроен метод касательных. В этом случае приближение осуществляется на основе замены дуги касательной, проведенной к одной из крайних точек.

Итерационная формула описывается как:

Если на отрезке [a,b] f’(x)*f’’(x)>0, то нулевое приближение корня – это значениеx₀=b, иначеx₀=a.

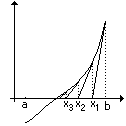
Пусть у нас задана функция y=x²-3.Приx=1 – y=-2, а приx=2 – y=1. Это как раз наш случай – на интервале [1,2] – есть корень. Программа, реализующая поиск корня по методу касательных, может выглядеть так:

#include <stdio.h>

#include <math.h>

#include <conio.h>

//////////////////////// Вычисление функции

double func(double x) { return (x*x - 3.0); }

//////////////////////// Вычисление производной функции

double derfunc(double x) { return (2*x); }

////////////////////////////////// Реализация метода касательных