6.4. Выбор шага интегрирования для равномерной сетки

Данная задача состоит в выборе шага h, обеспечивающего заданную точностьвычисления интеграла по выбранной формуле численного интегрирования.

Известны два подхода к решению данной задачи:

1) выбор шага по теоретическим оценкам погрешностей (23);

2) по косвенным схемам (эмпирическим оценкам).

6.4.1. Выбор шага интегрирования по теоретическим оценкам погрешностей

Пусть требуется вычислить интеграл с точностью . Тогда, используя формулу дляR, выбирают шаг так, чтобы

| R | </2 .

Учитывается также число знаков после запятой, чтобы погрешность округления не превышала /2.

Пример. С помощью формулы Симпсона вычислитьс точностью= 10^–3.

Решение. Выберем шагh.

;   [a,b], т.е.   [/4,/2] ;

Согласно соотношений (23), получим

< 0,510^–3.

Вычислим f ^IV(x)

. (24)

Оценим | f ^IV| на отрезке [/4,/2]. Воспользуемся величинами из (24)и. Они положительные и убывают, следовательно, их максимальное значение в точкеx=/4.

При этом +< 81. Таким образом,< 0,510^–3;h⁴ < 1410^–4;h 0,19.

С другой стороны для данного метода hвыбирается с учетом того, чтобы [/4,/2] делился на четное число отрезков. Этим двум требованиям отвечаетh=/24 = 0,13 < 0,19, при которомn = = 6. Тогда, чтобы погрешность округления не превысила 0,510^–3достаточно вычисления выполнить с 4 знаками после запятой.

Составим таблицу , сh=/24 = 730´ = 0,1309

i	xi0	xi	sin x	y0, y6	y2m	y2m–1
0	45 00´	0,7854	0,7071	0,9003
1	52 30´	0,9163	0,7934			0,8659
2	60 00´	1,0472	0,8660		0,8270
3	67 30´	1,1781	0,9239			0,7843
4	75 00´	1,3090	0,9659		0,7379
5	82 30´	1,4399	0,9914			0,6885
6	90 00´	1,5708	1,0000	0,6366
Сумма				1,5369	1,5649	2,3386

Для n= 6 по формуле Симпсона

.

6.4.2. Выбор шага интегрирования по эмпирическим схемам

1. Двойной пересчет

В связи с тем, что вычисления максимального значения по абсолютной величине k-ой производной приводят к громоздкости расчетов, на практике прибегают к искусственным приемам достижения заданной точности. А именно, определенный интеграл вычисляют по какой-либо квадратурной формуле дважды с шагомhиh/2, что удваивает числоn.

Определяют:

если | I_n–I_2n| <, тоI=I_2n;

если | I_n–I_2n| >, то берут шагh/4; (25)

если | I_2n – I_4n | <  , то I = I_4n .

В качестве начального шага hможно рекомендоватьh=, гдеm=2 для формул среднего и трапеций,m=4 – для Симпсона.

2. Схема Эйткина

На практике для повышения точности численного интегрирования широко используется схема Эйткина. Рассмотрим ее смысл.

Расчет проводиться три раза с h₁,h₂,h₃, при этом соотношение между ними. Получают три значенияI₁,I₂,I₃.

Производится уточнение по эмпирической формуле:

. (26)

Порядок точности =.

3. Правило Рунге

Это наиболее популярное практическое правило, разработанное в предположении, что f(x)C⁴[a,b] для квадратурных формул прямоугольников и трапеций,f(x)C⁶[a,b] – для формулы Симпсона. В этом случае можно показать, что погрешностиR(h,f) имеют следующие представления приh0:

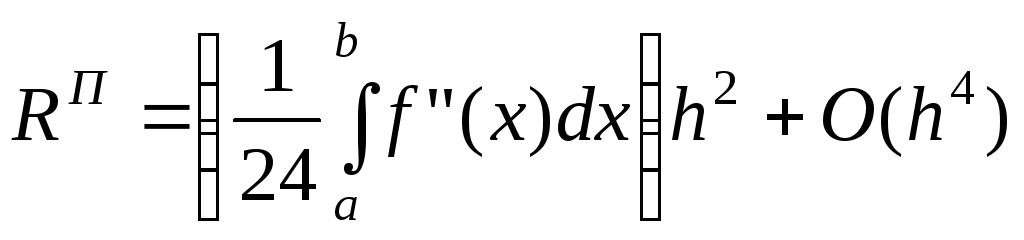; (27)

;

.

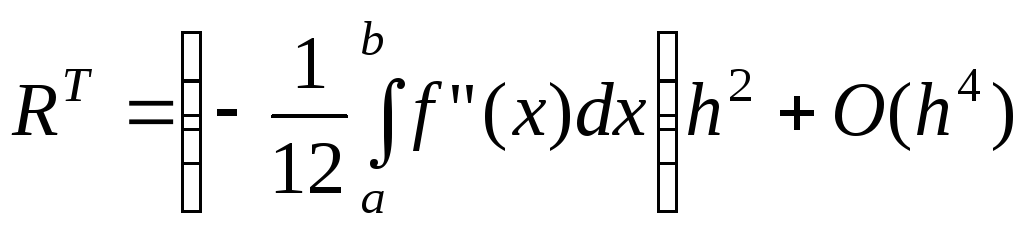Суть его также состоит в том, чтобы, организовав вычисления двух значений интеграла по двум семействам узлов, сравнивают результаты вычислений с оценкой погрешности. Объединив (27) можно получить рабочую формулу:

; (28)

где k= 2,m= 2 – для прямоугольников и трапеций;

k= 4,m= 2 – для формулы Симпсона.