
11 Погрешности измерений
.pdf
iZ TABLICY 3.1 WIDNO, ^TO TOLXKO PRI n = 60 POLU^IM DOWERITELXNU@ WEROQTNOSTX ® = 0;7. |TO | NEWYSOKAQ NADEVNOSTX IZMERENIJ. uWELI^ITX NADEVNOSTX IZMERENIJ PRO]E UWELI^ENIEM DOWERITELXNOGO INTERWALA. oBY^NO PRINIMA@T ¾(x) = 2¾ (hxi) ILI DAVE ¾(x) = 3¾ (hxi). mETODOM PROPORCIONALXNOGO S^ETA (SM. TABL. 3.1) MOVNO POLU^ITX, ^TO PRI n = 5 | 7 : ESLI ¾(x) = ¾ (hxi), TO ® = 0;62,
ESLI ¾(x) = 2¾ (hxi) TO ® = 0;9, ESLI ¾(x) = 3¾ (hxi) TO ® = 0;96. oBY^NO IZMERENIQ, NE TREBU@]IE BOLX[OJ TO^NOSTI, PROWODQT S NADEVNOSTX@ (DOWERITELXNOJ WEROQTNOSTX@) ® = 0;9.
tABLICA 3.1 { kO\FFICIENTY sTX@DENTA, t.
|
|
|
dOWERITELXNAQ WEROQTNOSTX, ® |
|
|
|||||
n |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,98 |
|
0,99 |
0,999 |
2 |
1,0 |
1,38 |
2,0 |
3,1 |
6,3 |
12,7 |
31,8 |
|
63,7 |
636,6 |
3 |
0,82 |
1,06 |
1,3 |
1,9 |
2,9 |
4,3 |
7,0 |
|
9,9 |
31,6 |
4 |
0,77 |
0,98 |
1,3 |
1,6 |
2,4 |
3,2 |
4,5 |
|
5,8 |
12,9 |
5 |
0,74 |
0,94 |
1,2 |
1,5 |
2,1 |
2,8 |
3,7 |
|
4,6 |
8,7 |
6 |
0,73 |
0,92 |
1,2 |
1,5 |
2,0 |
2,6 |
3,4 |
|
4,0 |
6,9 |
7 |
0,72 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,1 |
|
3,7 |
6,0 |
8 |
0,71 |
0,90 |
1,1 |
1,4 |
1,9 |
2,4 |
3,0 |
|
3,5 |
5,4 |
9 |
0,71 |
0,89 |
1,1 |
1,4 |
1,8 |
2,3 |
2,9 |
|
3,4 |
5,0 |
10 |
0,70 |
0,88 |
1,1 |
1,4 |
1,8 |
2,3 |
2,8 |
|
3,3 |
4,8 |
15 |
0,69 |
0,87 |
1,1 |
1,3 |
1,8 |
2,1 |
2,6 |
|
3,0 |
4,1 |
20 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
|
2,9 |
3,9 |
25 |
0,69 |
0,86 |
1,1 |
1,3 |
1,7 |
2,1 |
2,5 |
|
2,8 |
3,7 |
30 |
0,68 |
0,85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,5 |
|
2,8 |
3,7 |
40 |
0,68 |
0,85 |
1,1 |
1,3 |
1,7 |
2,0 |
2,4 |
|
2,7 |
3,6 |
60 |
0,68 |
0,85 |
1,0 |
1,3 |
1,7 |
2,0 |
2,4 |
|
2,7 |
3,5 |
120 |
0,68 |
0,84 |
1,0 |
1,3 |
1,7 |
2,0 |
2,4 |
|
2,6 |
3,4 |
3.3 oCENKA SUMMARNOJ POGRE[NOSTI PRQMYH IZMERENIJ
eSLI ODNA IZ POGRE[NOSTEJ (SISTEMATI^ESKAQ ILI SLU^AJNAQ) MENX[E DRUGOJ W TRI I BOLEE RAZ, TO EE MOVNO NE U^ITYWATX. o[IBKA W OCENKE SUMMARNOJ POGRE[NOSTI NE PREWYSIT PRI \TOM 10%. eSLI VE SISTEMATI^ESKAQ POGRE[NOSTX I SLU^AJNAQ BLIZKI DRUG K DRUGU, TO ONI W ODINAKOWOJ STEPENI OPREDELQ@T TO^NOSTX REZULXTATA I NUVNO U^ITYWATX OBE POGRE[NOSTI. k SOVALENI@, DOSTATO^NO STROGOGO PRAWILA OPREDELENIQ SUMMARNOJ POGRE[NOSTI NET.
tIPI^NYJ METOD OPREDELENIQ SUMMARNOJ POGRE[NOSTI SOSTOIT W SLEDU@]EM. sISTEMATI^ESKAQ POGRE[NOSTX S^ITAETSQ TOVE SLU^AJNOJ WELI^INOJ I, TAK KAK ONA ESTX MAKSIMALXNAQ POGRE[NOSTX DANNOGO PRIBORA, EJ PRIPISYWAETSQ DOWERITELXNAQ WEROQTNOSTX ® = 0;997

(IMENNO TAKOE ZNA^ENIE ® PODTWERVDENO MNOGO^ISLENNYMI \KSPERIMENTAMI). tOGDA, IZ TEORII WEROQTNOSTEJ SLEDUET, ^TO SUMMARNAQ ABSOL@TNAQ POGRE[NOSTX IZMERENIJ
q
¾(x)§ = ¾2(x)SIST. + [3¾ (hxi)]2; (3.7)
S DOWERITELXNOJ WEROQTNOSTX@ ® = 0;96 (PRI n = 5 | 7 IZMERENIQH). w LABORATORNOM PRAKTIKUME MOVNO POLXZOWATXSQ I UPRO]ENNOJ
FORMULOJ :
¾(x)§ = ¾(x)SIST. + 2¾ (hxi) : |
(3.8) |
dOWERITELXNAQ WEROQTNOSTX W \TOM SLU^AE PRI n = 5 | 7 RAWNA
® = 0;95.
iTAK, ESLI W REZULXTATE MNOGOKRATNYH IZMERENIJ KAKOJ-LIBO WELI^INY POLU^EN RQD SOWER[ENNO ODINAKOWYH ZNA^ENIJ, TO W \TOM SLU^AE SLU^AJNAQ POGRE[NOSTX SU]ESTWENNO MENX[E (ONA ESTX !) SISTEMATI^ESKOJ I EE NEWOZMOVNO U^ESTX. eSLI REZULXTATY IZMERENIJ OTLI^A@TSQ ODIN OT DRUGOGO, TO W \TOM SLU^AE NEOBHODIMO OCENITX KAK SISTEMATI^ESKU@, TAK I SLU^AJNU@ POGRE[NOSTI I NAJTI IH SUMMU.
fORMULY (3.7) I (3.8) MOVNO ISPOLXZOWATX I DLQ NAHOVDENIQ SUMMARNYH OTNOSITELXNYH POGRE[NOSTEJ :
"(x)§ = q |
|
; |
|
"2(x)SIST. + [3" (hxi)]2 |
(3.9) |
||
"(x)§ = "(x)SIST. + 2" (hxi) : |
(3.10) |
||
4 oCENKA POGRE[NOSTI KOSWENNYH IZMERENIJ
pUSTX ISKOMAQ WELI^INA QWLQETSQ FUNKCIEJ NESKOLXKIH ARGUMENTOW, KOTORYE NAHODQTSQ W REZULXTATE PRQMYH IZMERENIJ :
y = f(x1; x2; : : : ; xi; : : : ; xk);
GDE k | ^ISLO ARGUMENTOW, QWLQ@]IHSQ REZULXTATOM PRQMYH IZMERENIJ.
aBSOL@TNAQ POGRE[NOSTX KOSWENNOGO IZMERENIQ |
|
||||||
|
|
|
|
|
|
|
|
uX· |
@y ¾(xi)§ |
¸ |
2 |
; |
(4.1) |
||
¾(y)§ = v k |
|
||||||
t |
|
|
|
|
|
|
|
ui=1 |
@xi |
|
|
|
|
||
GDE ¾(xi)§ | ABSOL@TNAQ SUMMARNAQ POGRE[NOSTX xi-GO ARGUMENTA.

oTNOSITELXNAQ POGRE[NOSTX KOSWENNOGO IZMERENIQ |
|
||||||
|
|
|
|
|
|
|
|
uX· |
@ ln y ¾(xi)§ |
¸ |
2 |
; |
(4.2) |
||
"(y)§ = v k |
|
||||||
t |
|
|
|
|
|
|
|
ui=1 |
@xi |
|
|
|
|
||
dOWERITELXNAQ WEROQTNOSTX NAJDENNYH ZNA^ENIJ ¾(y) I "(y) RAWNA DOWERITELXNOJ WEROQTNOSTI ¾(x)§, PO\TOMU NEOBHODIMO, ^TOBY DOWERITELXNYE WEROQTNOSTI ARGUMENTOW BYLI RAWNY DRUG DRUGU. pRIMER POLXZOWANIQ FORMULAMI (4.1) I (4.2) NAHODITSQ W RAZDELE 6. tEM, KTO NE ZNAKOM S DIFFERENCIALXNYM IS^ISLENIEM I S ^ASTNYMI PROIZWODNYMI, MOVNO NA PERWYH PORAH POLXZOWATXSQ PROSTYMI PRAWILAMI, WYTEKA@]IMI IZ FORMUL (4.1) I (4.2), SM. TABLICU 4.1.
sLEDUET UKAZATX, ^TO SLU^AJNU@ POGRE[NOSTX KOSWENNOGO IZMERENIQ MOVNO NAJTI KAK SREDNEKWADRATI^NU@ POGRE[NOSTX SREDNEGO ARIFMETI^ESKOGO IZ NESKOLXKIH REZULXTATOW KOSWENNYH IZMERENIJ WELI^INY y. w SOOTWETSTWII S FORMULOJ (3.5) :
|
|
n |
|
|
|
|
|
vi=1(yi ¡ hyi)2 |
|
|
|||
¾ ( y |
) = u |
P |
|
|
: |
(4.3) |
n(n |
|
1) |
||||
h i |
u |
|
|
|
||
|
u |
|
|
|
|
|
|
t |
|
¡ |
|
|
|
tABLICA 4.1 { pROSTEJ[IE FORMULY DLQ NAHOVDENIQ POGRE[NOSTI KOSWENNOGO IZMERENIQ.
fUNKCIQ |
|
|
|
fORMULA DLQ RAS^<TA POGRE[NOSTI |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = x1 § x2 |
|
|
2 |
¾2 |
x |
2) |
|
|
|
|
||||||||||||
|
|
¾(y) = p |
¾ |
(x1) + |
|
( |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ILI |
|
|
2 |
2 |
|
x |
|
|
|
|
|
|
|||||
y = x1 ¢ x2 |
y = x1 |
=x2 |
"(y) = p |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
" (x1) + " ( 2) |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
x1 |
|
x2 |
|
xn |
|
"(y) = s 1 |
|
|
|
|
|
|
|
|
|
|
|||||
y = |
z1 |
¢ z2 |
¢ ¢ ¢ ¢ ¢zm |
|
"2(xi) + |
|
1 |
"2(zi) |
||||||||||||||
|
|
|
¢ |
|
¢ ¢ ¢ ¢ ¢ |
|
|
|
|
|
P |
|
P |
|
|
|
|
|
|
|||
y = xm |
|
|
|
|
|
"(y) = m"(x) |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = px |
|
|
|
"(y) = |
m |
"(x) |
|
|
|
|
|
|
|
|
|
|||||||
y = ln x |
|
|
|
¾(y) = "(x) ; "(y) = |
|
"(x) |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
j ln xj |
||||||||||||||||||
y = lg x |
|
|
|
¾(y) = |
"(x) |
; "(y) = |
|
|
|
"(x) |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
ln 10 |
ln 10 ¢ j ln xj |
||||||||||||||||||

5 tO^NOSTX WY^ISLENIJ I ZAPISX REZULXTATA IZMERENIJ
tO^NOSTX OBRABOTKI ^ISLOWOGO MATERIALA DOLVNA BYTX SOGLASOWANA S TO^NOSTX@ SAMIH IZMERENIJ. wY^ISLENIQ, PROIZWEDENNYE c BOLX[IM ^ISLOM DESQTI^NYH ZNAKOW, ^EM \TO NEOBHODIMO, SOZDA@T LOVNOE WPE^ATLENIE O BOLX[OJ TO^NOSTI IZMERENIJ. w TO VE WREMQ, RAZUMEETSQ, NE SLEDUET UHUD[ATX REZULXTATY IZMERENIJ, POLXZUQSX IZLI[NE GRUBYMI METODAMI WY^ISLENIQ.
|KSPERIMENTATORY PRIDERVIWA@TSQ PROSTOGO PRAWILA : POGRE[- NOSTX, POLU^A@]AQSQ W REZULXTATE WY^ISLENIJ, DOLVNA BYTX PRIMERNO NA PORQDOK, T.E. W DESQTX RAZ, MENX[E SUMMARNOJ POGRE[NOSTI IZMERENIJ. pRI \TOM MOVNO BYTX UWERENNYM, ^TO W PROCESSE ARIFMETI^ESKIH WY^ISLENIJ O]UTIMYM OBRAZOM NE ISKAZQTSQ REZULXTATY IZMERENIJ.
pRI DESQTI I MENX[EM ^ISLE IZMERENIJ PRIDERVIWA@TSQ SLEDU- @]EGO PRAWILA. pRI ZAPISI SUMMARNOJ WELI^INY POGRE[NOSTI PRIWODQT ODNU ZNA^A]U@ CIFRU, ESLI ONA BOLX[E TREH, I DWE ZNA^A- ]IE CIFRY, ESLI PERWAQ IZ NIH MENX[E ^ETYREH. nAPRIMER, ESLI
¾(x) = 0;423, TO ZAPISYWA@T ¾(x) = 0;4 ; ESLI ¾(x) = 0;324, TO SLEDU-
ET PISATX DWE ZNA^A]IE CIFRY ¾(x) = 0;32. pOSKOLXKU POGRE[NOSTX ZAPISYWA@T, ISPOLXZUQ MAKSIMUM DWE CIFRY, TO ARIFMETI^ESKIE WY- ^ISLENIQ SLEDUET PROWODITX, ISPOLXZUQ MAKSIMUM TRI ZNA^A]IE CIFRY.
pRI ZAPISI REZULXTATA IZMERENIJ, T.E. WELI^INY hxi, POSLEDNEJ ZNA^A]EJ CIFROJ SLEDUET UKAZYWATX TU, RAZRQD KOTOROJ SOOTWETSTWUET MLAD[EMU RAZRQDU POGRE[NOSTI IZMERENIJ. nAPRIMER, NA- [LI, ^TO SOPROTIWLENIE PROWODNIKA hRi = 28;735 oM, POGRE[NOSTX IZMERENIQ PRI \TOM ¾(R) = 0;247 oM. oTWET SLEDUET ZAPISATX TAK :
R = (28;73 § 0;25) oM:
eSLI BY POGRE[NOSTX IZMERENIQ OKAZALASX DRUGOJ, NAPRIMER,
¾(R) = 0;438 oM, TO
R = (28;7 § 0;4) oM:
6 pRIMER OCENKI POGRE[NOSTI KOSWENNOGO IZMERENIQ
pUSTX PRI IZMERENII SOPROTIWLENIQ NEKOEGO REZISTORA ISPOLXZU- @TSQ SLEDU@]IE PRIBORY : WOLXTMETR KLASSA TO^NOSTI 1;0 S MAKSI-
MALXNYM ZNA^ENIEM [KALY 50 w I AMPERMETR KLASSA TO^NOSTI 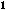
co [KALOJ 75 Ma. dLQ OPREDELENIQ R MOVNO WOSPOLXZOWATXSQ ZAKONOM
oMA :
R = U=I:

rEZULXTATY PQTI IZMERENIJ NAPRQVENIQ U I TOKA I PRIWEDENY W TABLICE 6.1.
tABLICA 6.1
iZMERQEMAQ |
|
|
|
|
|
|
|
|
|
|
|
|
||
WELI^INA |
|
|
1 |
|
2 |
|
3 |
|
4 |
5 |
6 |
|||
U, w |
|
|
|
25,5 |
|
25,0 |
|
24,7 |
|
25,3 |
24,5 |
25,0 |
||
I, Ma |
|
|
|
50,5 |
|
50,0 |
|
49,5 |
|
50,5 |
50,5 |
50,2 |
||
h |
R |
i |
= |
hUi |
= |
|
25;0 |
= 497 oM: |
|
|||||
|
|
|
|
|||||||||||
|
|
|
hIi |
50;2 ¢ 10¡3 |
|
|
|
|
||||||
oCENIM POGRE[NOSTX NAJDENNOJ WELI^INY hRi. w DANNOM SLU^AE PRO]E NAJTI OTNOSITELXNU@ POGRE[NOSTX. iZ TABLICY 4.1 SLEDUET,
^TO
p
"(R)§ = "2(U)§ + "2(I)§: |
(6.1) |
iTAK, NUVNO NAJTI SUMMARNYE OTNOSITELXNYE POGRE[NOSTI IZMERENIJ "(U)§ I "(I)§. tAK KAK KLASS TO^NOSTI WOLXTMETRA 1;0 , TO EGO ABSOL@TNAQ SISTEMATI^ESKAQ POGRE[NOSTX, W SOOTWETSTWII S FORMU-
LOJ (3.2) :
¾(U)SIST. = |
50 ¢ 1;0% |
= 0;5 w; |
"(U)SIST. = |
|
0;5 |
= 0;02: |
|
25;0 |
|||||||
|
100% |
|
|
|
|||
kLASS TO^NOSTI AMPERMETRA 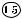 | \TO ZNA^IT, ^TO OTNOSITELX-
| \TO ZNA^IT, ^TO OTNOSITELX-
NAQ POGRE[NOSTX "(I)SIST. = 0;015.
sREDNQQ KWADRATI^NAQ POGRE[NOSTX hUi (SLU^AJNAQ), W SOOTWETSTWII S FORMULOJ (3.5), RAWNA :
¾(hUi) = r |
|
|
|
|
|
0;52 + 02 + 0;32 + 0;32 + 0;52 |
|
= 0;184 w: |
|
5 4 |
|
|||
|
¢ |
|
|
|
oTNOSITELXNAQ SLU^AJNAQ POGRE[NOSTX IZMERENIQ hUi
"(hUi) = 0;184 = 0;74 ¢ 10¡2: 25;0
sUMMARNAQ POGRE[NOSTX hUi S DOWERITELXNOJ WEROQTNOSTX@ ® = 0;96 BUDET RAWNA W SOOTWETSTWII S FORMULOJ (3.9) :
q
"(hUi)§ = (2 ¢ 10¡2)2 + (3 ¢ 0;74 ¢ 10¡2)2 = 3 ¢ 10¡2 = 3%:

sREDNQQ KWADRATI^NAQ ABSOL@TNAQ POGRE[NOSTX WELI^INY hIi RAW-
NA :
r
¾(hIi) = |
0;32 + 0;22 + 0;72 + 0;32 + 0;32 |
= 0;2 Ma: |
|||||
|
|
5 |
¢ |
4 |
|
||
|
|
|
|
|
|
|
|
oTNOSITELXNAQ SLU^AJNAQ POGRE[NOSTX |
|
|
|||||
"(hIi) = |
0;2 |
= 0;397 |
¢ 10¡2 = 0;4 |
¢ 10¡2: |
|||
|
|||||||
50;2 |
|||||||
3 ¢ "(hIi) = 3 ¢ 0;004 = 0;012 | SLU^AJNAQ I SISTEMATI^ESKAQ POGRE[- NOSTI PRI IZMERENII I PRIMERNO RAWNY, PO\TOMU IH NUVNO SKLADY-
WATX :
q
"(hIi)§ = (1;5 ¢ 10¡2)2 + (3 ¢ 1;2 ¢ 10¡2)2 = 1;9 ¢ 10¡2:
sUMMARNAQ OTNOSITELXNAQ POGRE[NOSTX IZMERENIQ WELI^INY hRi : q
"(hRi)§ = (3 ¢ 10¡2)2 + (1;9 ¢ 10¡2)2 = 3;56 ¢ 10¡2: aBSOL@TNAQ SUMMARNAQ POGRE[NOSTX hRi :
¾(hRi)§ = hRi ¢ "(hRi)§ = 497 ¢ 3;56 ¢ 10¡2 = 17;7 oM:
oKON^ATELXNO, S DOWERITELXNOJ WEROQTNOSTX@ ® = 0;96 MOVNO UTWERVDATX, ^TO ISKOMAQ WELI^INA
R = hRi § ¾(hRi)§ = 497 § 18 oM:
w RASSMATRIWAEMOM PRIMERE MOVNO BYLO POSTUPITX I PO DRUGOMU : SRAZU NAJTI SUMMARNU@ SLU^AJNU@ POGRE[NOSTX hRi. dLQ \TOGO NADO BYLO PQTX RAZ WY^ISLITX R PO DANNYM TABLICE 6.1 I NAJTI SREDNEKWADRATI^NU@ ABSOL@TNU@ POGRE[NOSTX ¾(hRi), ZATEM, NAJDQ ¾(R)SIST., SLOVITX ¾(R)SIST., I 3¾(hRi) PO FORMULE (3.7).
7 pOSTROENIE GRAFIKOW I OCENKA GRAFI^ESKIH POGRE[NOSTEJ
7.1 pOSTROENIE GRAFIKOW S ISPOLXZOWANIEM DOWERITELXNYH INTERWALOW
w PRAKTIKE NAU^NYH ISSLEDOWANIJ O^ENX ^ASTO PRIHODITSQ STROITX GRAFI^ESKIE ZAWISIMOSTI ODNOJ IZ IZMERQEMYH WELI^IN OT DRUGOJ. nALI^IE POGRE[NOSTEJ IZMERENIJ OBUSLOWLIWAET TOT FAKT, ^TO \KSPERIMENTALXNYE TO^KI NE TO^NO LOVATSQ NA PRQMU@ ILI KRIWU@, WYRAVA@]U@ TEORETI^ESKU@ ZAWISIMOSTX MEVDU \TIMI WELI^INAMI.
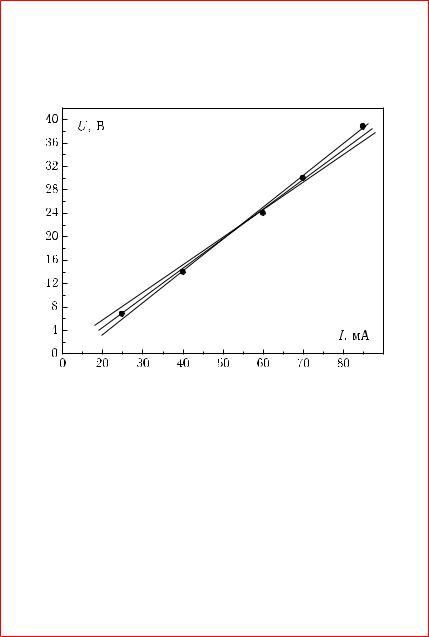
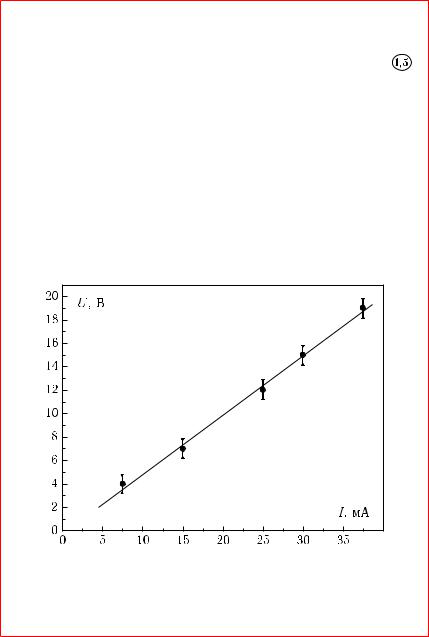
nAPRIMER, NA RISUNKE 7.1 POKAZANA \KSPERIMENTALXNAQ ZAWISIMOSTX NAPRQVENIQ NA NEIZWESTNOM SOPROTIWLENIE R OT WELI^INY PROTEKA@]EGO ^EREZ NEGO TOKA. |KSPERIMENTALXNYE TO^KI RASPOLOVILISX TAK, ^TO ODNOZNA^NO PROWESTI PRQMU@, WYRAVA@]U@ \TU ZAWISIMOSTX, ZATRUDNITELXNO : NA RISUNKE 7.1 POKAZANY TRI WOZMOVNYH WARIANTA ZAWISIMOSTI. kAKOJ IZ NIH WEREN ?
rISUNOK 7.1 { zAWISIMOSTX NAPRQVENIQ U NA SOPROTIWLENII OT TOKA I.
oDIN IZ [IROKO RASPROSTRANENNYH PRIBLIVENNYH METODOW PROWEDENIQ \KSPERIMENTALXNOJ ZAWISIMOSTI ZAKL@^AETSQ W TOM, ^TO NA GRAFIKE UKAZYWAETSQ DOWERITELXNYE INTERWALY ZNA^ENIJ IZMERENNYH WELI^IN. pRI POSTROENII DOWERITELXNOGO INTERWALA SLEDUET IMETX W WIDU DWE SITUACII :
1)KAVDAQ \KSPERIMENTALXNAQ TO^KA | REZULXTAT MNOGOKRATNOGO IZMERENIQ. w \TOM SLU^AE SLEDUET NAJTI SUMMARNYE ABSOL@TNYE POGRE[NOSTI KAVDOJ IZ IZMERENNYH WELI^IN (SM. PODRAZDELY 3.1 | 3.3) : ONI OTKLADYWA@TSQ PO OBE STORONY OT TO^KI NA GRAFIKE WDOLX SOOTWETSTWU@]IH KOORDINATNYH OSEJ. pRI \TOM MOVNO TO^NO UKAZATX DOWERITELXNU@ WEROQTNOSTX PROWEDENNYH IZMERENIJ ;
2)GORAZDO ^A]E WSTRE^A@]IJSQ SLU^AJ : KAVDAQ \KSPERIMENTALXNAQ TO^KA | REZULXTAT ODNOKRATNOGO IZMERENIQ. w \TOM SLU^AE MOVNO NAJTI TOLXKO ABSOL@TNYE SISTEMATI^ESKIE POGRE[NOSTI REZULXTATOW IZMERENIJ I TAKVE OTLOVITX PO OBE STORONY OT SOOTWETSTWU@- ]EJ \KSPERIMENTALXNOJ TO^KI. sLEDUET ZAMETITX, ^TO DLQ PRIBOROW,
U KOTORYH POSTOQNNOJ QWLQETSQ ABSOL@TNAQ POGRE[NOSTX (KLASS TO^- NOSTI TAKIH PRIBOROW OBOZNA^AETSQ, NAPRIMER, 1;0), OTREZKI DOWERITELXNYH INTERWALOW BUDUT ODINAKOWYMI ; ESLI IZMERENIQ PROWEDENY
S POMO]X@ PRIBOROW, KLASS TO^NOSTI KOTORYH OBOZNA^AETSQ |
, |
DOWERITELXNYE INTERWALY BUDUT NEODINAKOWYMI. |
|
w KA^ESTWE PRIMERA RASSMOTRIM E]E ODIN METOD IZMERENIQ SOPROTIWLENIQ, | PRI KOTOROM NE STARA@TSQ USTANOWITX ODNO I TO VE ZNA^ENIE NAPRQVENIQ, KAK W RAZDELE 6, A IZMERQETSQ TOK PRI ZAWEDOMO RAZNYH NAPRQVENIQH. kAVDOE IZ \TIH IZMERENIJ PROWODITSQ ODIN RAZ. pOLOVIM, ^TO SOPROTIWLENIE I PRIBORY IME@T TE VE HARAKTERISTIKI, ^TO I W RAZDELE 6. rEZULXTATY IZMERENIJ PREDSTAWLENY W TABLICE 7.1.
tABLICA 7.1 { rEZULXTATY IZMERENIJ TOKA I NAPRQVENIQ
I, Ma |
7,5 |
15 |
25 |
30 |
37,5 |
U, w |
4 |
7 |
12 |
15 |
19 |
pO REZULXTATAM IZMERENIJ POSTROEN GRAFIK (RISUNOK 7.2).
rISUNOK 7.2 { sWQZX MEVDU TOKOM I I NAPRQVENIEM U DLQ POSTOQNNOGO SOPROTIWLENIQ.
|KSPERIMENTALXNYE TO^KI NE STROGO UKLADYWA@TSQ NA PRQMU@ I, ^TOBY PROWESTI \TU PRQMU@ BOLEE TO^NO, POSTROIM DOWERITELXNYE INTERWALY. tAK KAK IZMERENIQ ODNOKRATNYE, TO DOWERITELXNYE

INTERWALY BUDUT PREDSTAWLQTX SOBOJ ABSOL@TNYE POGRE[NOSTI PRIBOROW, S POMO]X@ KOTORYH PROWODILISX IZMERENIQ TOKA I NAPRQVENIQ. pRI KLASSE TO^NOSTI WOLXTMETRA 1;0 I MAKSIMALXNOM ZNA^ENII [KALY PRIBORA 50 w ABSOL@TNAQ POGRE[NOSTX RAWNA 0;5 w. pARALLELXNO OSI NAPRQVENIQ WWERH I WNIZ OT KAVDOJ \KSPERIMENTALXNOJ TO^KI NADO OTLOVITX 0;5 w W MAS[TABE GRAFIKA (RISUNOK 7.2).
u MILLIAMPERMETRA (KLASS TO^NOSTI 
 ) ABSOL@TNAQ POGRE[- NOSTX IZMENQETSQ, ^EM BOLX[E WELI^INA TOKA, TEM BOLX[E POGRE[- NOSTX. mAKSIMALXNAQ WELI^INA ABSOL@TNOJ POGRE[NOSTI IZMERENIQ TOKA BUDET RAWNA : ¾(I) = 37;5 ¢ 0;015 = 0;56 Ma. w MAS[TABE RISUNKA 7.2 \TO SOOTWETSTWUET PRIMERNO 1;1 MM. dLQ DRUGIH \KSPERIMENTALXNYH TO^EK \RAZMER" DOWERITELXNOGO INTERWALA NA GRAFIKE BUDET E]E MENX[E. tAKIE MALYE INTERWALY NA GRAFIKAH OBY^NO NE OTKLADYWA@TSQ.
) ABSOL@TNAQ POGRE[- NOSTX IZMENQETSQ, ^EM BOLX[E WELI^INA TOKA, TEM BOLX[E POGRE[- NOSTX. mAKSIMALXNAQ WELI^INA ABSOL@TNOJ POGRE[NOSTI IZMERENIQ TOKA BUDET RAWNA : ¾(I) = 37;5 ¢ 0;015 = 0;56 Ma. w MAS[TABE RISUNKA 7.2 \TO SOOTWETSTWUET PRIMERNO 1;1 MM. dLQ DRUGIH \KSPERIMENTALXNYH TO^EK \RAZMER" DOWERITELXNOGO INTERWALA NA GRAFIKE BUDET E]E MENX[E. tAKIE MALYE INTERWALY NA GRAFIKAH OBY^NO NE OTKLADYWA@TSQ.
pRQMU@ SLEDUET PROWESTI TAK, ^TOBY ONA PRO[LA WNUTRI WSEH DOWERITELXNYH INTERWALOW. wO MNOGIH SLU^AQH OKAZYWAETSQ, ^TO PROWESTI PRQMU@ S SOBL@DENIEM \TOGO USLOWIQ WOZMOVNO EDINSTWENNYM OBRAZOM. pRI NAHOVDENII KAKOJ-LIBO WELI^INY x IZ GRAFIKA ABSO- L@TNAQ POGRE[NOSTX \TOJ WELI^INY ¾(x) OPREDELQETSQ TAK VE, KAK POGRE[NOSTX PRIBORA, NE IME@]EGO KLASSA TO^NOSTI : ¾(x) RAWNA POLOWINE CENY DELENIQ SOOTWETSTWU@]EJ [KALY GRAFIKA.
7.2 lINEARIZACIQ FUNKCIJ
w FIZI^ESKIH ISSLEDOWANIQH O^ENX ^ASTO DLQ SRAWNENIQ \KSPERIMENTA S TEORIEJ POLXZU@TSQ METODOM LINEARIZACII TEORETI^ESKOJ ZAWISIMOSTI. nAPRIMER, ISSLEDUETSQ ZAWISIMOSTX TOKA WAKUUMNOGO DIODA I OT WELI^INY ZADERVIWA@]EGO NAPRQVENIQ U MEVDU KATODOM I ANODOM. tEORETI^ESKAQ ZAWISIMOSTX IMEET SLEDU@]IJ WID :
eU |
¸; |
|
I = I0 exp ·¡kT |
(7.1) |
GDE I0 | TOK PRI U = 0 ; k | POSTOQNNAQ bOLXCMANA ; T | ABSOL@T- NAQ TEMPERATURA ; e | ZARQD \LEKTRONA.
pOSTROENNAQ PO \KSPERIMENTALXNYM DANNYM ZAWISIMOSTX I = f(U) MOVET S RAWNYM USPEHOM ILL@STRIROWATX I KWADRATI^NU@, I KUBI^ESKU@, I \KSPONENCIALXNU@ ZAWISIMOSTI. ~TOBY WYQSNITX, PODTWERVDA@T LI \KSPERIMENTALXNYE DANNYE TEORI@, TEORETI^ESKU@ ZAWISIMOSTX PREOBRAZU@T TAK, ^TOBY MEVDU FUNKCIEJ I I ARGUMENTOM U BYLA LINEJNAQ ZAWISIMOSTX.
pROLOGARIFMIROWAW WYRAVENIE (7.1), POLU^IM :
e |
|
|
ln I = ln I0 ¡ kT |
U: |
(7.2) |
|TO URAWNENIE PRQMOJ WIDA :
y = b ¡ ax; |
(7.3) |
|
GDE y = ln I ; b = ln I0 ; a = e |
| UGLOWOJ KO\FFICIENT |
PRQMOJ ; |
kT |
|
|
x = U. |
|
|
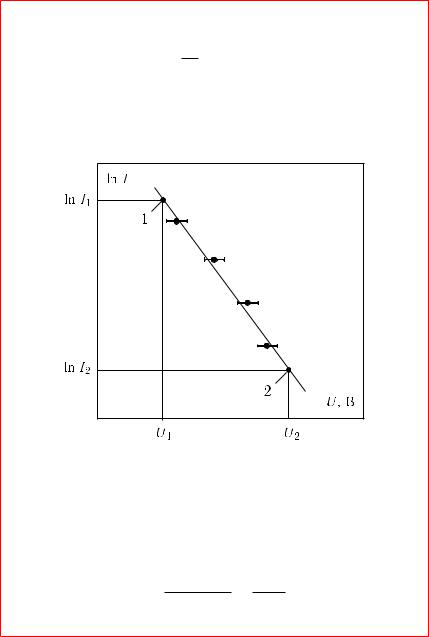
eSLI \KSPERIMENTALXNYE REZULXTATY ULQGUTSQ NA PRQMU@ (W PRE- |
||
DELAH POGRE[NOSTEJ IZMERENIJ) W KOORDINATAH ln I = f(U)), MOVNO |
||
UTWERVDATX, ^TO ZAWISIMOSTX MEVDU I I U NOSIT IMENNO \KSPONEN- |
||
CIALXNYJ HARAKTER, KAK \TO I SLEDUET IZ TEORII (RISUNOK 7.3). |
||
rISUNOK 7.3 { zAWISIMOSTX ln I OT WELI^INY ZADERVIWA@]EGO |
||
NAPRQVENIQ U. |
|
|
wO MNOGIH SLU^AQH ZNANIE UGLOWOGO KO\FFICIENTA a I WELI^I- NY b POZWOLQET OPREDELITX I DRUGIE PARAMETRY IZU^AEMOGO QWLENIQ. w DANNOM PRIMERE, ZNAQ a, MOVNO OPREDELITX TEMPERATURU KATODA. w PRIBLIV<NNYH WY^ISLENIQH UGLOWOJ KO\FFICIENT NAHODITSQ OBY^NO IZ GRAFIKA (RISUNOK 7.3) : TO^NO NA PRQMOJ WYBIRA@TSQ DWE TO^KI (1 I 2) I a OPREDELQETSQ KAK TANGENS UGLA NAKLONA PRQMOJ :
a = ln I2 ¡ ln I1 = ¢ ln I : ¢U
