Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

опред-интеграл-stud

.pdf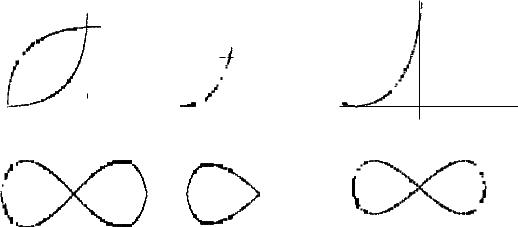

Скачиваний:

Добавлен:

11.05.2015

Размер:

636.3 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Решение . Фигура симметрична относительно осей координат и начала координат (рис. 11), поэтому найдем площадь части фигуры, расположенной в 1-ой четверти и умножим на 4.

cos3Rt =2

cos2 td(cos t) =

S = 4

3 sin 2t

4 cos tdt = 96

sin t cos2 tdt = 96

96 3

= 0 3 = 32.

6 ðèñ. 8

ðèñ. 9

ðèñ. 10

y = p

y = 2x + 12

y =

@ y = 8 x

(x + 6)2

y =

y = x3

6 y=3 sin 2t

6 r2 = a2 cos 2'

y=9t t3

x=4 sin t

x=t2 1

4 x 1

ðèñ. 11

ðèñ. 12

ðèñ. 13

Пример 12.5. Найдите площадь фигуры, ограниченной кривой

( x

1 .

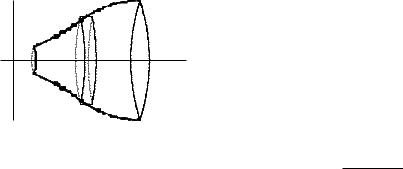
Решение . Заметим, что x > 1 и при замене t на t значения x не изменяются, а y меняет знак. Из этого следует, что фигура симметрична относительно оси OX и кривая имеет точку самопересечения, которая расположена на оси OX. Найдем эту точку. Имеем y = 0 при t = 0, t = 3. Точка самопересечения A(8; 0) (рис. 12). Найдем площадь части фигуры, расположенной в верхней полуплоскости и умножим ее на 2. Площадь вычислим по формуле (12.6).

S = 2	3	3	)2tdt = 4	3	2	4	t3	5	3	= 81 48; 6 = 32; 4.
S = 2	0	(9t t	)2tdt = 4	0	(9t	t )dt = 4	93	t5	0	= 81 48; 6 = 32; 4.
	R			R

Пример 12.6. Найдите площадь фигуры, ограниченной лемнискатой Бернулли

r2 = a2 cos 2'.

Решение . Òàê êàê r2 > 0 è a2 > 0, то cos 2' > 0. Тогда 2 + 2 n 66 2' 6 2 + 2 n. Следовательно 4 6 ' 6 4 è 34 6 ' 6 54 . Ôèãó-

ра симметрична относительно осей координат и начала координат (рис. 13), поэтому найдем площадь части фигуры, расположенной в 1-ой чет-

верти и умножим на 4. Площадь вычислим по формуле (12.7):

S =

sin 2' =4

cos 2'd' = 2a

= a

4 0 2a

Задания для самостоятельного

решения

Задание

12.1. Найдите

площадь

фигуры,

ограниченной

параболой

y = x2 2x 2 и прямой y = x + 2.

Задание

12.2. Найдите

площадь

фигуры,

ограниченной

параболой

y = x2 + 4x + 5 и прямой y = 1 x.

Задание

12.3. Найдите

площадь

фигуры,

ограниченной

параболой

y = x2 + 6x 3 и прямой y = 7 x.

Задание

12.4. Найдите

площадь

фигуры,

ограниченной

прямыми

y = x, y = 2x 1, y = 0; 5(x + 7).

Задание 12.5. Найдите площадь фигуры, ограниченной параболами y = x2 4x + 2 è y = x2 + 6x 6.

Задание 12.6. Найдите площадь фигуры, ограниченной параболами y = 2x2 + 4x 3 è y = x2 + 3x + 3.

Задание	12.7. Найдите	площадь	фигуры,	ограниченной	параболой
y = (x 3)2, прямой y = x + 3 и осью OX.
Задание	12.8. Найдите	площадь	фигуры,	ограниченной	параболой
y = (x + 1)2, прямой y = 10 0; 5x и осью OX.

Задание 12.9. Найдите площадь фигуры, ограниченной а) параболой y = x2 8x + 15 и осью OX; б) параболой y = x2 8x + 15 и осями

координат.

2 ,

Задание 12.10. Найдите площадь фигуры, ограниченной гиперболой y = x6 и прямой y = 7 x.

Задание 12.11. Найдите площадь фигуры, ограниченной гиперболой y = x8 и прямыми y = 2x, y = 0; 5x (x > 0).

Задание 12.12. Найдите площадь фигуры, ограниченной гиперболой

y =	12	x (x > 3).
	x и прямыми y = x + 1, y = 13

Задание 12.13.	Найдите площадь фигуры, ограниченной параболой
y = x3	y = 4x.
2 и прямой

Задание 12.14. Найдите площадь фигуры, ограниченной параболой p

y = 2x и прямыми y = x, y = 0; 5x.

Задание 12.15. Найдите площадь фигуры, ограниченной параболами y = y = x2, прямой y = 12 x и лежащей в первой четверти.

Задание 12.16. Найдите площадь фигуры, ограниченной прямыми y = x + 1, y = 3x 11 и y = 3 x.

Задание	12.17. Найдите площадь фигуры, ограниченной кривыми
y = x2	y =		1	.
		2	+ 1
2 è	x

Задание 12.18. Найдите площадь фигуры, ограниченной параболой y = x2 + 4x 5, касательной к ней в точке M0(2; 3) è îñüþ OY .

Задание 12.19. Найдите площадь фигуры, ограниченной параболой y = x2 6x + 11, касательной к ней в точке M0(4; 3) и осями координат.

Задание 12.20. Найдите площадь фигуры,	ограниченной	кривыми
y = e2x, y = e3 x и прямой y = 1.
Задание 12.21. Найдите площадь фигуры, ограниченной		а) петлей
кривой y2 = x2(4 x); б) петлей кривой y2 = 9x2 x4.
Задание 12.22. Найдите площадь фигуры,	ограниченной кривой
y = 3 cos2 t, x = 4 sin3 t è îñüþ OX (t 2 [0; ]).

i=0;:::;n 1

max


Задание		12.23. Найдите	площадь	фигуры,	ограниченной	кривой
y = t4	4t3 + 4t2 4t + 3, x = t2 + 3 è îñüþ OX (t 2 [1; 3]).
Задание		12.24. Найдите	площадь	фигуры,	ограниченной	кривой
y = t3	7t3 + 4t + 2, x = ln t + 3 è îñüþ OX (t 2 [1; 2]).
Задание		12.25. Найдите	площадь	фигуры,	ограниченной	кривой
y = t4	+ 2t3 t2 t + 5, x = ln t + 1 è îñüþ OX (t 2 [1; 3]).

Задание 12.26. Найдите площадь фигуры, ограниченной циклоидой y = 3(t + sin t), x = 3(1 + cos t).

Задание		12.27. Найдите				площадь	фигуры,	ограниченной	кривой
r = 3 + 2 cos '.
Задание		12.28. Найдите				площадь	фигуры,	ограниченной	кривой
r = 4(cos3 ' p					).
r = 4(cos3 ' p			sin 2'		).
Задание		12.29. Найдите				площадь	фигуры,	ограниченной	кривой
r = 2 tg ' и лучами ' = 0, ' =
						4 .
Задание		12.30. Найдите				площадь	фигуры,	ограниченной	кривой
r = 2p				и лучами ' = 0, ' = 3 .
r = 2p	1 + cos3'			и лучами ' = 0, ' = 3 .

Задание 12.31. Найдите площадь фигуры, ограниченной четырехлепестковой розой r = 16 cos 4'.

13. Применение определенного интеграла для вычисления длины дуги кривой.

Пусть дана кривая AB. Разделим ее на n частей точками A = A0; A1; : : : ; Ai; Ai+1; : : : ; An = B. Построим ломаную A0A1 : : : AiAi+1 : : : An. Обозна- чим через длину самого большого звена ломаной: = fjAiAi+1jg.

Конечный предел, к которому стремится длина ломаной при ! 0

называется длиной кривой AB. Если предел существует, то кривая называется спрямляемой.

Снова перейдем к параметрическому заданию кривой

Найдем длину звена AiAi+1. Если известны координаты точек, которые являются началом и концом звена Ai(xi; yi) è Ai+1(xi+1; yi+1), òî ïî

n 1

2.=

( xi)

+ ( yi)

2. Тогда длина ломаной

теореме

Пифагора

l = i=0 p

( xi) + ( yi)

x(t)

а) Кривая задана параметрически

( y

y(t) .

Если t 2 [ ; ], то пара (x(t); y(t)) задает все точки кривой. Пусть функ-

ции x(t) и y(t) дифференцируемы. Тогда						по теореме	Лагранжа
xi = x0( i) ti, yi = y0( i0) ti, ãäå i; i0 2 [ti; ti+1].
n 1
Длина ломаной ~l =			(x0( i))2		+ (y0( 0))2	ti. Ïðè		0 длина
ломаной приближается к		p
P					i		!
i=0					i		!
	длине кривой. Получаем формулу для вычис-
ления длины дуги кривой

l = Z
l = Z				(x0(t))2	+ (y0(t))2	dt:		(13:1)
		p

б) Кривая задана явно y = y(x), и x 2 [a; b].

Представим, что кривая задана параметрически, положив

Применив формулу (13.1), получим

l = 1 + (y0(x))2 dx

(

y = y(x) . x = x

(13:2)

в) Кривая задана в полярной системе координат r = r(') и ' 2 [ ; ].

(

y = r(') cos '

x = r(') sin ' . Найдем производные y0 = r0(') cos ' r(') sin ', x0 = r0(') sin ' +

r(') cos ' и подставим их в формулу (13.1). Применив основное тригонометрическое тождество, получим


l = Z
l = Z	((r('))2	+ (r0('))2	d':	(13:3)
	p

> x = x(t)

г) Пространственная кривая AB задана параметрически

y = y(t) ,

: z = z(t)

где t 2 [ ; ] и функции x(t), y(t), z(t) дифференцируемы. Проведя все рассуждения аналогично случаю а), получим


l = Z
l = Z	(x0	(t))2	+ (y0(t))2 + (z0(t))2	dt:		(13:4)
	p					4 sin3 t .
Пример 13.1. Вычислите длину дуги астроиды ( y					=	4 sin3 t .
				x	=	4 cos3 t

Решение . Кривая симметрична относительно осей координат и начала координат, поэтому найдем длину части кривой, расположенной в 1-ой четверти и умножим на 4. Параметр t это угол, образуемый радиус-вектором точки с положительным

направлением оси OX, следовательно, t 2 [0; =2]. Вычислим производные и найдем

подинтегральную функцию x0 = 12 cos2 t sin t, y0							= 12 sin2 t cos t.
p
	(x0)2 + (y0)2 = p144 cos4 t sin2 t + 144 sin4 t cos2 t = 12 sin t cos t psin2 t + cos2 t =
= 12 sin t cos t и вычислим длину дуги кривой, лежащей в 1-ой четверти
		=2		=2		=2
l1 =		0	12 sin t cos tdt =	0	12 sin td(sin t) = 6 sin2 t 0		= 6.
		R		R

Тогда длина всей кривой l = 4l1 = 24.

Пример 13.2. Вычислите длину дуги полукубической параболы

9y2 = x3 ïðè x 2 [0; 21].

Решение . Кривая симметрична относительно оси OX, поэтому найдем длину части

кривой, расположенной в 1-ой четверти и умножим на 2. В 1-ой четверти y =

Тогда y0

. Длина дуги

21 p

(4 + x)3

4 + x

l1 =

1 +

4 dx =

dx =

p 3

= 1253 8 = 39.

Длинаq

Rl = 2l1 = 78

всей кривой

Пример 13.3. Вычислите длину дуги кривой r = 3 cos

6 '

6 .

Решение . Чтобы найти при каких значениях аргумента получается один виток кривой r = 3 cos6 '6 , найдем при каких ' r = 0. Имеем cos '6 = 0, åñëè '6 = 2 + n. Таким образом, получаем ' 2 [ 3 ; 3 ]. Вычислим производную r0 = 3 cos5 '6 sin '6

и подинтегральную функцию pr2 + (r0)2 = q9 cos12 '6 + 9 cos10 '6 sin2 '6 = 3 cos5 '6 .

Задание 13.12.

Задание 13.11.

Длина дуги кривой

5 '

2 ' 2

5 '

l = 3

3 cos

3 (1 sin

d(sin

6 d' = 18

6 )

6 ) = 18

sin 6

3 sin

6 +

5 sin

3 =

= 18 1 3

+ 5 + 1

3 +

5 =

15.

Задания для самостоятельного решения

Задание

13.1. Вычислите длину

äóãè

кривой

4x,

åñëè

x 2 [0; 5; 2].

ln x

Задание

13.2. Вычислите длину дуги кривой

2 , åñëè

x 2 [1; 9].

Задание 13.3. Вычислите длину дуги кривой y2 = 4x3, åñëè x 2 [0; 11].

(x + 2)3

Задание 13.4. Вычислите длину дуги кривой y2

, åñëè

x 2 [0; 5; 2].

(8 3x)p

Задание 13.5. Вычислите длину дуги кривой y =

, åñëè

x 2 [2; 8].

Задание 13.6. Вычислите длину дуги кривой y = p

+ arcsin x.

1 x2

Задание 13.7. Вычислите длину дуги кривой

y =

x x

+ arcsin x

Задание

13.8. Вычислите

длину дуги кривой

t3 4t + 4,

+ 2

, åñëè

x = 4 3 t

t 2 [1; 3]

9; 6p

Задание

13.9. Вычислите длину дуги кривой

+ 0; 4,

y = t3 6t2 между точками пересечения с осью OX.

Задание

13.10. Вычислите

длину дуги кривой

(t 1)2et,

x = 2(t 1)et, åñëè t 2 [0; 1].

Вычислите длину дуги кривой y = t15, x = 1; 5t10 12 между точками пересечения с осями координат.

Вычислите длину дуги кривой y = (t2 2) sin t+2t cos t, x = (2 t2) cos t + 2t sin t, åñëè t 2 [0; ].

Задание 13.13. Вычислите длину дуги кривой y = 6 sin 2t + 2 cos 6t, x = 6 cos 2t 2 sin 6t, если t 2 [0; ].

Задание 13.14. Вычислите длину дуги кривой r = 5 cos4 '4 .

Задание 13.15. Вычислите длину дуги кривой r = 2(1 + sin ').

14. Применение определенного интеграла для вычисления объемов тел вращения.

Пусть на [a; b] задана неотрицательная функция y = f(x). Поставим задачу найти объем тела, полученного вращением вокруг оси OX криволинейной трапеции, ограниченной кривой y = f(x), и прямыми x = a, x = b. Для вычисления объема этого тела найдем объем тела, составлен-

ного из круговых цилиндров.

Разобьем отрезок [a; b] на n частей точками a = x0 < x1 < : : : < xi < xi+1 < : : : < xn = b. Для каждого i = 0; n 1 рассмотрим отрезок

[xi; xi+1]. Длины этих отрезков xi				= xi+1 xi. На каждом отрезке выбе-
рем точку i	2 [xi; xi+1], вычислим значения функции в этих точках f( i).
Найдем объемы цилиндров, радиусы оснований которых равен									f( i), à
Обозначим = max x1; x2; : : : ; xn						~	n 1	2
Обозначим = max x1; x2; : : : ; xn						, Тогда объем	P
высота xi. Тогда объем ступенчатого тела равен V =							f ( i) xi.
			f		g		i=0
							тела вращения

			n 1
равен V = lim			f2( i) xi. По определению определенного интеграла
	!	0	iP
		0	=0
			V = Za	b
			V = Za	f2(x) dx:					(14:1)

Пример 14.1. Вычислите объем тела, полученного вращением параболы y = x2 вокруг оси OX, если 0 6 x 6 2.

Решение . Согласно формуле (14.1) V =	2	2 2	2	4	dx =	x5	2	=	32
Решение . Согласно формуле (14.1) V =	0	(x ) dx =	0	x	dx =	5	0	=	5 .
	R		R

Пример 14.2. Вычислите объем тела, полученного вращением параболы y = x2 вокруг оси OY , если 0 6 x 6 2.

Решение . Так как вращение происходит вокруг оси OY , то y независимая переменная, а x = f(y). Имеем x = py и 0 6 y 6 4. Формула (14.1) примет вид

V = c	f (y) dy: Получаем	V =	0	(py) dy =	0	ydy =	2	4	= 2 = 8 .
								0
d	2		4	2	4		y2		16
R			R		R

Задания для самостоятельного решения

Задание 14.1. Найдите объем фигуры, образованной вращением вокруг оси OX и оси OY кривой а) y = 4 x2 ïðè x 2 [0; 2]; á) y = 2x x2

ïðè x 2 [0; 2].

15. Несобственные интегралы первого рода.

делена на конечном отрезке [aRa; b]. Если нарушается хотя бы одно из этих
В определенном интеграле	f(x) dx ограниченная функция f(x) опре-

условий, то интеграл не является определенным. Обобщим понятие определнного интеграла на случай, когда промежуток интегрирования бесконечен.

Пусть функция f(x) определена на промежутке [a; 1) и интегрируема на любом конечном промежутке [a; A], то есть для любого A > a

называется		A	A		от функции
называется		R	R		от функции
существует интеграл		f(x)dx. Если предел lim		f(x)dx конечен, то он
		a	A!1 a
	несобственным интегралом первого рода
f(x) на [a; 1) и обозначается
		+1	A
		Za	= A!1 Za		(15:1)
		f(x) dx	lim f(x) dx:		(15:1)

Если конечный предел определенного интеграла существует, то говорят, что несобственный интеграл (15.1) сходится, а если предел не существует, то говорят, что интеграл (15.1) расходится.

Аналогично определяем несобственные интегралы по промежуткам ( 1; b] и ( 1; 1) соответственно

	b				b
	Z	f(x) dx	= B! 1 Z			(15:2)
		f(x) dx		lim	f(x) dx:	(15:2)
1					B
	+1				A
	Z	f(x) dx =		B!!11 Z		(15:3)
		f(x) dx =		lim	f(x) dx:	(15:3)
				A
	1				B
	, если существует				+1
	, если существует				R
Говорят, что несобственный интеграл					f(x) dx сходится в смысле
					1
главного значения					предел
	+1				A
	Z	f(x) dx =		A!+1 Z		(15:4)
		f(x) dx =		lim	f(x) dx:	(15:4)
1					A

Существуют примеры, когда интеграл сходится в смысле главного зна-
чения и расходится в обычном смысле.
					+1
Несобственный интеграл Ra f(+ )							dx называется сходящимся абсо-
						x	dx называется сходящимся абсо-
						1
лютно, если сходится интеграл						Ra	jf(x)j dx.
+1		15.1.	Если интеграл			+1
+1		15.1.	Если интеграл			Ra	jf(x)j dx
Теорема								сходится, то интеграл
Ra	f(x) dx также сходится.						+1
Заметим, что			+				Ra
			из сходимости интеграла					f(x) dx не следует сходи-
				1
мость интеграла			Ra		jf(x)j dx.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.09.2019415.81 Кб1ОМПТ.docx
#
11.05.2015235.22 Кб23ОМПТ.pdf
#
11.05.201528.16 Кб239ООО.doc
#
11.05.20155.98 Mб74ОПЕС. Практикум. УКО.pdf
#
11.05.20153.65 Mб177ОПЕС. Учебник.pdf
#
11.05.2015636.3 Кб4опред-интеграл-stud.pdf
#
01.08.20194.07 Mб4ОПТ ЛР 2.docx
#
21.11.2019131.58 Кб1Оптимизация учета Постановка документооборота.doc
#
21.04.20191.44 Mб7Организация и управление.doc
#
20.12.2018105.93 Кб4организация производства моя.docx
#
11.05.20154.55 Mб818орлик Основы программной инженерии.pdf