
Краткий курс математического анализа. Том 2
.pdf
130 Гл. 5. Интегральное исчисление функций многих переменных
Из неравенств (42.55) и (42.63) вытекает равенство (42.57), т. е. свойство 4.
Отметим, что как нижняя, так и верхняя меры множества не обладают свойствами аддитивности. Это видно уже в одномерном случае. Например, если X1 — множество рациональных, а X2 — иррациональных точек отрезка [0, 1], то
μ X1 = μ X2 = 0, μ (X1 X2) = μ [0, 1] = 1 = 0 = μ X1 + μ X2, μ X1 = μ X2 = 1, μ (X1 X2) = μ [0, 1] = 1 = 2 = μ X1 + μ X2.
З а м е ч а н и е 11. Добавление к измеримому множеству множества меры нуль или вычитание его из измеримого множества не нарушает измеримости исходного множества (это следует из свойства 3 меры, поскольку множества меры нуль измеримы) и не меняет его меры (а это следует непосредственно из свойства 4 меры). В частности, если X — измеримое множество, то измеримы его замыкание X и множество Xint его внутренних точек, причем
|
|
|
|
|
|
|
|
|
(42.64) |
|
|
μXint = μX = μX |
. |
||||||
Действительно, |
|
|
|
|
|
||||
X = Xint (X \ Xint), |
X \ Xint ∂X, |
|
|||||||
|
|
= X ( |
|
\ X), |
|
|
|
||
X |
X |
X \ X ∂X. |
|
||||||
По теореме 1 имеем μ∂X = 0, поэтому
μ(X \ Xint) = μ(X \ X) = 0,
и, следовательно, имеет место равенство (42.64). В частности, если μX = 0, то μX = 0.
З а м е ч а н и е 12. Замыкание измеримого множества, как и замыкание всякого ограниченного множества, является компактом. Таким образом, замыкание измеримого множества есть измеримый компакт.
С в о й с т в о 5. Мера множества не меняется при параллельном переносе.
Прежде чем доказывать это утверждение, докажем еще одну лемму.
Л е м м а 5. Если
Xk X Yk,
Xk, Yk — измеримые множества, k = 1, 2, ..., и
lim μ(Yk \ Xk) = 0,
k→∞
то множество X также измеримо и
μX = lim μXk = lim μYk.
k→∞ k→∞

|
|
|
§ 42. Кратные интегралы |
|
|
|
|
|
|
|
|
|
131 |
|||||
Действительно, если положить |
X |
= (X |
) |
|
|
|
, Y = |
|
|
, |
то будем |
|||||||
int |
Y |
|
||||||||||||||||
|
k |
k |
|
k |
k |
|
||||||||||||
иметь |
μXk |
= μ(Xk)int = μXk, |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
μYk = μY |
k = μYk, |
|
|
|
|
|||||||||||
а поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
μ(Y |
X ) = |
lim μY |
lim μX |
= lim μY |
lim μX |
|
= |
||||||||||
k→∞ |
k \ |
k |
k→∞ |
k |
− k→∞ |
|
k |
k→∞ |
|
|
|
k − k→∞ |
|
|
k |
|
||
= lim μ(Yk \ Xk) = 0.
k→∞
Из включений X X Yk , Xk Xint имеем ∂X = X \ XintYk \ Xk. Поэтому имеет место неравенство μ ∂X μ(Yk \ Xk),
откуда при k → ∞ получаем μ ∂X = 0, а значит, и μ∂X = 0. Это согласно теореме 1 означает измеримость множества X. (Ограниченность множества X, которая требуется в условиях теоремы 1, следует из включения X Yk и ограниченности множества Yk, как всякого измеримого множества.)
Далее, X \ Xk Yk \ Xk, Yk \ X Yk \ Xk, поэтому
μ(X \ Xk) μ(Yk \ Xk), μ(Yk \ X) μ(Yk \ Xk),
где klim μ(Yk \ Xk) = 0, а следовательно, в силу аддитивности меры |
|
→∞ |
|
klim (μX − μXk) = klim (μYk − μX) = 0. |
|
→∞ |
→∞ |
Докажем теперь свойство 5 меры. |
|
Пусть X — измеримое |
множество, X Rn, a = (a1, a2, ..., an), |
X + a = {x + a : x X}. Если Q — n-мерный куб с ребрами длины h и параллельными осям координат, то множество Q + a также является кубом того же вида и, следовательно, измеримым множеством, причем (см. замечание 4)
μ(Q + a) = μQ = hn.
Для каждого натурального k множества Xk = sk(X) + a, Yk = = Sk(X) + a измеримы, так как являются объединением конечного числа измеримых множеств вида Q + a, где Q — куб ранга k, и
μXk = μsk(X), μYk = μSk(X),
ибо меры множеств Xk и Yk равна сумме мер (как в формуле (42.6)), составляющих их кубов.
Поскольку
Xk X + a Yk
и
klim μ(Yk \ Xk) = klim (μYk − μXk) = klim (μSk(X) − μsk(X)) = 0, |
||
→∞ |
→∞ |
→∞ |
5*

132 Гл. 5. Интегральное исчисление функций многих переменных
то согласно лемме 5 множество X + a измеримо и
μ(X + a) = lim μXk = lim μsk(X) = μX.
k→∞ k→∞
З а м е ч а н и е 13. Рассмотрим (n + 1)-мерное пространство Rn+1 как произведение n-мерного Rn и числовой оси R:
Rn+1 = Rn ×R.
Если X Rn, [a, b] R, то множество X × [a, b] точек (x1, ..., xn, y),
(x1, ..., xn) X, y [a, b], называется цилиндром с основанием X
(см. п. 40.2) и образующей [a, b].
Можно доказать, что если X — измеримое в смысле n-мерной меры множество, то цилиндр X × [a, b] измерим в смысле (n + 1)-мерной
меры и |
|
μn+1(X × [a, b]) = (b − a)μnX. |
(42.65) |
У п р а ж н е н и е 2. Доказать утверждения замечания 13.
42.2. Множества меры нуль. Укажем два типа множеств, мера Жордана которых всегда равна нулю (на подобные множества нередко удается разбить границу рассматриваемых множеств и тем самым доказать их измеримость).
Т е о р е м а 2. График всякой непрерывной на компакте функции имеет меру Жордана, равную нулю.
Пусть X Rn, X — компакт, y = f (x) — непрерывная на X функция, x X, y R и
Y= {(x, y) : x = (x1, ..., xn) X, y = f (x)} Rn+1
—график функции f. Покажем, что (n + 1)-мерная мера множества Y равна нулю.
Из компактности множества X следует его ограниченность. Поэтому существует n-мерный куб Qn(m) вида
Qn(m) = {x : |xi| m, i = 1, 2, ..., n}, |
(42.66) |
содержащий множество X:
X Qn(m).
Обозначим через Qn(m + 1) куб, определяемый аналогично (42.66) с заменой m на m + 1. Тогда ясно, что
X Sk(X) Qn(m + 1), k = 1, 2, ... |
(42.67) |
||
Множество Sk(X) состоит из некоторого конечного числа |
ik n-мер- |
||
ных кубов ранга k; занумеруем их индексами i и обозначим Qn |
, |
||
i = 1, 2, ..., ik: |
|
k,i |
|
|
|
|
|
i |
|
|
|
ik |
|
|
|
Sk(X) = Qn |
. |
(42.68) |
|
k,i |
|
|
|
=1 |
|
|
|

§ 42. Кратные интегралы |
133 |
Для каждого куба Qn |
обозначим через P n+1 |
объединение («стол- |
||
|
k,i |
|
k,i |
|
бик») всех (n + 1)-мерных кубов ранга k, |
содержащихся в Sk(Y ) |
|||
и проецирующихся в указанный n-мер- |
|
|
||
ный куб Qn |
(рис. 23). Тогда |
|
|
|
k,i |
i |
|
|
|
|
|
|
|
|
|
ik |
|
|
|
Sk(Y ) = Pkn,+i 1, |
(42.69) |
|
|
|
|
=1 |
|
|
|
т. е. Sk(Y ) можно представить в виде объединения столбиков Pkn,+i 1.
Обозначим через h(kn,i) высоту столбика Pkn,+i 1, тогда
(kn,i)μnQnk,i, i = 1, 2, ..., ik.
(42.70)
Пусть ωk,i(f ) — колебание функции f на пересечении X ∩ Qnk,i компакта X с кубом Qnk,i, т. е. верхняя грань разностей f (x ) − f (x), когда x, x X ∩ Qnk,i (см. (35.2)). Тогда (см. рис. 23, n = 1, X = [a, b])
hk(n,i) ωk,i(f ) + |
2k , i = 1, 2, ..., ik. |
(42.71) |
|
10 |
|
Зададим теперь произвольно ε > 0. Поскольку функция f непрерывна на компакте X, то она и равномерно непрерывна на нем (теорема 2 из п. 35.1). Следовательно, существует такое δ > 0, что для любого множества E X, diam E < δ, колебание ω(f ; E) функции f на множестве E удовлетворяет неравенству ω(f ; E) < ε. Поэтому, если ранг k таков, что диаметр 10−k√n куба ранга k меньше δ, то колебание ωk,i(f ) функции f на пересечении X ∩ Qnk,i меньше ε,
так как
diam X ∩ Qnk,i diam Qnk,i < δ.
Второе слагаемое в правой части неравенства (42.71) стремится
к нулю при k |
→ ∞ |
, |
поэтому |
существует такой ранг k , что при k > k |
|||||||
|
|
|
|
|
2 |
|
0 |
0 |
|||
выполняется неравенство ωk,i(f ) + |
10k < ε, а следовательно, в силу |
||||||||||
(42.71) и неравенство |
|
h(n) |
|
|
|
|
(42.72) |
||||
|
|
|
|
|
|
< ε. |
|
|
|||
|
|
|
|
|
|
k,i |
|
|
|
|
|
В результате при k > k0 имеем |
|
|
|
|
|
||||||
|
|
ik |
|
|
|
|
|
ik |
|
|
|
|
|
|
μn+1P n+1 |
|
i |
|
|
|
|||
μn+1Sk(Y ) = |
|
|
= |
|
h(n)μnQn |
< |
|
||||
(42.69) |
i=1 |
k,i |
|
(42.70) |
|
k,i |
k,i |
(42.72) |
|
||
|
|
|
|
|
|
=1 |
|
|
|
||
|
|
|
|
ik |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
= εμnSk(X) εμnQ(m + 1). |
|||
|
|
|
|
< ε μnQkn,i |
|
||||||
|
|
(42.72) |
|
|
|
(42.68) |
|
(42.67) |
|
||
|
|
|
|
=1 |
|
|
|
|
|
|
|
134 Гл. 5. Интегральное исчисление функций многих переменных
Поскольку ε > 0 было выбрано произвольно, а μnQ(m + 1) — фиксированное число, то
lim μn+1Sk(Y ) = 0.
k→∞
Это и означает, что μn+1Y = 0.
Из теоремы 2 следует, что если граница подмножества n-мерного пространства представима как объединение конечного числа графиков непрерывных на некоторых компактах функций n − 1 переменных, то это подмножество измеримо по Жордану, так как его граница имеет n-мерную меру Жордана, равную нулю.
Простейшими примерами таких множеств являются n-мерные параллелепипеды и шары. Отметим, что при n = 2 к множествам этого типа относятся и криволинейные трапеции (см. п. 28.1), а при n = 3 тела вращения, рассмотренные в п. 28.5. Этим и объясняется то, что при определении площадей и, соответственно, объемов этих множеств мы обошлись лишь понятием внутренней меры μ (см. п. 27.1 и п. 27.2).
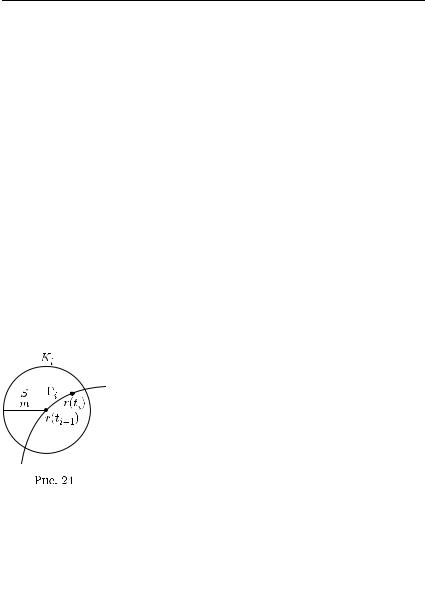
Те о р е м а 3. Всякая плоская спрямляемая кривая имеет двумерную меру (площадь), равную нулю.
Пусть Γ = {r = r(t), a t b} — плоская спрямляемая кривая (r(t) — точка плоскости R2) и S — ее длина. Разобьем кривую Γ
точками r(ti), a = t0 < t1 < ... < ti < ... < tm = b,
на m равных по длине дуг Γi = {r = r(t), ti−1t ti}, i = 1, 2, ..., m: длина Γi равна
|
|
|
|
|
|
|
|
|
|
|
S |
. |
|
|
|
(42.73) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
Пусть Ki — замкнутый круг с центром в точке |
|||||||||||
|
|
|
|
|
r(ti−1) и радиуса S/m; тогда (см. рис. 24) |
|||||||||||
|
|
|
|
|
i |
|
|
Γi(42.73)Ki, i = 1, 2, ..., m, |
|
|||||||
|
|
|
|
|
m |
|
m |
m |
|
|
|
|||||
|
|
|
|
|
m |
|
m |
|
|
|
|
|
|
|
||
и, следовательно, Γ = =1 |
Γi |
i=1 Ki. Поэтому |
|
|
|
|
||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
2 |
|
|||
μ Γ (42.25) |
μ |
i=1 Ki |
(42.53) i=1 μ Ki = i=1 μKi = i=1 π |
S |
|
= |
||||||||||
m |
||||||||||||||||
|
|
|
|
|
|
|
2 |
m |
|
2 |
|
|
|
|
|
|
|
|
|
|
= π |
S |
|
|
1 = |
πSm → 0 |
при m → ∞. (42.74) |
||||||
|
|
|
|
m |
i=1 |
|||||||||||
Мы воспользовались здесь равенством μ Ki = μKi. Справедливость его вытекает из того, что круг — измеримое множество, так как его границу можно представить в виде объединения двух полуокружностей, каждая из которых является непрерывной на отрезке функцией
§ 42. Кратные интегралы |
135 |
и, следовательно, по теореме 2 имеет меру нуль. Поэтому круг, согласно теореме 1, — измеримое множество.
Из (42.74) имеем μ Γ = 0. Это и означает (см. замечание 1 в п. 42.1), что μΓ = 0.
Кривая называется кусочно-гладкой, если ее можно представить в виде конечного объединения гладких кривых (п. 17.2).
Как известно (п. 17.3), всякая гладкая кривая спрямляема, поэтому спрямляемы и кусочно-гладкие кривые. Отсюда, согласно теореме 3, следует, что всякое ограниченное множество на плоскости, граница которого состоит из конечного числа кусочно-гладких кривых, является квадрируемым.
З а м е ч а н и е 1. Аналогично теореме 3 доказывается, что n-мер- ная мера спрямляемой кривой, лежащей в n-мерном пространстве, равна нулю. Для этого в доказательстве теоремы 3 достаточно круги, которыми покрывается рассматриваемая кривая, заменить соответствующими шарами.
З а м е ч а н и е |
2. Если множество X имеет n-мерную меру нуль, |
то цилиндр X × |
[a, b] имеет (n + 1)-мерную меру нуль. Это сразу |
следует из формулы (42.65).
42.3. Разбиение измеримых множеств. Пусть X — измеримое по Жордану множество, лежащее в пространстве Rn. Конечная
система τ = {Xj }jj==1jτ |
измеримых множеств Xj , j = 1, 2, ..., jτ , назы- |
|||
вается разбиением множества X, если: |
|
|||
|
|
|
jτ |
|
1) μ(Xj ∩ Xi) = 0 |
при j = i; 2) |
=1 Xj = X. |
||
Число |
def |
max |
j |
, |
|
|
diam Xj |
||
|
|τ | = j=1,2,...,jτ |
|
||
где diam Xj — диаметр множества Xj , называется мелкостью разбиения τ .
Если τ = {Xj }jj==j1τ и τ = {Xi }ii==i1τ — два разбиения множества X и для каждого Xi τ существует такое Xj τ , что Xi Xj , то го-
ворят, что разбиение τ вписано в разбиение τ (или, что разбиение τ
следует за разбиением τ ), и пишут τ τ или, что то же самое, τ τ .
С в о й с т в а р а з б и е н и й.
1◦ (т р а н з и т и в н о с т ь). Если τ τ и τ τ , то τ τ . Это непосредственно вытекает из определения следования одного
разбиения за другим (ср. с соответствующим свойством разбиения
отрезка на отрезки в п. 23.1).
2◦ (ф и н а л ь н о с т ь). Для любых двух разбиений τ и τ множества X существует его разбиение τ , следующее и за τ , и за τ :
τ τ , τ τ .

136 Гл. 5. Интегральное исчисление функций многих переменных
За элементы разбиения τ можно взять всевозможные пересечения элементов разбиений τ и τ .
Л е м м а 6. Если τ = {Xj }jj==j1τ — разбиение множества X, то
jτ
μX = μXj .
j=1
Пусть X — объединение всевозможных попарных пересечений различных множеств Xj τ (эти пересечения по определению разбиения имеют меру нуль), т. е.
X = Xi ∩ Xj .
i=j
Сумма конечного множества множеств меры нуль также имеют меру нуль:
μX = 0. |
(42.75) |
Обозначим через Xj множество, получающееся из множества Xj удалением из него точек множества X :
Xj = Xj \ X .
Если из множества вычесть множество меры нуль, то его мера не изменится. Поэтому
μX = μX |
, |
j = 1, 2, |
... |
, j . |
(42.76) |
|
j |
j |
|
|
τ |
|
|
Множества Xj попарно и с множеством X не пересекаются. Очевидно, имеет место равенство
|
j |
|
X = |
jτ |
(42.77) |
=1 Xj X , |
причем слагаемые его правой части не пересекаются. Поэтому, используя аддитивность меры, получим
jτ |
|
jτ |
|
|
jτ |
|
|
|
μX + μX |
j |
μX |
= |
|
|
|
μX = |
= |
μX |
. |
||||
(42.77) |
j |
(42.75) |
j |
(42.76) |
j |
|
|
j=1 |
|
=1 |
|
|
j=1 |
|
|
Л е м м а 7. У всякого измеримого множества существуют разбиения сколь угодно малой мелкости.
Пусть X — измеримое множество, X Rn. Обозначим через Xk,j , j = 1, 2, ..., jk, всевозможные непустые пересечения кубов ранга k
с множеством X. Таким образом, для каждого |
j = 1, 2, ..., jk суще- |
ствует такой куб ранга k, обозначим его Qk,j , что |
|
Xk,j = X ∩ Qk,j = . |
(42.78) |

§ 42. Кратные интегралы |
137 |
Система множеств
τk = {Xk,j}jj==j1k
образует разбиение множества X. Действительно, множества Xk,j измеримы как пересечение двух измеримых множеств X и Qk,j , их объединение составляет множество:
jk
X = Xk,j.
j=1
Пересечения множеств Xk,j имеют меру нуль. В самом деле, при i = j имеем
Xk,i ∩ Xk,j Qk,i ∩ Qk,j ∂Qk,i ∩ ∂Qk,j ,
(42.78)
и так как для любого куба мера его границы равна нулю, то
μ(Xk,i ∩ Xk,j ) μ(∂Qk,i ∩ ∂Qk,j ) μ∂Qk,i = 0, i = j.
Мелкость разбиения τk стремится к нулю при k → ∞:
lim |τk| = 0.
k→∞
Это следует из того, что диаметр n-мерного куба ранга k равен и потому
√
10nk ,
|
|
√ |
|
|
|
|
|
|τk| = j=1,2,...,jk |
diam Xk,j diam Qk,j = |
n |
→ |
|
при k → ∞. |
||
10k |
|
||||||
max |
|
|
|
|
|
0 |
|
42.4. Интегральные суммы. Определение кратного интеграла. Пусть на измеримом множестве X Rn определена функция f , τ = {Xj }jj==j1τ — разбиение множества X, ξ(j) Xj , j = 1, 2, ...
|
|
jτ |
..., jτ , |
def |
f (ξ(j))μXj . Всякая сум- |
и στ ≡ στ (f ) ≡ στ (f ; ξ(1), ..., ξ(jτ )) = |
j=1
ма этого вида называется интегральной суммой Римана функции f , соответствующей разбиению τ .
О п р е д е л е н и е 2. Функция f называется интегрируемой по Риману на множестве X, если один и тот же конечный предел имеет
любая последовательность интегральных сумм
|
|
jm |
|
|
|
j |
(m), |
στ |
= |
f (ξ(j,m))μX |
|
|
m |
|
j |
|
|
=1 |
|
соответствующих разбиениям τm = {Xj(m)}jj==j1m множества X, у которых их мелкость |τm| стремится к нулю при m → ∞, т. е.
lim |τm| = 0,
m→∞

138 Гл. 5. Интегральное исчисление функций многих переменных
а точки ξ(j,m) выбраны произвольным образом в множествах Xj(m):
ξ(j,m) Xj(m), j = 1, 2, ..., jm, m = 1, 2, ...
Этот предел, если он существует, называется интегралом Римана от функции f по множеству X и обозначается
f (x) dx.
X
Таким образом,
def |
(f ; ξ(1,m), ..., ξ(jm,m)). |
(42.79) |
f (x) dx = lim στm |
||
m→∞ |
|
|
X
Условие (42.79) равносильно тому, что существует число, обозначаемое f (x) dx, которое удовлетворяет следующему условию:
X |
|
|
каково бы ни было ε > 0, найдется такое δ > 0, что для любого |
||
разбиения τ = {Xj }jj==1jτ |
множества X мелкости |τ | < δ и при любом |
|
выборе точек ξ(j) Xj , |
j = 1, 2, ..., jτ , имеет место неравенство |
|
X f (x) dx − στ (f ; ξ(1), ..., ξ(jτ )) < ε. |
(42.80) |
|
|
|
|
|
|
|
Доказательство эквивалентности условий (42.79) и (42.80) проводится аналогично доказательству эквивалентности определения предела функции в терминах последовательности и в терминах окрестностей (см. п. 6.4).
У п р а ж н е н и е 3. Доказать эквивалентность условий (42.79) и (42.80).
Выполнение условия (42.79), или, что равносильно, условия
(42.80), коротко записывают равенством |
|
lim στ = f (x) dx |
(42.81) |
|τ|→0 |
|
X
и говорят, что интеграл f (x) dx является пределом интегральных
X
сумм στ при |τ | → 0.
Множество X, по которому производится интегрирование, часто называют областью интегрирования.
Вместо «функция, интегрируемая по Риману», и «интеграл Римана» будем для краткости говорить просто «интегрируемая функция»
§ 42. Кратные интегралы |
139 |
и «интеграл». Если n > 1, то интеграл f (x) dx называется кратным
интегралом. Его обозначают также |
X |
|
... f (x1, ..., xn) dx1... dxn.
X
В случае n = 2 он называется двойным, в случае n = 3 — тройным интегралом, а в случае произвольного n N — n-кратным.
З а м е ч а н и е 1. Интегральные суммы являются функциями, аргументами которых являются разбиения τ и точки ξ(j), j = 1, 2, ..., jτ , лежащие в элементах этих разбиений. Однако предел интегральных сумм это не предел функции, а принципиально новое понятие. При переходе к пределу интегральных сумм их аргументы τ и ξ(j), j = 1, 2, ..., jτ , изменяются, но ни к чему не стремятся, и здесь нельзя, как в случае предела функции, указать «точку» (τ , ξ(1), ..., ξ(jτ )),
вкоторой берется предел интегральных сумм.
За м е ч а н и е 2. Можно показать, что в случае n = 1 и X = [a, b] (т. е. когда X — отрезок) определения интеграла по отрезку в смысле ранее данного определения в п. 32.1 (т. е. когда рассматривались интегральные суммы, соответствующие только разбиению отрезка на отрезки) и в смысле определения этого пункта (т. е. когда рассматриваются интегральные суммы, соответствующие разбиению отрезка на произвольные измеримые множества) равносильны, т. е. приводят к одному и тому же понятию интеграла.
З а м е ч а н и е 3. В дальнейшем нам не раз придется встречаться с пределами типа (42.81) в несколько более простой ситуации, а именно, когда задана некоторая функция F (τ ), определенная на множестве всех разбиений τ некоторого измеримого множества X (таким образом, здесь F (τ ) зависит только от τ , в отличие от интегральных
сумм, которые зависят еще от точек ξ(j), j = 1, 2, ..., jτ ).
Будем говорить, что число a является пределом функции F (τ ) при
|τ | → 0, и писать |
lim F (τ ) = a, |
(42.82) |
|
|τ|→0 |
|
если для любого ε > 0 существует такое δ > 0, что для всех разбиений τ мелкости |τ | < δ имеет место
|F (τ ) − a| < ε.
У п р а ж н е н и е 4. Сформулировать в предположениях замечания 3 определение предела функции F (τ ) при |τ | → 0 в терминах пределов последовательностей так, чтобы оно было равносильно определению (42.82).
42.5. Неполные интегральные суммы. Введем еще обозначения, которые мы будем неоднократно использовать.
