Эллиптический цилиндр

Определение 47.8 Эллиптическим цилиндром называется поверхность, координаты всех точек которой в некоторой системе удовлетворяют уравнению

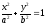
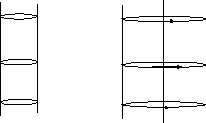
Рис.47.15 Рис.47.16

В сечении эллиптического цилиндра плоскостями могут получиться:

-эллипс (если плоскость не параллельна образующей цилиндра или не проходит через неё; читателю предлагается самостоятельно показать, что в сечении эллиптического цилиндра такой плоскостью должна получиться некоторая ограниченная кривая второго порядка, т.е. эллипс);

-две прямые параллельные линии (когда плоскость параллельна образующей цилиндра или проходит через неё, а также пересекает, но не касается эллиптического цилиндра)

-одна прямая линия (для плоскости, касающейся эллиптического цилиндра);

-пустое множество (в случае, когда плоскость не пересекает эллиптический цилиндр).

II. Гиперболический цилиндр

Определение 47.9 Гиперболическим цилиндром называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению:

(34.1)

Общий вид гиперболического цилиндра изображён на рис.47.17

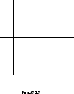
В сечении гиперболического цилиндра плоскостями могут получиться:

-гипербола (когда секущая плоскость не параллельна образующей гиперболического цилиндра или не пересекает её; читателю предлагаем самостоятельно доказать, что в этом случае в секущей плоскости должна получиться некоторая разрывная кривая второго порядка, т.е. гипербола);

- две прямые параллельные линии (в случае, если плоскость параллельна образующей гиперболического цилиндра (оси аппликат OZ) или проходит через неё, а также пересекает поверхность, но не касается её);

-одна прямая линия (для плоскости, касающейся цилиндрической поверхности);

-пустое множество (в случае, когда плоскость не пересекает гиперболический цилиндр).

III. Параболический цилиндр

Определение 47.10. Параболическим цилиндром называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению:

(34.3)

Общий вид параболического цилиндра изображён на рис. 47.18.

В сечении параболического цилиндра плоскостями могут получаться:

-парабола (когда секущая плоскость не параллельна образующей параболического цилиндра или не пересекает её; читателю предлагаем самостоятельно доказать, что в этом случае в секущей плоскости должна получиться некоторая неограниченная непрерывная кривая второго порядка, т.е. парабола)

- две прямые параллельные линии (если секущая плоскость параллельна образующей параболического цилиндра (оси аппликат OZ) или проходит через неё, а также пересекает поверхность, но не касается её); или параллельна плоскости

-одна прямая линия (в случае, когда плоскость касается цилиндрической поверхности);

-пустое множество (для плоскости, не пересекающей параболический цилиндр).

Остальные цилиндрические поверхности являются распадающимися или вырожденными (согласно, например, параграфу 35) и будут рассмотрены в п. 47.7.

Ж) Конус второго порядка

Конусом второго порядка называется поверхность, координаты всех точек которой в некоторой системе координат удовлетворяют уравнению

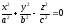(47.8)

Отметим, что если координаты точки 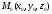удовлетворяют уравнению (47.8), то и для любого действительногоt координаты точки также удовлетворяют этому уравнению.

Поэтому, если точка 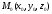лежит на конусе (47.8), то и вся прямая