
Яхъяев - Техническое черчение
.pdf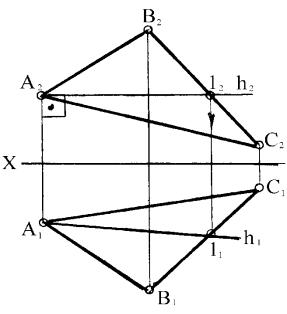
Горизонталь плоскости – это линия плоскости, параллельная горизонтальной плоскости проекций(рисунок 45). Построение горизонтали всегда начинают с ее фронтальной проекции. Так как
горизонталь плоскости есть прямая параллельная плоскости 1, то фронтальная проекция этой прямой
h А2А1. Для построения горизонтальной проекции горизонтали строим
точку 11 и проводим прямую h1 через точки А1 и 11. Алгоритм решения:
h (А,1) (АВС); h2 А2; h2 А2А1; h2 В2С2 = 12;
1211,1211 А2А1; 1211 В1С1 = 11; А1 11 = h1.
Рисунок45 В плоскости, заданной следами (рисунок 46), горизонталь плоскости задается принципиально таким же образом.
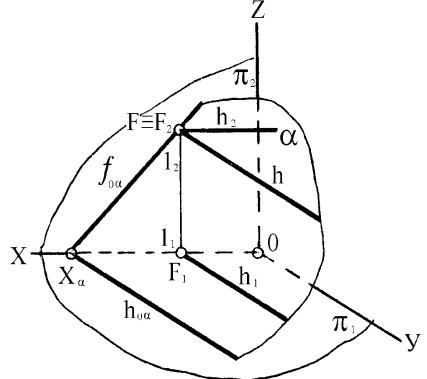
Рисунок 46 |
|
Чтобы построить произвольную горизонталь плоскости |
, |
заданной на эпюре следами (рисунок 47), достаточно:
а) провести в произвольном месте чертежа (рисунок 47) прямую линию
h2 Х (фронтальная проекция горизонтали параллельна оси Х), найти фронтальный след горизонтали 1(12; 11) и через точку 11 провести
h1 h (горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости);
б) провести в произвольном месте чертежа (рисунок 47) прямую
h1 h , найти фронтальный след горизонтали 1(11;12) и через точку 12 провести прямую h2 Х.
Фронталь плоскости – это линия плоскости, параллельная фронтальной плоскости проекций (рисунок 48). Построение начинают с горизонтальной плоскости.
Алгоритм решения:
f (F,1) (DEF); f1F1; f1 F1F2; f1 D1E1 11; 1112 F1F2; 1112 D2E2 12; F2 12 f2.
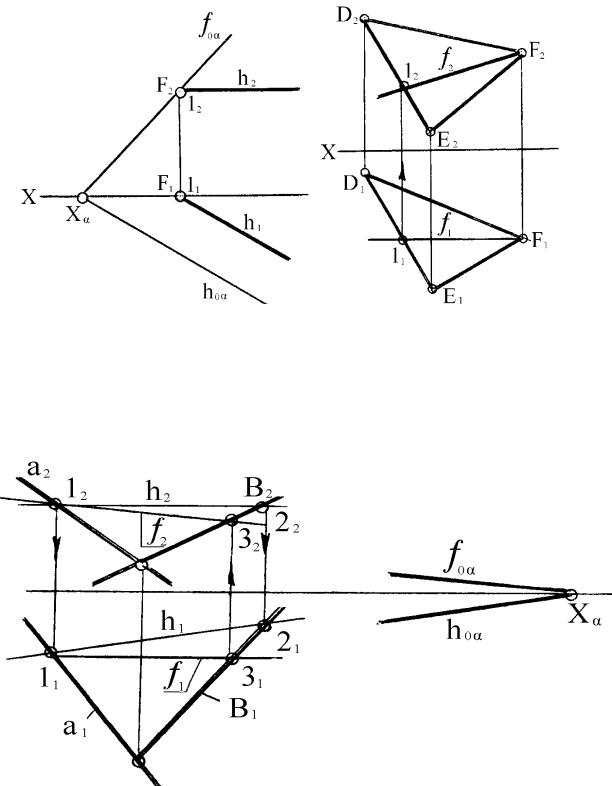
Рисунок 47 |
Рисунок 48 |
Используя горизонталь и фронталь плоскости, можно построить следы плоскости. Проведем в плоскости (a b) горизонталь h и фронтальf(рисунок 49).Найдяфронтальную проекцию фронтального следа горизонтали – точку 32 , проведем через нее f f2. Отметим точку Х пересечения прямой f с осью Х, проведем через нее h h1.
Рисунок 49
У плоскостей, заданных следами, горизонтальная проекция фронтали параллельна оси Х (f1 Х), горизонтальный след фронтали принадлежит горизонтальному следу плоскости (h hо ), и фронтальная проекция фронтали параллельна фронтальному следу
плоскости f f (рисунок 50). f,
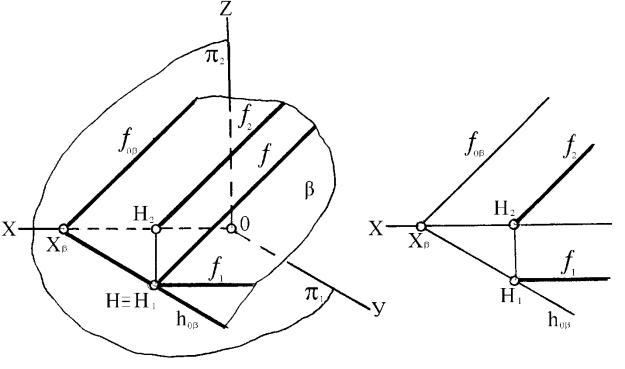
(hо , f ), f 2.
Рисунок 50
Линиями наклона плоскости называют прямые плоскости, перпендикулярные к линиям уровня. Название их связано с тем, что эти линии образуют с соответствующими плоскостями проекций углы, по величине равные углам наклона плоскости к плоскостям проекций.
Из трех линий наибольшего наклона к плоскостям проекций отметим
линию наибольшего наклона к плоскости 1. Эту линию называют
линией ската. Линия ската – прямая лежащая в плоскости и перпендикулярная ее горизонталям. Для проведения линии ската в
плоскости (a b) предварительно должна быть определена горизонталь плоскости h (рисунок 51) . После этого горизонтальная проекция линии ската проводится перпендикулярно к горизонтальной проекции горизонтали (4131 h1), а фронтальная проекция определяется точками 32 и 42 пересечения ее с данными линиями плоскости.
На рисунке 52 через точку В проведена линия l наклона плоскости (АВС) к фронтальной плоскости проекций. Ее фронтальная проекция (В212) перпендикулярна к фронтальной проекции А2С2 прямой АС, являющейся фронталью, а горизонтальная проекция определена точкой 11 пересечения с прямой АС.
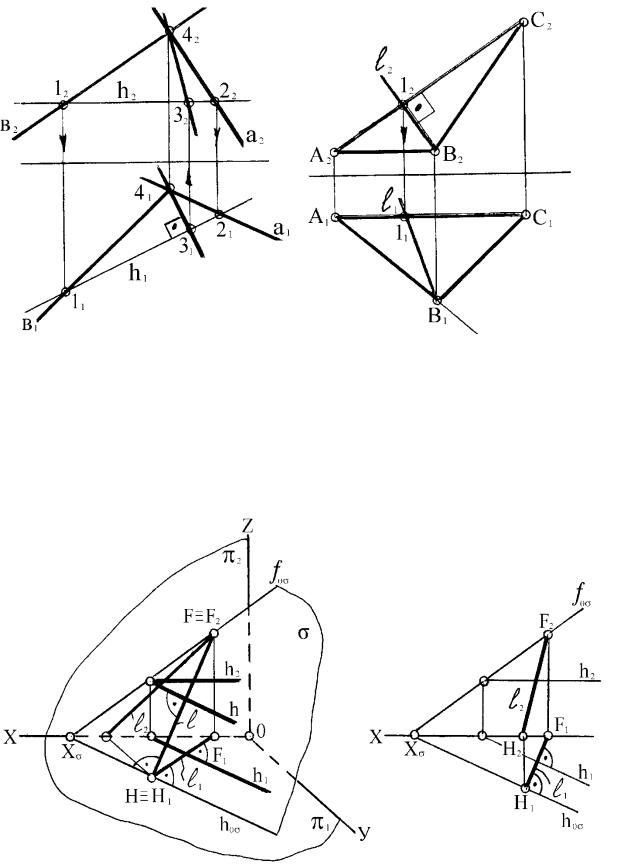
Рисунок 51 Рисунок 52
На рисунке 53 показано изображение линии наибольшего наклона (линии ската) плоскости, заданной следами. Горизонтальная проекция линии ската перпендикулярна горизонтальным проекциям горизонтали
(l1 h1 или
l1 h ),и ее следы принадлежат следам плоскости (Н h и F ).
Рисунок 53 Таким образом, чтобы построить линию наибольшего наклона
плоскости, необходимо в этой плоскости сначала провести прямую уровня. Тогда на основании свойства проецирования прямого угла
можно утверждать, что прямой угол, составленный линией наибольшего наклона с горизонталью (фронталью), на горизонтальную (фронтальную) плоскость проекций проецируется без искажения.
Через заданную точку плоскости можно провести лишь одну линию ската и одну линию наклона к фронтальной плоскости проекций.
5.4 Взаимное положение прямой линии и плоскости
Прямая линия относительно плоскости может занимать два положения: принадлежать плоскости или пересекать ее.
Частными случаями пересечения могут быть: параллельность – пересечение прямой с плоскостью в бесконечности и перпендикулярность – пересечение прямой с плоскостью под углом 90о. При определении взаимного положения прямой линии с плоскостью используется следующие положения, известные из геометрии:
-через одну точку пространства можно провести бесчисленное количество прямых линий;
-две точки однозначно определяют положение прямой линии;
-если две точки прямой принадлежат плоскости, то прямая линия принадлежит этой плоскости;
-прямая линия параллельна плоскости, если она параллельна какой-либо прямой этой плоскости;
-если прямая линия перпендикулярна к двум непараллельным прямым плоскости, то она перпендикулярна к этой плоскости;
-через одну прямую линию можно провести бесчисленное количество плоскостей;
-две плоскости пересекаются по единственной прямой
линии.
Если на чертеже непосредственно нельзя установить взаимного положения прямой линии и плоскости, то прибегают к некоторым вспомогательным построениям, в результате которых от вопроса о взаимном положении прямой и плоскости переходят к вопросу о взаимном положении данной прямой и некоторой вспомогательной прямой. Указанный прием определения взаимного положения прямой линии и плоскости заключается в следующем:
-через данную прямую проводят вспомогательную плоскость и строят линию пересечения этой плоскости с данной плоскости;
-устанавливают взаимное положение плоскостей. Найденное положение определяет взаимное положение данных прямой и плоскости.
5.4.1 Прямая параллельная плоскости

Для того чтобы прямая была параллельна данной плоскости, необходимо, чтобы она была параллельна какой-либо прямой линии, лежащей в этой плоскости. В плоскости можно провести неограниченное число прямых линий параллельных плоскости.
Если задана плоскость (АВС) и точка D, то, чтобы провести
через
точку D прямую линию DЕ параллельно данной плоскости (рисунок 54, а), необходимо провести ее проекции параллельно одноименным проекциям одной из сторон треугольника АВС либо прямой линии, лежащей в этой плоскости. На рисунке 54, а D2Е2 А2В2 и D1Е1 А1В1,
следовательно, DЕ (АВС). На рисунке 54, б показана прямая линия,
параллельная плоскости, заданной следами: l а, а а .
а) |
б) |
Рисунок 54
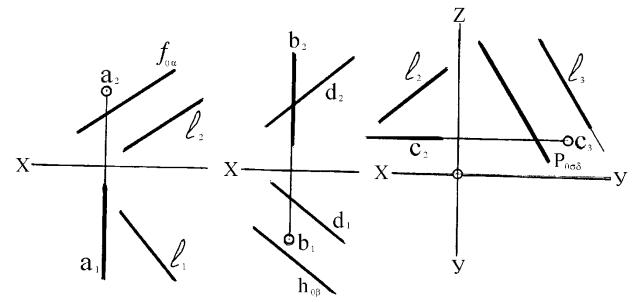
Если плоскость является проецирующей, то любая одноименно проецирующая прямая параллельна этой плоскости, потому что в плоскости всегда можно найти одноименно проецирующую прямую. На
рисунке 55 изображены плоскости: 2, 1, 3. Этим плоскостям будут параллельны прямые а (а 2); b (b 1); с(с 3). Любая прямая l, у которой l2 (l1 – произвольно), будет
параллельна плоскости .
Аналогично d1 d ; е3 е .
а) |
б) |
в) |
Рисунок 55
5.4.2 5.4.2 Пересечение прямой линии с плоскостью
Если прямая линия не параллельна плоскости, то она пересекается с плоскостью. Построение точки пересечения прямой линии с плоскостью является одной из основных позиционных задач начертательной геометрии. Позиционными называют задачи,
связанные с решением на комплексном чертеже вопросов взаимного расположения геометрических образов. Прямая линия, пересекающая плоскость, имеет с ней единственную общую собственную точку.
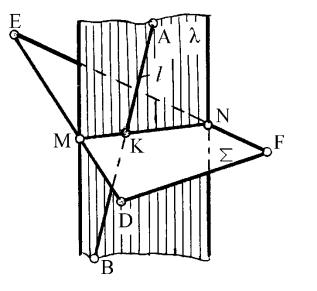
В решении задачи используют проецирующую плоскость как секущую вспомогательную плоскость. Рассмотрим схему решения задачи на определение точки пересечения прямой l (АВ)с плоскостью (DEF). Задача решается в следующей последовательности (рисунок 56):
|
1. |
|
|
1 |
. |
Через прямую l |
(АВ)проводим проецирующую плоскость |
||
(горизонтально |
– |
либо фронтально-проецирующую), |
т.е. |
|
l 1. |
|
|
|
|
|
2. |
|
|
2 |
. |
Определяем |
линию пересечения заданной плоскости |
с |
|
вспомогательной плоскостью ; она определяется по точкам M и N пересечения прямых линий DE и EF плоскости с плоскостью
:
M = DE ; N = EF ; MN= . |
|
3. |
3 |
. Определяем точку K пересечения данной прямой l(AB)с линией |
|
пересечения плоскостей и , то есть K |
= MN l. Точка K, |
общая для прямойlи плоскости , является искомой точкой пересечения прямой линии с плоскостью.
Рисунок 56
Рассмотрим решение этой задачи на комплексном чертеже (рисунок 57). Пусть дана плоскость общего положения (АВС) и
прямая a. Определим
точку пересечения прямой линии с плоскостью.
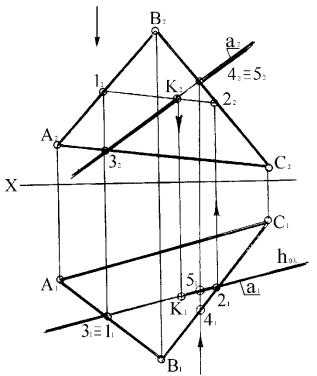
Рисунок 57 |
|
Проведем горизонтально-проецирующую плоскость : |
a и |
построим линию 12 пересечения плоскостей – заданной и |
|
вспомогательной. Обе прямые линии a и12 инциндентны плоскости , следовательно, их горизонтальные проекции совпадают.
В пересечении 1222 с a2 отметим точку K2, а затем найдем K1. Точка K
есть точка пересечения прямой линии a сплоскостью (АВС). Видимость прямой линии и плоскости относительно
горизонтальной плоскости проекций определяется с помощью
горизонтально-конкурирующих точек 1 |
и 3, а видимость относительно |
|||
фронтальной плоскости |
проекций |
– |
с помощью |
фронтально- |
конкурирующих точек 4 и 5. |
|
|
|
|
Определим видимые |
и невидимые |
(относительно |
плоскостей |
|
проекций) отрезки прямой линии a,применяя способ «конкурирующих» точек – точек принадлежащих их общему проецирующему лучу. Если смотреть по направлению проецирующего луча, то можно увидеть ту из конкурирующих точек, которая наиболее удалена от плоскости проекций (наиболее близко расположена к наблюдателю).
На горизонтально-проецирующем луче 13 находятся точки 1 и 3, принадлежащие прямым линиям АВ и a. Точка 1 принадлежит стороне
АВ треугольника АВС, а точка 3 – прямой a. По фронтальным проекциям 12 и 32 этих точек устанавливаем, что одна из них (точка 1) выше, чем другая (точка 3). Следовательно, на участке К3 прямая линия
a (если смотреть на горизонтальную плоскость проекций 1) находится
